Perihelio
El perihelio (de περί [perí], ‘en torno a’ o ‘alrededor de’, y ἥλιος [hélios], ‘Sol’) es el punto más cercano de la órbita de un cuerpo celeste alrededor del Sol.[1] Es el opuesto al afelio[1] (punto más lejano)[2] y se representa por . Si es el semieje mayor y es la excentricidad, entonces .
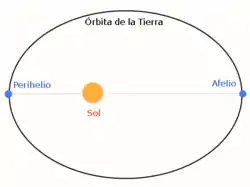 |
| Esquema de la órbita de la Tierra, con los puntos de afelio y perihelio. |
Tal como establece la segunda de las leyes de Kepler, la velocidad de traslación del cuerpo celeste es máxima en el perihelio y se puede calcular conociendo el semieje mayor de la órbita, la excentricidad , la masa del Sol y la constante de gravitación universal mediante la expresión :[3]
Como el semieje mayor de la órbita de la Tierra es a = 149,60 millones de km y la excentricidad es e = 0,01671 a principios del mes de julio (generalmente, el día 4), en el afelio, la Tierra dista 152,10 millones de kilómetros del Sol, mientras que a comienzos de enero (también el día 4), en el perihelio o punto de su órbita elíptica más cercano al Sol, la distancia es de q = 147,10 millones de km.[n 1] Actualmente el perihelio ocurre alrededor de 15 días después del solsticio de diciembre.
Movimiento de precesión
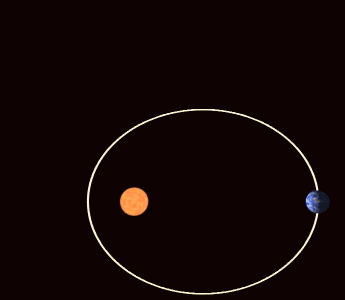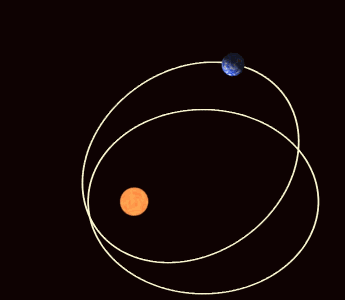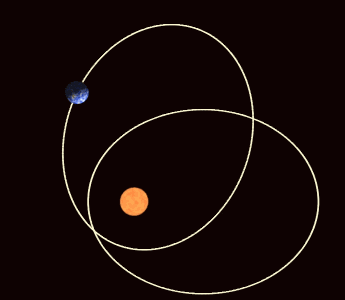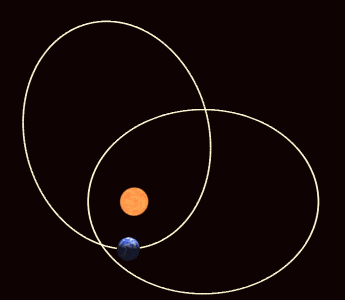
En el movimiento de traslación, la tierra describe una elipse en torno al Sol, que ocupa uno de los focos de dicha elipse, pero el otro foco no es estático, también gira lentamente un pequeño ángulo de 3,84 arcosegundos por siglo, alrededor del Sol, en el mismo sentido de la órbita y este giro del foco libre de la elipse se conoce como precesión apsidial o precesión o avance del perihelio, que es el momento de menor distancia de la Tierra al Sol. Lógicamente el afelio, o momento de mayor distancia de la Tierra al Sol, también sufre este avance, que, aun siendo angularmente igual, tangencialmente es mayor todavía. Este movimiento tiene un período de unos 34 285 714 años.
Véase también
Notas
- A principios de enero (generalmente, el día 4), en astromia.com
Referencias
- Materiales Didacticos N0.2. Andres Bello. Consultado el 6 de enero de 2020.
- Sixto Casado, Rafael (1863). Elementos de cosmografía.
- La web de Física. «Cálculo de la velocidad en órbitas elípticas». Consultado el 13 de septiembre de 2017.