Polígono mágico
Un polígono mágico es un grafo mágico poligonal con números enteros en sus vértices.
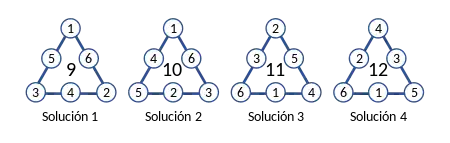
Polígono mágico perimetral
Un polígono mágico, también llamado polígono mágico perimetral,[1][2] es un polígono con números enteros en sus lados que suman una constante mágica.[3][4] Además, se debe cumplir la condición de que deben usarse los enteros positivos (del 1 al N).
Para formar un polígono mágico, se deben disponer estos números en el perímetro de un polígono de k lados, de forma que si se suman en cada lado (incluyendo los dos vértices) siempre deben dar la misma constante.[1] Los polígonos mágicos son una generalización de otras formas mágicas,[5] como los triángulos mágicos.[6]
Polígonos mágicos con un punto central

Victoria Jakicic y Rachelle Bouchat definieron los polígonos mágicos como polígonos regulares de n lados con 2n+1 nodos (uno de ellos, un nodo central), de forma que la suma de cada tres nodos (cada par diagonalmente opuesto, más el central) es la misma. En su definición, un cuadrado mágico de 3×3 se puede ver como un 4-ágono mágico. No hay polígonos mágicos impares con esta definición (dado que los nodos no pueden estar diagonalmente opuestos en este caso).[7]
Polígonos mágicos concéntricos y polígonos mágicos degenerados
Danniel Dias Augusto y Josimar da Silva definieron el polígono mágico P(n,k) como un conjunto de nodos, de los cuales son los vértices de los polígonos regulares que rodean concéntricamente al punto central, de forma que cada lado de cada polígono y cada diagonal del mayor polígono contiene nodos (incluidos los vértices que los delimitan). Lógicamente, tanto n como k deben ser números pares. En esta definición, los polígonos mágicos de Victoria Jakicic y Rachelle Bouchat pueden verse como polígonos mágicos de la forma P(n,2). También definieron polígonos mágicos degenerados, con los polígonos creciendo en capas sucesivas alrededor de un vértice (para n impar).[8]
Véase también
Referencias
- «Perimeter Maghic Polygons». www.trottermath.net. Archivado desde el original el 12 de enero de 2018. Consultado el 12 de febrero de 2017.
- «Perimeter Magic Polygon >k=3». www.magic-squares.net. Consultado el 12 de febrero de 2017.
- Staszkow, Ronald (1 de mayo de 2003). Math Skills: Arithmetic with Introductory Algebra and Geometry (en inglés). Kendall Hunt. p. 199. ISBN 9780787292966. «Magic polygon math. »
- Bolt, Brian (9 de abril de 1987). Even More Mathematical Activities (en inglés). Cambridge University Press. ISBN 9780521339940.
- Croft, Hallard T.; Falconer, Kenneth; Guy, Richard K. (6 de diciembre de 2012). Unsolved Problems in Geometry: Unsolved Problems in Intuitive Mathematics (en inglés). Springer Science & Business Media. ISBN 9781461209638.
- Heinz, Harvey D. «Perimeter Magic Triagonals». recmath.org. Consultado el 12 de febrero de 2017.
- Jakicic, Victoria; Bouchat, Rachelle (2018). «Magic Polygons and Their Properties». .
- Danniel Dias Augusto; Josimar da Silva Rocha (2019). «Magic Polygons and Degenerated Magic Polygons: Characterization and Properties». .