Poliedro prismático uniforme
En la geometría, un poliedro prismático uniforme o regular es un poliedro uniforme con simetría diedral. Estos existen en dos familias infinitas, los prismas uniformes y los antiprismas uniformes. Todos tienen sus vértices en planos paralelos, por lo que se denominan prismatoides.
Tipos
| Grupo de simetría | Convexo | Formas estrelladas | ||||||
|---|---|---|---|---|---|---|---|---|
| D2d, [2+,2], (2*2) |  3.3.3 | |||||||
| D3h, [2,3], (*223) |  3.4.4 | |||||||
| D3d, [2+,3], (2*3) |  3.3.3.3 | |||||||
| D4h, [2,4], (*224) |  4.4.4 | |||||||
| D4d, [2+,4], (2*4) |  3.3.3.4 | |||||||
| D5h, [2,5], (*225) |  4.4.5 |
 4.4.5⁄2 |
 3.3.3.5⁄2 | |||||
| D5d, [2+,5], (2*5) |  3.3.3.5 |
 3.3.3.5⁄3 | ||||||
| D6h, [2,6], (*226) |  4.4.6 | |||||||
| D6d, [2+,6], (2*6) | 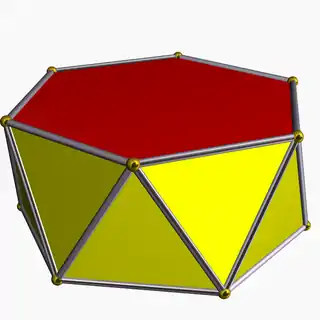 3.3.3.6 | |||||||
| D7h, [2,7], (*227) |  4.4.7 |
 4.4.7⁄2 |
 4.4.7⁄3 |
 3.3.3.7⁄2 |
 3.3.3.7⁄4 | |||
| D7d, [2+,7], (2*7) |  3.3.3.7 |
 3.3.3.7⁄3 | ||||||
| D8h, [2,8], (*228) |  4.4.8 |
 4.4.8⁄3 | ||||||
| D8d, [2+,8], (2*8) |  3.3.3.8 |
 3.3.3.8⁄3 |
 3.3.3.8⁄5 | |||||
| D9h, [2,9], (*229) |  4.4.9 |
 4.4.9⁄2 |
 4.4.9⁄4 |
 3.3.3.9⁄2 |
 3.3.3.9⁄4 | |||
| D9d, [2+,9], (2*9) |  3.3.3.9 |
 3.3.3.9⁄5 | ||||||
| D10h, [2,10], (*2.2.10) | 4.4.10 |
 4.4.10⁄3 | ||||||
| D10d, [2+,10], (2*10) |  3.3.3.10 |
 3.3.3.10⁄3 | ||||||
| D11h, [2,11], (*2.2.11) |  4.4.11 |
 4.4.11⁄2 |
 4.4.11⁄3 |
 4.4.11⁄4 |
 4.4.11⁄5 |
 3.3.3.11⁄2 |
 3.3.3.11⁄4 |
 3.3.3.11⁄6 |
| D11d, [2+,11], (2*11) | 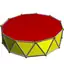 3.3.3.11 |
 3.3.3.11⁄3 |
 3.3.3.11⁄5 |
 3.3.3.11⁄7 | ||||
| D12h, [2,12], (*2.2.12) |  4.4.12 |
 4.4.12⁄5 | ||||||
| D12d, [2+,12], (2*12) |  3.3.3.12 |
 3.3.3.12⁄5 |
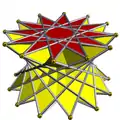 3.3.3.12⁄7 | |||||
| ... | ||||||||
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.