Polinomios de Bernoulli
En matemáticas, los polinomios de Bernoulli se definen mediante la función generatriz:
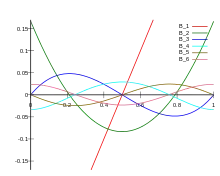
Polinomios de Bernoulli
Aparecen en el estudio de numerosas funciones especiales, en particular de la función zeta de Riemann y de la función zeta de Hurwitz. Los números de Bernoulli son los términos independientes de los polinomios correspondientes, i.e., .
La identidad nos permite dar una forma cerrada de la suma
Los polinomios de Bernoulli se pueden calcular a partir de la siguiente fórmula:
Expresión explícita de polinomios de menor grado
Los primeros Polinomios de Bernoulli son:
- .
- .
- .
- .
Véase también
Referencias
- Zwillinger, D. CRC Standard Mathematical Tables and Formulae, CRC Press, 2003. ISBN 1584882913.
Enlaces externos
- Weisstein, Eric W. «Bernoulli Polynomial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.