Pozo gravitatorio
Un pozo gravitatorio o pozo de gravedad es un modelo conceptual del campo gravitacional que rodea un cuerpo en el espacio: cuanto más masivo es el cuerpo, más intensa y mayor es la extensión de la gravedad asociada con él. El Sol es muy masivo, en relación con otros cuerpos en el Sistema solar, por lo que el pozo de gravedad correspondiente que lo rodea parece «profundo» y de gran alcance. Los pozos de gravedad de los asteroides y lunas pequeñas, a la inversa, a menudo se representan como muy superficiales. Cualquier cosa en la superficie de un planeta o luna se considera que está en la parte inferior del pozo gravitatorio de ese cuerpo celeste, por lo que escapar de los efectos de la gravedad de dicho planeta o luna (para ingresar al espacio exterior) a veces se denomina salir del pozo gravitatorio. Cuanto más profundo es un pozo de gravedad, más energía se debe usar para escalar el pozo y alcanzar la velocidad de escape que hace posible acceder al espacio exterior.[1]
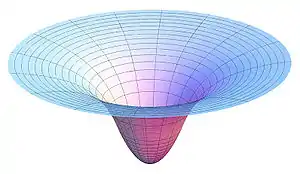
En astrofísica, un pozo de gravedad es específicamente el campo producido por el potencial gravitatorio alrededor de un cuerpo masivo. Otros tipos de pozo de potencial incluyen pozos de potencial eléctrico y magnético. Los modelos físicos de pozos de gravedad a veces se usan para ilustrar conceptos de astrodinámica.
No deben ser confundidos con los agujeros negros, un caso extremo de física relativista en el marco de la relatividad general. Ambos conceptos están claramente separados y no guardan una relación directa entre sí.
Detalles

Si G es la constante de gravitación universal universal (G = 6.67 × 10−11 m³ kg−1 s−2), el potencial gravitatorio externo de un cuerpo de masa esféricamente simétrico M se da por la fórmula:
En la figura se muestra un gráfico de esta función en dos dimensiones. Esta trama se ha completado con un potencial interior proporcional a |x|2, que corresponde a un objeto de densidad uniforme, pero este potencial interior es generalmente irrelevante, ya que la órbita de las partículas materiales no pueden cruzarse con el cuerpo.
La función potencial tiene una sección transversal hiperbólica; la pronunciada depresión en el centro del campo potencial es el origen del nombre de «pozo de gravedad». Un agujero negro no tendría esta caída de «cierre» debido a que su tamaño solo está determinado por su horizonte de sucesos.
Modelo físico de un pozo de gravedad
En un campo gravitacional uniforme, el potencial gravitatorio en un punto es proporcional a su altura (por ejemplo, como pasa en la cercanía de la superficie de la Tierra). Por lo tanto, si el gráfico de un potencial gravitacional Φ(x, y) se construye como una superficie física y se coloca en un campo gravitatorio uniforme para que el campo real apunte en la dirección -Φ, entonces cada punto de la superficie tendrá un potencial gravitatorio real proporcional al valor de Φ en ese punto. Como resultado, un objeto restringido a moverse sobre la citada superficie tendrá aproximadamente la misma ecuación de movimiento que un objeto que se mueve en el campo potencial Φ en sí mismo. Los pozos de gravedad construidos según este principio se pueden encontrar en muchos museos de ciencia.[1]
Hay varias fuentes de inexactitud en este modelo:
- La fricción entre el objeto y la superficie no tiene analogía en el vacío. Este efecto se puede reducir usando una bola rodante en lugar de un bloque deslizante.
- El movimiento vertical del objeto aporta energía cinética que no tiene analogía. Este efecto se puede reducir haciendo que la gravedad sea menos profunda (es decir, eligiendo un factor de escala más pequeño para el eje Φ).
- La energía cinética de rotación de una bola rodante no tiene analogía. Este efecto se puede reducir al concentrar la masa de la bola cerca de su centro, de modo que el momento de inercia sea pequeño en comparación con mr2.
- El centro de masa de una bola no se encuentra en la superficie sino a una distancia fija r (determinada por el radio de la bola), que modifica su energía potencial en una cantidad que depende de la pendiente de la superficie en ese punto. Para las bolas de un tamaño fijo, este efecto puede eliminarse construyendo la superficie de modo que el centro de la bola se corresponda con la gráfica de Φ, en lugar del punto de contacto entre la bola y la superficie.
El modelo de la lámina elástica
Considérese una lámina elástica idealizada, suspendida en un campo gravitatorio uniforme y perpendicular a la lámina. En equilibrio, la tensión elástica en cada punto de la lámina debe ser igual y opuesto a la atracción gravitatoria en ese punto de la lámina; es decir,
donde k es el módulo de elasticidad del material de la lámina, h(x) indica el valor del desplazamiento vertical hacia arriba (se supone que es pequeño) de un punto de la lámina, g es la fuerza del campo gravitacional, y ρ(x) es la densidad de la lámina. La densidad puede considerarse como intrínseca a la hoja o como perteneciente a los objetos que descansan en la parte superior de la hoja. Esta condición de equilibrio es idéntica en forma a la Ecuación de Poisson gravitacional:
donde Φ(x) es el potencial gravitacional y ρ(x) es la densidad del material. Así, para una primera aproximación, un objeto masivo colocado sobre una lámina de caucho deformará la lámina en un pozo gravitatorio correctamente formado, y (como en el caso anterior), y un segundo objeto de prueba colocado cerca del primero gravitará hacia él en una aproximación de la ley de fuerzas correcta.[2]
Pozos de gravedad y relatividad general
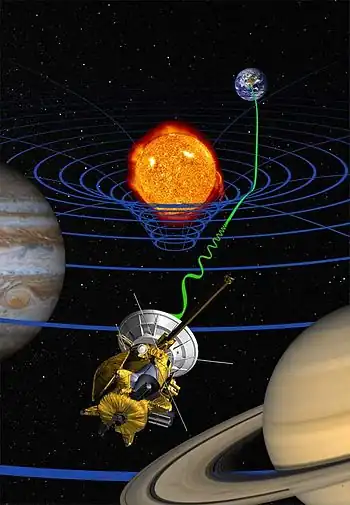
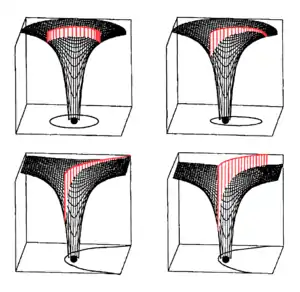
Tanto el pozo de gravedad rígido como el modelo de lámina elástica son frecuentemente identificados erróneamente como modelos de la relatividad general, debido a un parecido accidental con ciertos diagramas relativistas generales, y quizás al empleo de Einstein del concepto de curvatura gravitacional capaz de desviar la trayectoria de la luz que describió como una predicción de la relatividad general. Un diagrama frecuente en los libros de texto, la inclusión de una porción ecuatorial constante de la métrica de Schwarzschild en el espacio euclidiano tridimensional, se asemeja superficialmente a un pozo de gravedad. Sin embargo, los diagramas de inclusión difieren conceptualmente de los pozos de gravedad.
Esta inclusión significa la modificación de la trama espacial uniforme euclidea, mientras que una retícula representando el potencial gravitatorio tiene una dirección particular («hacia abajo») con una interpretación física completamente diferente. Dar la vuelta a la superficie rígida que representa un pozo de gravedad, equivale a cambiar el signo del potencial de la fuerza de atracción, que pasaría a ser una fuerza de repulsión. Sin embargo, dar la vuelta a una inserción Schwarzschild rotándola, no tiene ningún efecto, ya que no modifica su geometría intrínseca. Además, las geodésicas que siguen a través de la superficie de Schwarzschild se doblarían hacia la masa central como una bola rodando en un pozo de gravedad, pero por razones completamente diferentes. No existe una analogía de la incrustación de Schwarzschild para un campo repulsivo. Aunque dicho campo se modela en la relatividad general, su geometría espacial no se puede incluir en tres dimensiones.
La incrustación de Schwarzschild comúnmente se dibuja con una sección transversal hiperbólica como el pozo potencial, pero de hecho tiene una sección transversal parabólica que, a diferencia del pozo de gravedad, no se acerca a un plano asintótico (véase el paraboloide de Flamm).
Véase también
- Efecto geodésico
- Esfera de influencia
- Vórtice
Referencias
- Keith J. Mirenberg. «INTRODUCTION TO GRAVITY-WELL MODELS OF CELESTIAL OBJECTS» (en inglés). Consultado el 19 de septiembre de 2018.
- Robert F. Schuyler (2009). Time. Dorrance Publishing. pp. 53 de 356. ISBN 9781434991157. Consultado el 19 de septiembre de 2018.