Principio isolobal

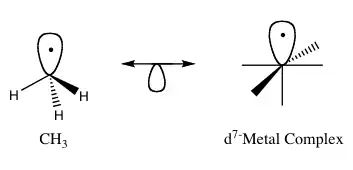
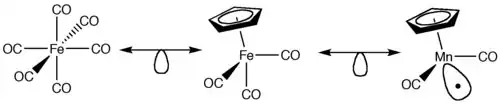
El principio isolobal (más formalmente conocido como analogía isolobal) es una estrategia utilizada en química organometálica para relacionar la estructura de fragmentos moleculares inorgánicos y orgánicos para pronosticar propiedades de enlace de compuestos organometálicos.[1] Roald Hoffmann Describió fragmentos moleculares como isolobales solo "si el número, propiedades de simetría, forma y energía aproximadas de los orbitales frontera y el número de los electrones en ellos son similares– no idénticos, pero similares."[2] Uno puede pronosticar la vinculación y reactividad de una especie poca conocida a partir de una especie mejor conocida si los dos fragmentos moleculares tienen orbitales frontera similares, el orbital molecular más alto ocupado por sus siglas en inglés (HOMO) y el orbital molecular más bajo sin ocupar (LUMO). Los compuestos isolobales son equivalentes a los compuestos isoelectrónicos que comparten el mismo número de electrones de valencia y estructura.Las estructuras isolobales se pueden representar gráficamente con los pares isolobales conectados a través de una flecha de doble punta con un medio orbital abajo, como se muestra en la Figura 1.

Figura 1: ejemplo Básico de la analogía isolobal.

Hoffmann presentó su trabajo respecto a la analogía isolobal, cuando se le otorgó el premio Nobel en Química en 1981, el cual compartiría con Kenichi Fukui.[3] Por sus teorías (desarrolladas independientemente) respecto a al desarrollo y dirección de reacciones químicas.

Construcción de fragmentos isolobales

Para empezar a generar un fragmento isolobal, la molécula necesita seguir ciertos criterios.[4] Las moléculas basadas alrededor de elementos de grupo principal tendrán que cumplir la regla del octeto cuando todos los orbitales moleculares (OMs), de enlace y no-enlace estén llenos y todos los OMs de anti enlace estén vacíos. Por ejemplo el metano es una molécula sencilla de la cual formar un fragmento de grupo principal. La extracción de un átomo de hidrógeno de metano genera un radical de metilo. La molécula retiene su geometría molecular como los orbitales frontera en la dirección del átomo de hidrógeno que falta. Extracción consecutiva de hidrógeno cae como resultado en la formación de un orbital de frontera secundario. Este proceso puede ser repetido hasta que solo quede un enlace al átomo central de la molécula. La Figura 2 demuestra este ejemplo de generación paso-por-paso de fragmentos isolobales.

Figura 2: Construcción de orbitales frontera a partir de metano.

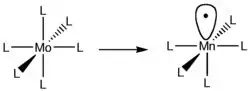
Los fragmentos isolobales de complejos octaédricos, como ML6, se pueden crear de una forma similar. Complejos de metales de transición inicialmente tendrían que satisfacer la regla de dieciocho electrones, no tener carga neta, y su ligandos deben ser donantes de dos electrones (Bases de Lewis). Consiguientemente, el centro de metal para el ML6 tiene que ser d6 como punto de partida. La extracción de un ligando es análoga a la extracción de hidrógeno de metano en el ejemplo anterior que resulta en un orbital frontera, el cual señala hacia el ligando removido. La remoción de un enlace entre el centro de metal y un ligando resulta en un complejo radical ML5-. Para satisfacer los criterios de carga cero, el centro del metal tiene que ser cambiado. Por ejemplo, un complejo MoL6 es d6 y neutro. Sacando un ligando para formar el primer orbital frontera resultaría en un complejo MoL5− porque el Mo ha ganado un electrón adicional que lo vuelve d7. Para remediar esto, Mo puede ser intercambiado por Mn, el cual formaría un complejo neutral d7 en este caso, como se muestra en la Figura 3. Esta tendencia puede continuar hasta que solo quede un ligando coordinado al centro del metal.

Figura 3: Producción de un orbital de frontera en un complejo octaédrico. Ya que el proceso no produce carga, el centro del metal debe cambiar de Mo d6 a Mn d7 para mantener su carga neutra.

Relación entre fragmentos tetraédricos y octaédricos
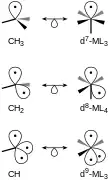
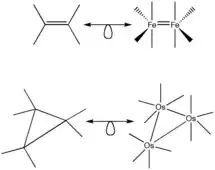
Figura 4: fragmentos Isolobales de geometrías tetraédricas y octaédricas.

Los fragmentos Isolobales de moléculas tetraédricas y octaédricas pueden ser relacionados. Estructuras con el mismo número de orbitales frontera son isolobales una con la otra. Por ejemplo, el metano con dos átomos de hidrógeno removidos, CH2 es isolobal a un complejo ML4 d8 formado de un complejo octaédrico inicial (Figura 4). Analogías similares pueden ser hechas entre cualquier CH3 y ML5 d7 o CH y ML3 d9.

Dependencia a la teoría de OM

Cualquier clase de molécula saturada puede ser el punto de partida para generar fragmentos isolobales .[5][6] Los OM de enlace y no enlace de las moléculas debem estar llenos así como los OM de antienlace deben estar vacíos. Con cada generación consecutiva de un fragmento isolobal, los electrones son removidos de los obitales de enlace y un orbital de frontera es creado. Los orbitales de frontera están a un nivel de energía mayor que los OM de enlace y no enlace. Cada orbital de frontera contiene un electrón. Por ejemplo, considere la Figura 5, el cual muestra la producción de orbitales frontera en moléculas tetraédricas y octaédricas.

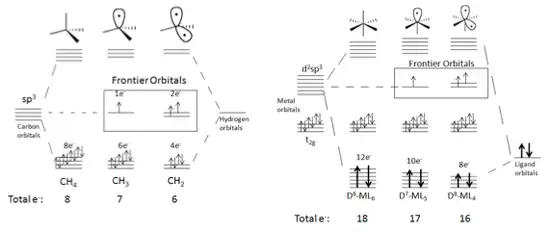
Figura 5: Representación de un esquema de orbitales Moleculares de orbitales frontera en metano y un complejo metálico complejo básico ML6.

Visto superficialmente, cuándo un fragmento se forma de CH4, uno de los orbitales híbridos sp3 relacionados en el enlace se vuelve un orbital de frontera de no enlace ocupado únicamente por un electrón. El incremento en el nivel de energía del orbital frontera también se muestra en la figura. De modo parecido cuándo se inicia con un complejo de metal como ML6-d6, los orbitales híbridos d2sp3 son afectados. Además los orbitales metálicos de no enlace t2g permanecen sin alteraciones.

Extensiones de la analogía

La analogía isolobal tiene aplicaciones más allá de complejos octaédricos sencillos. Puede ser utilizado con una variedad de ligandos, especies cargadas y complejos no octaédricos.

La extensión de la analogía podrían numerarse de la siguiente forma:

  1. La definición isolobal puede extenderse a los fragmentos isoelectrónicos con números de coordinación similares.
  2. La ganancia o pérdida de electrones de dos fragmentos isolobales crea más fragmentos isolobales.
  3. Otras moléculas donadoras de 2 electrones se tratan de igual forma que CO:**
  4. Para los ligandos n5-C5H5 y n6-C6H6 se considera que ocupan tres sitios de coordinación y que son donadores de 6 electrones.
  5. Los fragmentos octaédricos de fórmula MLn (Dónde M tiene una configuración dx) son isolobales con fragmentos cuadrado planos de fórmula MLn-2 (Donde M tiene una configuración dx+2 y L is un donador de dos electrones).[7]

Ligandos

Los ligandos usados típicamente en la analogía isolobal, son donadores de dos electrones, como lo son las fosfinas, halógenos o carbonilos. Sin embargo , otros tipos de ligandos puede ser empleados. Si los ligandos donan pares múltiples de electrones, ocuparán sitios de coordinación múltiple. Por ejemplo, el anión cyclopentadienilo es un donador de seis electrones, así que ocupa tres sitios de coordinación. Ligandos Polidentados también pueden ser utilizados en la analogía, como etilendiamina, un ligando bidentado, o trietilenotetramina, un ligando tetradentado.

Figura 6: Ejemplo de cyclopentadieno, un ligando de coordinación múltiple en analogía isolobal.

Fragmentos Isoelectronicos

La analogía isolobal también puede ser utilizada con fragmentos isoelectrónicos con el mismo número de coordinación, el cual permite que la especie cargada sea considerada. Por ejemplo, Re(CO)5 es isolobal con CH3 y por tanto, [Ru(CO)5]+ y [Mo(CO)5]− es también son isolobales con CH3. Cualquiera complejo metálico de 17 electrones sería isolobal en este ejemplo.

En un sentido similar, la adición o extracción de electrones de dos fragmentos isolobales resultan en dos nuevos fragmentos isolobales. Ya que Re(CO)5 es isolobal con CH3, [Re(CO)5]+ es isolobal con CH3+.[8]

Complejos no octaédricos
Figura 7: relación isolobal entre complejos octaédricos y complejos cuadrado planos.
MLn

Octaédrico

 Cuadrado-plano

MLn-2

d6: Mo(CO)5 d8: [PdCl3]−
d8: Os(CO)4 d10: Ni(PR3)2
Figura 8: Ejemplos de formas no básicas en la analogía isolobal.

La analogía aplica a otras formas además de las geometrías tetraédricas y octaédricas. Las derivaciones utilizadas en la geometría octaédrica son válidas para casi todas las otras geometrías. La excepción es la geometría cuadrada plana ya que los complejos cuadrado-planos se rigen típicamente con la regla de 16 electrones.

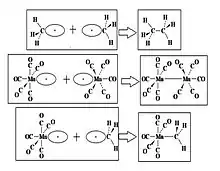
Figura 8.2: Formación de H3C—Mn(CO)5 a partir de Etano y (OC)5Mn—Mn(CO)5.

Estos fragmentos pueden ser combinados en moléculas: dos fragmentos CH3 de etano y dos fragmentos de Mn(CO)5 de un complejo formado (CO)5Mn-Mn(CO)5. Más adelante estos fragmentos orgánicos e inorgánicos pueden combinarse para conseguir un complejo H3C-Mn(CO)5. como se muestra en la figura 8.2[7]

Suponiendo que los ligandos actúan como donadores de dos electrones el centro metálico en las moléculas cuadradas planas es d8. Para relacionar un fragmento octaédrico, MLn, donde M tiene una configuración electrónica dx a un fragmento cuadrado-plano análogo, la fórmula MLn−2 dónde M tiene una configuración electrónica dx+2 tendría que ser la siguiente.

Otros ejemplos de la analogía isolobal en varias figuras y formas se muestran en la Figura 8.

Aplicaciones y ejemplos
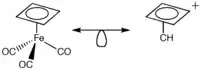
Figura 9: la relación Potencial basada en principios isolobales.

Usos de la analogía isolobal incluye proporcionar atajos o caminos cortos y fáciles para la comprensión de la estructura electrónica, prediciendo reactividad y mecanismos de reacción, y como método para clasificar moléculas.Las aplicaciones son generalmente usadas para hacer conexiones entre sistemas bien conocidos y los no tan conocidos. por ejemplo la posibilidad de que compuestos sin sintetizar puedan ser imaginados o visualizados se debe a los sistemas de los cuales se conoce mejor la conformación molecular.El principio isoloal no garantiza que estos productos sean capaces de sintetizar o reproducir, simplemente propone la posibilidad. Considerando la molécula Fe(CO)3 complejada con ciclobutadieno.[1] Fe(CO)3 es isolobal con CH+. Por lo tanto uno puede pronosticar que CH+ se coordinará con ciclobutadieno en una forma similar que Fe(CO)3 lo haría. Gracias a esto, la molécula C5H5+ puede ser mencionada y visualizada a pesar de las complicaciones actuales para sintetizarla.

Predecir la reactividad de los complejos también pueden ser logrado utilizando la analogía isolobal. De la simple visualización de dos radicales CH3 reaccionando para formar etano, uno puede basarse en el principio isolobal para predecir enlaces M-C o M-M como lo son (CH3)M(CO)5 y M2(CO)10, donde M es un d7.

Otra aplicación de la analogía isolobal es prediciendo los mecanismos de reacción.Como en otras aplicaciones, las reacciones de mecanismos de reacción bien conocidas pueden ayudar a predecir los caminos de reacción para reacciones poco conocidas. No hay límites en el potencial de comparaciones que pueden haber entre complejos orgánicos e inorgánicos. La analogía aplica en cualquier dirección, (de orgánicos a inorgánicos y viceversa o dentro de la misma clasificación (p.ej. de orgánico a orgánico)

Arteaga-Müller et al. Utilizaron esta analogía para relacionar complejos imido de medio sándwich con complejos isoelectrónicos de diciclopentadienilo.[9] La relación isolobal del imido y de los ligandos de ciclopentadienilo fue la clave de la comparación. El estudio encontró que la reactividad de estos dos tipos de complejos era similar pero que sus capacidades catalíticas diferían en algunos aspectos. El estudio muestra que la analogía isolobal no hace predicciones perfectas entre dos fragmentos isolobales, justo como lo menciona Hoffman en su conferencia del Nobel.[1]

Wu Et al. Aplicaron la analogía isolobal para explorar la relación que envolvían estructuras, como las propiedades energéticas y magnéticas entre boro poliédrico y sus semejantes hidrocarbonos[10] Como se determinó en este estudio, a pesar de su isolobalidad, estos dos arreglos de moléculas tienen diferencias significativas en su energía de tensión.

Goldman y Tyler utilizaron el concepto de analogía isolobal para determinar el mecanismo más probable para la supresión de una reacción.[11] Uno de los productos de irradiación de CpW(CO)3Me en la presencia de PPh3 es CpW(CO)3−.El mecanismo de dicha reacción fue estudiado y teorizado para ser isolobal a la dismutación de dímeros de enlaces metal-metal los cuales implicaban electrones intermediarios de valencia 19. Las reacciones son compuestas de fragmentos isolobales y los intermediarios clave de cada reacción son isolobales. Por lo tanto los caminos de la reacción son mecánicamente isolobales.

Referencias
  1. Hoffmann, R. (1982).
  2. In reference 10 of his Nobel Prize acceptance speech, Hoffmann states that the term "isolobal" was introduced in reference 1e, "Elian, M., Chen, M. M.-L., Mingos, D. M. P. and Hoffmann, R., Inorg.
  3. "The Nobel Prize in Chemistry 1981: Kenichi Fukui, Roald Hoffmann". nobelprize.org.
  4. Department of Chemistry.
  5. Joan Ribas Gispert (2008).
  6. Shriver, D.F.; Atkins, P.; Overton, T.; Rourke, J.; Weller, M.; Armstrong, F. (2006).
  7. Miessler, G. L.; Tarr, D. A. (2008).
  8. Douglas, B.; McDaniel, D.; Alexander, J. (1994).
  9. Arteaga-Müller, R.; Sánchez-Nieves, J.; Ramos, J.; Royo, P.; Mosquera, M.E.G. (2008).
  10. Wu, H.; Win, X.; Xu, X.; Jiao, H.; Schleyer, P. V. R. (2005).
  11. Goldman, A. D.; Tyler, D. R. (1986).
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.