Problema de Weber
En geometría, el problema de Weber, llamado así por Alfred Weber, es uno de los problemas más famosos de localización industrial. Requiere encontrar un punto en el plano que minimice la suma de los costos de transporte desde este punto hasta n puntos de destino, donde los diferentes puntos de destino pueden estar asociados con diferentes costos por unidad de distancia.
El problema de Weber generaliza el concepto de mediana geométrica, que supone que los costos de transporte por unidad de distancia son los mismos para todos los puntos de destino, y el problema de calcular el Punto de Fermat, la mediana geométrica de tres puntos. Por esta razón, a veces se le llama problema de Fermat-Weber, aunque también se ha utilizado el mismo nombre para el problema de la mediana geométrica no ponderada. El problema de Weber es a su vez generalizado por el problema de atracción-repulsión, que permite que algunos de los costes sean negativos, por lo que algunos de los puntos deben estar a la mayor distancia posible.
Definición e historia de los problemas de Fermat, Weber y de atracción-repulsión
| Problema de Fermat | Problema de Weber | Problema de atracción-repulsión | |
|---|---|---|---|
| Primera formulación por | Fermat (antes de 1640) | Simpson (1750) | Tellier (1985) |
| Solución geométrica del problema del triángulo | Torricelli (1645) | Simpson (1750) | Tellier (2013) |
| Solución numérica directa del problema del triángulo | Tellier (1972) | Tellier (1972) | Tellier (1985) |
| Solución numérica iterativa del problema | Kuhn y Kuenne (1962) | Kuhn y Kuenne (1962) | Chen, Hansen, Jaumard y Tuy (1992) |
En el caso del triángulo, el problema de Fermat consiste en situar un punto D con respecto a tres puntos A, B y C de forma que se minimice la suma de las distancias entre D y cada uno de los otros tres puntos. Fue formulado por el famoso matemático francés Pierre de Fermat antes de 1640, y puede verse como el verdadero comienzo tanto de la teoría de la ubicación como de la economía espacial. Torricelli encontró una solución geométrica a este problema alrededor de 1645, pero aún no se disponía de una solución numérica directa más de 325 años después. Kuhn y Kuenne[1] encontraron una solución iterativa para el problema general de Fermat en 1962 y, en 1972, Tellier[2] encontró una solución numérica directa para el problema del triángulo de Fermat, que es trigonométrica. La solución de Kuhn y Kuenne se aplica al caso de polígonos que tienen más de tres lados, lo que no ocurre con la solución de Tellier por razones que se explican más adelante.
El problema de Weber consiste, en el caso del triángulo, en situar un punto D con respecto a tres puntos A, B y C de forma que se minimice la suma de los costes de transporte entre D y cada uno de los otros tres puntos. El problema de Weber es una generalización del problema de Fermat, ya que involucra fuerzas de atracción tanto iguales como desiguales (véase más abajo), mientras que el problema de Fermat solo trata con fuerzas de atracción iguales. Primero fue formulado y resuelto geométricamente en el caso del triángulo por Thomas Simpson en 1750.[3] Más tarde fue popularizado por Alfred Weber en 1909.[4] La solución iterativa de Kuhn y Kuenne encontrada en 1962, y la solución de Tellier encontrada en 1972 se aplican al problema del triángulo de Weber así como al de Fermat. La solución de Kuhn y Kuenne se aplica también al caso de polígonos que tienen más de tres lados.
En su versión más simple, el problema de atracción-repulsión consiste en ubicar un punto D con respecto a tres puntos A1, A2 y R de tal manera que las fuerzas de atracción ejercidas por los puntos A1 y A2, y la fuerza de repulsión ejercida por el punto R se cancelen unas a otras en el punto óptimo. Constituye una generalización de los problemas de Fermat y Weber. Fue formulado y resuelto por primera vez, en el caso del triángulo, en 1985 por Luc-Normand Tellier.[5] En 1992, Chen, Hansen, Jaumard y Tuy encontraron una solución al problema de Tellier para el caso de polígonos de más de tres lados.
Solución geométrica de Torricelli al problema del triángulo de Fermat
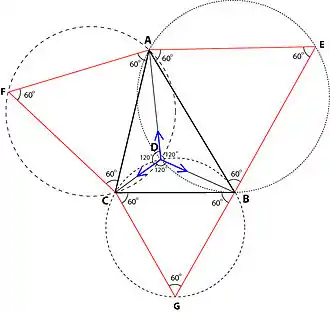
La solución geométrica de Evangelista Torricelli del problema del triángulo de Fermat se deriva de dos observaciones:
1– el punto D está en su ubicación óptima cuando cualquier movimiento significativo fuera de esa ubicación induce un aumento neto de la distancia total a los puntos de referencia A, B y C, lo que significa que el punto óptimo es el único punto donde un movimiento infinitesimal hacia uno de los tres puntos de referencia induce una reducción de la distancia a ese punto que es igual a la suma de los cambios inducidos en las distancias a los otros dos puntos; de hecho, en el problema de Fermat, la ventaja de reducir la distancia desde A en un kilómetro es igual a la ventaja de reducir la distancia desde B en un kilómetro o la distancia desde C en la misma longitud; en otras palabras, la actividad a ubicar en D es igualmente atraída por A, B y C;
2– según un importante teorema de la geometría euclidiana, en un cuadrilátero convexo inscrito en una circunferencia, los ángulos opuestos son suplementarios (es decir, su suma es igual a 180°); ese teorema también puede tomar la siguiente forma: si se corta un círculo con una cuerda AB, se obtienen dos arcos de círculo, denominados AiB y AjB; en el arco AiB, cualquier ángulo ∠AiB es el mismo para cualquier punto elegido i, y, en el arco AjB, todos los ángulos ∠AjB también son iguales para cualquier punto elegido j; además, los ángulos ∠AiB y ∠AjB son suplementarios.
Se puede demostrar que la primera observación implica que, en el punto óptimo, los ángulos entre las rectas AD, BD y CD deben ser iguales a 360° / 3 = 120°. Torricelli dedujo de esa conclusión que:
1– si cualquier triángulo ABD, cuyo ángulo ∠ADB es igual a 120°, genera un cuadrilátero ABDE convexo inscrito en una circunferencia, el ∠ABE un ángulo del triángulo ABE debe ser igual a (180° − 120°)= 60°;
2– una forma de determinar el conjunto de ubicaciones de D para las cuales el ángulo ∠ADB es igual a 120° es dibujar un triángulo ABE equilátero (porque cada ángulo de un triángulo equilátero es igual a 60°), donde E está ubicado fuera del triángulo ABC, y se dibuja un círculo alrededor de ese triángulo; entonces todos los puntos D’ de la circunferencia de ese círculo que están dentro del círculo ABC son tales que el ángulo ∠AD’B es igual a 120°;
3– el mismo razonamiento se puede hacer con respecto a los triángulos ACD y BCD;
4– esto lleva a trazar otros dos triángulos equiláteros ACF y BCG, donde F y G están ubicados fuera del triángulo ABC, así como otros dos círculos alrededor de estos triángulos equiláteros, y determinar la ubicación donde los tres círculos se cortan; en esa ubicación, los ángulos entre las rectas AD, BD y CD son necesariamente iguales a 120°, lo que prueba que es la ubicación óptima.
Solución geométrica de Simpson al problema del triángulo de Weber

La solución geométrica de Simpson del llamado “problema del triángulo de Weber” (que fue formulado por primera vez por Thomas Simpson en 1750) se deriva directamente de la solución de Torricelli. Simpson y Weber destacaron el hecho de que, en un problema de minimización total del transporte, la ventaja de acercarse a cada punto de atracción A, B o C depende de lo que se lleve y de su costo de transporte. En consecuencia, la ventaja de acercarse un kilómetro a A, B o C varía, y los ángulos ∠ADB, ∠ADC y ∠BDC ya no necesitan ser iguales a 120°.
Simpson demostró que, del mismo modo que en el caso del problema del triángulo de Fermat, los triángulos construidos ABE, ACF y BCG eran equiláteros porque las tres fuerzas de atracción eran iguales, en el caso del problema del triángulo de Weber, los triángulos construidos ABE, ACF y BCG , donde E, F y G se ubican fuera del triángulo ABC, deben ser proporcionales a las fuerzas de atracción del sistema de ubicación.
La solución es tal que:
1– en el triángulo construido ABE, el lado AB es proporcional a la fuerza de atracción Cw que apunta hacia C, el lado AE es proporcional a la fuerza de atracción Bw que apunta hacia B, y el lado BE es proporcional a la fuerza de atracción Aw que apunta hacia A;
2– en el triángulo construido BCG, el lado BC es proporcional a la fuerza de atracción Aw que apunta hacia A, el lado BG es proporcional a la fuerza de atracción Bw que apunta hacia B, y el lado CG es proporcional a la fuerza de atracción Cw que apunta hacia C;
3– el punto óptimo D está situado en la intersección de las dos circunferencias dibujadas alrededor de los triángulos construidos ABE y BCG.
Se puede dibujar un tercer triángulo de fuerzas ACF, donde F está ubicado fuera del triángulo ABC, basado en el lado AC, y se puede trazar una tercera circunferencia alrededor de ese triángulo. Esa tercera circunferencia cruza a las dos anteriores en el mismo punto D.
Solución geométrica de Tellier del triángulo del problema de atracción-repulsión

Existe una solución geométrica para el problema del triángulo de atracción-repulsión. Su descubrimiento es bastante reciente.[6] Esa solución geométrica difiere de las dos anteriores ya que, en este caso, los dos triángulos de fuerzas construidos se superponen al triángulo de ubicación A1A2R (donde A1 y A2 son puntos de atracción, y R, uno de repulsión), mientras que, en los casos anteriores, nunca lo hicieron.
Esta solución es tal que:
1– en el triángulo construido RA2H, que se superpone parcialmente al triángulo de ubicación A1A2R, el lado RA2 es proporcional a la fuerza de atracción A1w que apunta hacia A1, el lado derecho es proporcional a la fuerza de atracción A2w que apunta hacia A2, y el lado A2H es proporcional a la fuerza repulsiva Rw empujando desde el punto R;
2– en el triángulo construido RA1I, que se superpone parcialmente al triángulo de ubicación A1A2R, el lado RA1 es proporcional a la fuerza de atracción A2w que apunta hacia A2, el lado RI es proporcional a la fuerza de atracción A1w que apunta hacia A1, y el lado A1I es proporcional a la fuerza repulsiva Rw empujando desde el punto R;
3– el punto óptimo D está situado en la intersección de las dos circunferencias dibujadas alrededor de los triángulos construidos RA2H y RA1I.
Esta solución es inútil si una de las fuerzas es mayor que la suma de las otras dos o si los ángulos no son compatibles. En algunos casos, ninguna fuerza es mayor que las otras dos y los ángulos no son compatibles; entonces, la ubicación óptima se encuentra en el punto que ejerce la mayor fuerza de atracción.
Solución trigonométrica de Tellier de los triángulos de los problemas de Fermat y de Weber
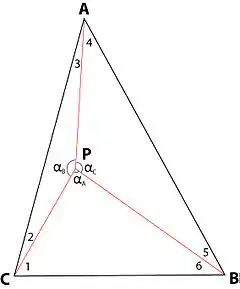
Más de 332 años separan la primera formulación del problema del triángulo de Fermat y el descubrimiento de su solución numérica no iterativa, existiendo una solución geométrica durante casi todo ese período de tiempo. ¿Hay una explicación para esta circunstancia? Esa explicación radica en la posibilidad de que los orígenes de los tres vectores orientados hacia los tres puntos de atracción no coincidan. Si esos orígenes coinciden y se encuentran en la ubicación óptima P, los vectores orientados hacia A, B y C, y los lados del triángulo de ubicación ABC forman los seis ángulos ∠1, ∠2, ∠3, ∠4, ∠5, y ∠6, y los tres vectores forman los ángulos ∠αA, ∠αB y ∠αC. Es fácil escribir las siguientes seis ecuaciones que vinculan seis incógnitas (los ángulos ∠1, ∠2, ∠3, ∠4, ∠5 y ∠6) con seis valores conocidos (ángulos ∠A, ∠B y ∠C, cuyos valores se dan, y los ángulos ∠αA, ∠αB y ∠αC, cuyos valores dependen únicamente de la magnitud relativa de las tres fuerzas de atracción que apuntan hacia los puntos de atracción A, B y C):
- ∠1 + ∠2 = ∠C ;
- ∠3 + ∠4 = ∠A ;
- ∠5 + ∠6 = ∠B ;
- ∠1 + ∠6 + ∠αA = 180° ;
- ∠2 + ∠3 + ∠αB = 180° ;
- ∠4 + ∠5 + ∠αC = 180°.
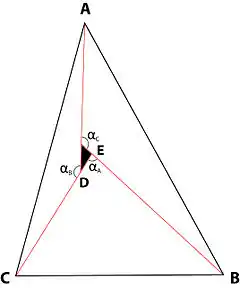
Desafortunadamente, este sistema de seis ecuaciones simultáneas con seis incógnitas es indeterminado, y la posibilidad de que los orígenes de los tres vectores orientados hacia los tres puntos de atracción no coincidan explica por qué. En el caso de no coincidencia, se observa que las seis ecuaciones siguen siendo válidas. Sin embargo, la ubicación óptima de P ha desaparecido debido al agujero triangular que existe dentro del triángulo. De hecho, como ha demostrado Tellier (1972),[2] ese agujero triangular tenía exactamente las mismas proporciones que los “triángulos de fuerzas” dibujados en la solución geométrica de Simpson.
Para resolver el problema, se debe agregar a las seis ecuaciones simultáneas un séptimo requisito, que establece que no debe haber un agujero triangular en el medio del triángulo de ubicación. En otras palabras, los orígenes de los tres vectores deben coincidir.
La solución de Tellier de los problemas del triángulo de Fermat y Weber implica tres pasos:
1– Determinar los ángulos ∠αA, ∠αB y ∠αC que son tales que las tres fuerzas de atracción Aw, Bw y Cw se cancelan entre sí para asegurar el equilibrio. Esto se hace mediante las siguientes ecuaciones independientes:
- cos ∠αA = −( Bw2 + Cw2 − Aw2) / (2 Bw Cw) ;
- cos ∠αB = −( Aw2 + Cw2 − Bw2) / (2 Aw Cw) ;
- cos ∠αC = −( Aw2 + Bw2 − Cw2) / (2 Aw Bw) ;
2– Determinar el valor del ángulo ∠3 (esta ecuación se deriva del requisito de que el punto D debe coincidir con el punto E):
- tan ∠3 = (k sen k’) / (1 + k cos k’) ;
donde k = (CB/CA) (sin ∠αB / sin ∠αA), y k’ = (∠A +∠B + ∠αC) − 180°;
3– Resolver el siguiente sistema de ecuaciones simultáneas donde ahora se conoce ∠3:
- ∠1 + ∠2 = ∠C ;
- ∠3 + ∠4 = ∠A ;
- ∠5 + ∠6 = ∠B ;
- ∠1 + ∠6 + ∠αA = 180° ;
- ∠2 + ∠3 + ∠αB = 180° ;
- ∠4 + ∠5 + ∠αC = 180°.
Solución trigonométrica de Tellier del triángulo del problema de atracción-repulsión

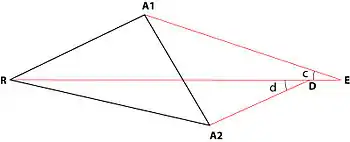
Tellier (1985)[5] extendió el problema de Fermat-Weber al caso de las fuerzas repulsivas. Examínese el caso del triángulo donde hay dos fuerzas atractivas A1w y A2w, y una fuerza repulsiva Rw. Aquí como en el caso anterior, existe la posibilidad de que los orígenes de los tres vectores no coincidan. Entonces la solución debe requerir su coincidencia. La solución trigonométrica de Tellier de este problema es la siguiente:
1– Determinar el ángulo ∠e :
- cos ∠e = -( A1w2 + A2w2 − Rw2) / (2 A1w A2w) ;
2– Determinar el ángulo ∠p :
- cos ∠p = -( A1w2 + Rw2 − A2w2) / (2 A1w Rw) ;
3– Determinar el ángulo ∠c :
- ∠c = 180° − ∠p;
4– Determinar el ángulo ∠d :
- ∠d = ∠e − ∠c;
5– Determinar el valor del ángulo ∠3 (esta ecuación se deriva del requisito de que el punto D debe coincidir con el punto E):
- tan ∠3 = x / y ;
donde x = sin ∠f – (RA1/RA2)(sin ∠d sin [∠e − ∠b] / sin ∠c) ; y y = (RA1/RA2)(sen ∠d cos [∠e − ∠b] / sin ∠c) − cos ∠f ;
6– Determinar ∠1 :
- ∠1 = 180° − ∠e − ∠3;
7– Determinar ∠5 :
- ∠5 = 180° − ∠b − ∠c − ∠1 ;
8– Determinar ∠2 :
- ∠2 = ∠a − ∠5 .
Soluciones iterativas de los problemas de Fermat, Weber y de atracción-repulsión
Cuando el número de fuerzas es superior a tres, ya no es posible determinar los ángulos que separan las diversas fuerzas sin tener en cuenta la geometría del polígono de ubicación. Los métodos geométricos y trigonométricos son entonces insuficientes. En tales casos se utilizan métodos iterativos de optimización. Kuhn y Kuenne (1962)[1] sugirieron un algoritmo basado en mínimos cuadrados reponderados iterativamente generalizando la mediana geométrica para el problema sin pesos. Su método es válido para los problemas de Fermat y Weber que involucran muchas fuerzas, pero no para el problema de atracción-repulsión. En este método, para encontrar una aproximación al punto y minimizando la suma ponderada de distancias
se encuentra una aproximación inicial a la solución y0, y luego en cada etapa del algoritmo se acerca a la solución óptima al establecer yj + 1 como el punto que minimiza la suma de las distancias cuadradas ponderadas
donde los pesos iniciales wi de los puntos de entrada se dividen por las distancias de cada punto a la aproximación de la etapa anterior. Como única solución óptima a un problema de mínimos cuadrados ponderados, cada aproximación sucesiva se puede encontrar como un promedio ponderado:
Para el problema de atracción-repulsión se debe recurrir al algoritmo propuesto por Chen, Hansen, Jaumard y Tuy (1992).[7]
Interpretación de la teoría de la renta de la tierra a la luz del problema de atracción-repulsión
En el campo de la economía espacial, las fuerzas repulsivas son omnipresentes. Los valores de la tierra son la principal ilustración de ello. De hecho, una parte sustancial de la teoría del valor de la tierra, tanto rural como urbana, se puede resumir de la manera que se explica a continuación.
En el caso de que todo el mundo se sienta atraído por un único punto de atracción (el mercado rural o el distrito central de negocios urbano), la competencia entre los distintos postores que quieren ubicarse en el centro generará valores de suelo que transformarán el único punto de atracción de la zona en un punto de repulsión desde el punto de vista del valor del suelo y, en el equilibrio, cada habitante y actividad se ubicará en el punto donde se anularán las fuerzas de atracción y repulsión que ejerce el centro sobre ellos.
El problema de atracción-repulsión y la Nueva Geografía Económica
El problema de Tellier precedió al surgimiento de la Nueva Geografía Económica. Ottaviano y Thisse (2005)[8] lo vieron como un preludio de la Nueva Geografía Económica (NEG) que se desarrolló en la década de 1990, por la que Paul Krugman recibió un Nobel Conmemorativo en Ciencias Económicas en 2008. El concepto de fuerza de atracción es similar al concepto de la Nueva Geografía Económica de aglomeración o fuerza centrípeta, y el concepto de fuerza repulsiva es similar al concepto de dispersión o de fuerza centrífuga.
Referencias
- Kuhn, Harold W. and Robert E. Kuenne, 1962, "An Efficient Algorithm for the Numerical Solution of the Generalized Weber Problem in Spatial Economics." Journal of Regional Science 4, 21–34.
- Tellier, Luc-Normand, 1972, “The Weber Problem: Solution and Interpretation”, Geographical Analysis, vol. 4, no. 3, pp. 215–233.
- Simpson, Thomas, 1750, The Doctrine and Application of Fluxions, London.
- Weber, Alfred, 1909, Über den Standort der Industrien, Tübingen, J.C.B. Mohr) — English translation: The Theory of the Location of Industries, Chicago, Chicago University Press, 1929, 256 pages.
- Tellier, Luc-Normand, 1985, Économie spatiale: rationalité économique de l'espace habité, Chicoutimi, Gaëtan Morin éditeur, 280 pages.
- Tellier, Luc-Normand, 2013, « Annexe 1 : Solution géométrique du cas triangulaire du problème d’attraction-répulsion », annex of the paper of Pierre Hansen, Christophe Meyer and Luc-Normand Tellier, « Modèles topodynamique et de la Nouvelle économie géographique : compatibilité, convergence et avantages comparés », in Marc-Urbain Proulx (ed.), 2013, Sciences du territoire II : méthodologies, Québec, Presses de l’Université du Québec.
- Chen, Pey-Chun, Hansen, Pierre, Jaumard, Brigitte and Hoang Tuy, 1992, "Weber's Problem with Attraction and Repulsion," Journal of Regional Science 32, 467–486.
- Ottaviano, Gianmarco and Jacques-François Thisse, 2005, « New Economic Geography: what about the N? », Environment and Planning A 37, 1707–1725.
Bibliografía
- Chen, Pey-Chun, Hansen, Pierre, Jaumard, Brigitte and Hoang Tuy, 1992, "Weber's Problem with Attraction and Repulsion," Journal of Regional Science 32, 467–486.
- Kuhn, Harold W. and Robert E. Kuenne, 1962, "An Efficient Algorithm for the Numerical Solution of the Generalized Weber Problem in Spatial Economics." Journal of Regional Science 4, 21–34.
- Ottaviano, Gianmarco and Jacques-François Thisse, 2005, « New Economic Geography: what about the N? », Environment and Planning A 37, 1707–1725.
- Simpson, Thomas, 1750, The Doctrine and Application of Fluxions, London.
- Tellier, Luc-Normand and Boris Polanski, 1989, “The Weber Problem: Frequency of Different Solution Types and Extension to Repulsive Forces and Dynamic Processes”, Journal of Regional Science, vol 29, no. 3, p. 387–405.
- Tellier, Luc-Normand, 1972, “The Weber Problem: Solution and Interpretation”, Geographical Analysis, vol. 4, no. 3, pp. 215–233.
- Tellier, Luc-Normand, 1985, Économie spatiale: rationalité économique de l'espace habité, Chicoutimi, Gaëtan Morin éditeur, 280 pages.
- Tellier, Luc-Normand, 2013, « Annexe 1: Solution géométrique du cas triangulaire du problème d’attraction–répulsion », annex of the paper of Pierre Hansen, Christophe Meyer and Luc-Normand Tellier, « Modèles topodynamique et de la Nouvelle économie géographique : compatibilité, convergence et avantages comparés », in Marc-Urbain Proulx (ed.), 2013, Sciences du territoire II : méthodologies, Québec, Presses de l’Université du Québec.
- Weber, Alfred, 1909, Über den Standort der Industrien, Tübingen, J.C.B. Mohr) — English translation: The Theory of the Location of Industries, Chicago, Chicago University Press, 1929, 256 pages.
- Wesolowski, Georges, 1993, «The Weber problem: History and perspective», Location Science, Vol. 1, p. 5–23.
Enlaces externos
- Hazewinkel, Michiel, ed. (2001), «Weber problem», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
 Portal:Matemáticas. Contenido relacionado con Matemáticas.
Portal:Matemáticas. Contenido relacionado con Matemáticas.