Programación genética

En 1954, GP se inició con los algoritmos evolutivos utilizado por primera vez por Nils Aall Barricelli y aplicados a simulaciones evolutivas. En 1960 y principios de 1970, los algoritmos evolutivos fueron reconocidos como métodos de optimización. Ingo Rechenberg y su grupo fueron capaces de resolver problemas complejos de ingeniería a través de estrategias de evolutivas como lo documenta en su tesis PhD en 1971 y el libro resultante de 1973. John Holland fue muy influyente durante la década de 1970.

En 1964, Lawrence J. Fogel, uno de los primeros profesionales de la metodología de GP, aplica los algoritmos evolutivos para el problema de descubrir autómatas de estado finito. Más tarde, el trabajo relacionado con GP surgió la comunidad de los sistemas de clasificación basado en aprendizaje, la cual desarrolló un conjunto de reglas que describen las políticas óptimas para los procesos de decisión de Markov. La primera declaración de la moderna GP "basado en árboles" (es decir, procedimiento con una estructuración basada en árboles y operadores adecuadamente definidos en GA) fue dada por Nichael L. Cramer (1985).[1] Este trabajo fue posteriormente ampliado en gran medida por John R. Koza., un proponente principal de GP que ha sido pionero en la aplicación de GP en la optimización de diversos y complejos problemas de búsqueda.[2] Gianna Giavelli, un estudiante de Koza, luego fue el pionero en el uso de GP como una técnica para modelar la expresión del ADN.[3]

En la década de los 1990's, GP se utilizó principalmente para resolver problemas relativamente simples, ya que es muy costoso computacionalmente. Recientemente, GP ha producido novedosos y excelentes resultados en áreas como la computación cuántica, diseño electrónico, juegos, ordenamiento y búsqueda, debido a las mejoras en la tecnología GP y la crecimiento exponencial de la potencia de la CPU.[4] Estos resultados incluyen la reproducción o el desarrollo de varias invenciones posteriores al año 2000. GP también se ha aplicado a los programas de computadoras, así como hardware evolutivo.

El desarrollo de una teoría de la GP ha sido muy difícil, por lo que en la década de 1990's GP fue considerado una especie de paria entre las técnicas de búsqueda.

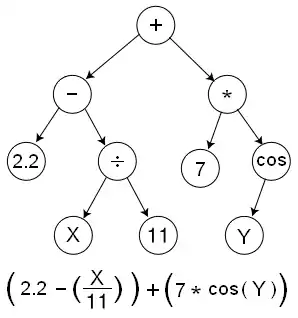
GP desarrolla programas informáticos, tradicionalmente representados en la memoria como estructuras de árboles.[5] Los árboles pueden ser fácilmente evaluados de forma recursiva. Cada nodo del árbol tiene una función como operador y cada nodo terminal tiene un operando, por lo que las expresiones matemáticas son fáciles de evolucionar y evaluar. Así, tradicionalmente GP favorece el uso de lenguaje de programación que, naturalmente, introduce las estructuras de árbol (por ejemplo, Lisp; otros lenguajes de programación funcionales también son adecuados).

Representaciones que no utilizan árboles se han sugerido y aplicado con éxito, tales como programación genética lineal, la cual se adapta a los tradicionales lenguajes imperativos [véase, por ejemplo, Banzhaf et al. (1998)]. El software comercial de GP Discipulus utilizan la inducción automática de código máquina binario ("AIM")[6] para lograr un mejor rendimiento. μGP[7] usa multigrafos dirigidos para generar programas que explotan al máximo la sintaxis de un dado lenguaje ensamblador.

Los principales operadores usados en algoritmos evolutivos así como GP son cruzamiento y mutación.

Las ideas básicas de la programación genética han sido modificadas y extendidas en una variedad de formas:

• Extended Compact Genetic Programming (ECGP)
• Embedded Cartesian Genetic Programming (ECGP)
• Probabilistic Incremental Program Evolution (PIPE)

La Programación Meta-Genética es la técnica de evolucionar meta de aprendizaje un sistema de programación usando su propia programación genética. Se sugiere que los cromosomas, el cruzamiento, y la mutación vayan evolucionando ellos mismos, por lo tanto, al igual que sus homólogos en la vida real deben ser flexibles al cambio en el medio escogido por un programador humano. Programación Meta-Genética fue propuesta formalmente por Jürgen Schmidhuber en 1987.[8] Doug Lenat Eurisko es un esfuerzo anterior que puede ser la misma técnica. Se trata de un algoritmo recursivo pero de terminación, lo que le permite evitar una recursión infinita.

Los críticos de esta idea a menudo dicen este enfoque es demasiado amplio en su alcance. Sin embargo, podría ser posible restringir el criterio de la aptitud en una clase general de los resultados, y así obtener un GP evolucionado que sería más eficiente para producir resultados para las sub-clases. Esto podría tomar la forma de una Meta evolutiva GP para producir algoritmos humanos caminantes que se utilizan para evolucionar el funcionamiento humano como correr, saltar, etc. El criterio de aptitud aplicado a la Meta-GP simplemente sería el de eficiencia.

Para las clases de problemas generales puede no haber manera de demostrar que Meta-GP pueda ser viable producir resultados de manera más eficiente que un algoritmo creado mediante distintos enfoques. Lo mismo vale para GP estándar y otros algoritmos de búsqueda.

• Sistemas bioinspirados
• Programación de expresiones de genes
• Evolución gramatical

• Banzhaf, W., Nordin, P., Keller, R.E., and Francone, F.D. (1998), Genetic Programming: An Introduction: On the Automatic Evolution of Computer Programs and Its Applications, Morgan Kaufmann
• Barricelli, Nils Aall (1954), Esempi numerici di processi di evoluzione, Methodos, pp. 45–68.
• Brameier, M. and Banzhaf, W. (2007), Linear Genetic Programming, Springer, New York
• Carmona, Enrique; Fernández, Severino (2020). Fundamentos de la Computación Evolutiva. Marcombo. ISBN 978-8426727558.
• Cramer, Nichael Lynn (1985), "A representation for the Adaptive Generation of Simple Sequential Programs" in Proceedings of an International Conference on Genetic Algorithms and the Applications, Grefenstette, John J. (ed.), Carnegie Mellon University
• Crosby, Jack L. (1973), Computer Simulation in Genetics, John Wiley & Sons, London.
• Fogel, David B. (2000) Evolutionary Computation: Towards a New Philosophy of Machine Intelligence IEEE Press, New York.
• Fogel, David B. (editor) (1998) Evolutionary Computation: The Fossil Record, IEEE Press, New York.
• Forsyth, Richard (1981), BEAGLE A Darwinian Approach to Pattern Recognition Kybernetes, Vol. 10, pp. 159–166.
• Fraser, Alex S. (1957), Simulation of Genetic Systems by Automatic Digital Computers. I. Introduction. Australian Journal of Biological Sciences vol. 10 484-491.
• Fraser, Alex and Donald Burnell (1970), Computer Models in Genetics, McGraw-Hill, New York.
• Holland, John H (1975), Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor
• Korns, Michael (2007), Large-Scale, Time-Constrained, Symbolic Regression-Classification, in Genetic Programming Theory and Practice V. Springer, New York.
• Korns, Michael (2009), Symbolic Regression of Conditional Target Expressions, in Genetic Programming Theory and Practice VII. Springer, New York.
• Korns, Michael (2010), Abstract Expression Grammar Symbolic Regression, in Genetic Programming Theory and Practice VIII. Springer, New York.
• Koza, J.R. (1990), Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to Solve Problems, Stanford University Computer Science Department technical report STAN-CS-90-1314. A thorough report, possibly used as a draft to his 1992 book.
• Koza, J.R. (1992), Genetic Programming: On the Programming of Computers by Means of Natural Selection, MIT Press
• Koza, J.R. (1994), Genetic Programming II: Automatic Discovery of Reusable Programs, MIT Press
• Koza, J.R., Bennett, F.H., Andre, D., and Keane, M.A. (1999), Genetic Programming III: Darwinian Invention and Problem Solving, Morgan Kaufmann
• Koza, J.R., Keane, M.A., Streeter, M.J., Mydlowec, W., Yu, J., Lanza, G. (2003), Genetic Programming IV: Routine Human-Competitive Machine Intelligence, Kluwer Academic Publishers
• Langdon, W. B., Genetic Programming and Data Structures, Springer ISBN 0-7923-8135-1
• Langdon, W. B., Poli, R. (2002), Foundations of Genetic Programming, Springer-Verlag ISBN 3-540-42451-2
• Nordin, J.P., (1997) Evolutionary Program Induction of Binary Machine Code and its Application. Krehl Verlag, Muenster, Germany.
• Poli, R., Langdon, W. B., McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely available from the internet. ISBN 978-1-4092-0073-4.
• Rechenberg, I. (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
• Schmidhuber, J. (1987). Evolutionary principles in self-referential learning. (On learning how to learn: The meta-meta-... hook.) Diploma thesis, Institut f. Informatik, Tech. Univ. Munich.
• Smith, S.F. (1980), A Learning System Based on Genetic Adaptive Algorithms, PhD dissertation (University of Pittsburgh)
• Smith, Jeff S. (2002), Evolving a Better Solution, Developers Network Journal, March 2002 issue
• Shu-Heng Chen et al. (2008), Genetic Programming: An Emerging Engineering Tool, International Journal of Knowledge-based Intelligent Engineering System, 12(1): 1-2, 2008.
• Weise, T, Global Optimization Algorithms: Theory and Application, 2008.

• Riccardo Poli, William B. Langdon, Nicholas F. McPhee, John R. Koza, "A Field Guide to Genetic Programming" (2008)
• DigitalBiology.NET Vertical search engine for GA/GP resources
• Aymen S Saket & Mark C Sinclair
• The Hitch-Hiker's Guide to Evolutionary Computation
• GP bibliography
• People who work on GP