Punto de Exeter

En geometría, el punto de Exeter es un punto especial asociado con cualquier triángulo. Es uno de los puntos característicos o "centros" de un triángulo, designado como centro X(22) en la Enciclopedia Clark Kimberling de Puntos Notables del Triángulo.[1] Fue descubierto en un taller de matemáticas por ordenador en la Academia Phillips Exeter en 1986[2] (la ciudad de Exeter, sede de la academia , pertenece al estado de New Hampshire).

Es uno de los puntos notables de un triángulo definidos más recientemente, a diferencia de los puntos clásicos como el centroide, el incentro, o el punto de Steiner, conocidos en algunos casos desde la más remota antigüedad.[3]

Definición

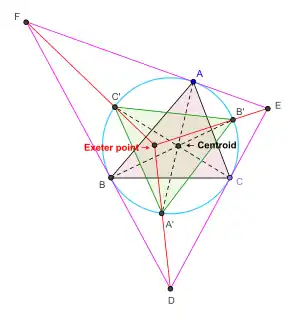
El punto de Exeter se define como sigue:[2][4]

Sea ABC un triángulo cualquiera dado. Trácense las medianas a través de los vértices A, B y C; conocida la circunferencia circunscrita del triángulo ABC, se obtienen sus intersecciones A', B' y C' con las medianas. Se construye el triángulo DEF, formado por las tangentes en A, B, y C a la circunferencia anterior (siendo D el vértice opuesto al lado formado por la tangente en el vértice A; E el vértice opuesto al lado formado por la tangente en el vértice B; y F el vértice opuesto al lado formado por la tangente en el vértice C). Las líneas a través de DA', EB' y FC' son concurrentes, y su punto de intersección es el punto de Exeter del triángulo ABC.

Coordenadas trilineales

Las coordenadas trilineales del punto de Exeter son:

( a ( b4 + c4 - a4 ), b ( c4 + a4 - b4 ), c ( a4 + b4 - c4 ) )

Propiedades

Referencias
  1. Kimberling, Clark. «Encyclopedia of Triangle Centers: X(22)». Consultado el 24 de mayo de 2012.
  2. Kimberling, Clark. «Exeter Point». Consultado el 24 de mayo de 2012.
  3. Kimberling, Clark. «Triangle centers». Consultado el 24 de mayo de 2012.
  4. Weisstein, Eric W. «Exeter Point». From MathWorld--A Wolfram Web Resource. Consultado el 24 de mayo de 2012.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.