Radio de Einstein
El radio de Einstein es el radio de un anillo de Einstein, y es un ángulo característico de las lentes gravitacionales en general, ya que las distancias típicas entre imágenes en las lentes gravitacionales son del orden del radio de Einstein.[1]
Cálculo
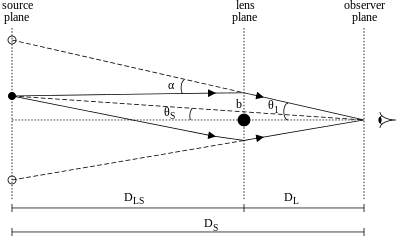
Para el cálculo del radio de Einstein, asumiremos que toda la masa M de la galaxia con lente L se concentra en el centro de la galaxia.
Para una masa puntual, la deflexión se puede calcular y es una de las clásicas pruebas de la relatividad general. Para ángulos pequeños α1, la deflexión total por una masa puntual M viene dada (ver métrica de Schwarzschild) por
dónde
- b1 es el parámetro de impacto (la distancia de aproximación más cercana del rayo de luz al centro de masa)
- G es la constante gravitacional,
- cc es la velocidad de la luz.
Al observar que, para ángulos pequeños y con el ángulo expresado en radianes, el punto de aproximación más cercano b1 en un ángulo θ1 para la lente L en una distancia DL está dado por b1 = θ1 DL, podemos volver a expresar el ángulo de flexión α1 como
- ..... (Ecuación 1)
Si establecemos θS como el ángulo en el que se vería la fuente sin la lente (que generalmente no es observable), y θ1 como el ángulo observado de la imagen de la fuente con respecto a la lente, entonces se puede ver desde la geometría de lente (contando distancias en el plano de la fuente) que la distancia vertical abarcada por el ángulo θ1 a una distancia DS es la misma que la suma de las dos distancias verticales θS DS y α1 DLS. Esto da la ecuación de la lente
que se puede reorganizar para dar
- ..... (Ec. 2)
Al establecer (ec. 1) igual a (ec. 2) y reorganizar, obtenemos
Para una fuente justo detrás de la lente, θS = 0, la ecuación de la lente para una masa puntual da un valor característico para θ1 que se llama ángulo de Einstein, denotado θE. Cuando θE se expresa en radianes, y la fuente de lente está lo suficientemente lejos, el radio de Einstein, denotado RE, viene dado por
- . [2]
Poniendo θS = 0 y despejando θ1 da
El ángulo de Einstein para una masa puntual proporciona una escala lineal conveniente para hacer variables de lente adimensionales. En términos del ángulo de Einstein, la ecuación de la lente para una masa puntual se convierte en
La sustitución de las constantes da
En la última forma, la masa se expresa en masas solares (M☉) y las distancias en Gigaparsec (Gpc). El radio de Einstein es más prominente para una lente típicamente a medio camino entre la fuente y el observador.
Para un cúmulo denso con masa Mc ≈ 10 × 1015 M☉ a una distancia de 1 Gigaparsec (1 Gpc), este radio podría ser tan grande como 100 segundos de arco (llamado macrolente). Para una búsqueda de evento de microlente gravitacional (con masas de orden 1 M☉) a distancias galácticas (digamos D ~ 3 kpc), el radio de Einstein típico sería del orden de milisegundos de arco. En consecuencia, es imposible observar imágenes separadas en eventos de microlente con las técnicas actuales.
Asimismo, para el rayo de luz inferior que llega al observador desde debajo de la lente, tenemos
y
y por lo tanto
El argumento anterior se puede ampliar para lentes que tienen una masa distribuida, en lugar de una masa puntual, utilizando una expresión diferente para el ángulo de curvatura α, las posiciones θI(θS) de las imágenes se pueden calcular. Para pequeñas deflexiones, este mapeo es uno a uno y consiste en distorsiones de las posiciones observadas que son invertibles. A esto se le llama lente débil. Para grandes deflexiones, se pueden tener varias imágenes y un mapeo no invertible: esto se llama lente fuerte. Tenga en cuenta que para que una masa distribuida dé como resultado un anillo de Einstein, debe ser axialmente simétrica.
Referencias
- Drakeford, Jason; Corum, Jonathan; Overbye, Dennis (5 de marzo de 2015). «Einstein’s Telescope - video (02:32)». The New York Times. Consultado el 27 de diciembre de 2015.
- https://ned.ipac.caltech.edu/level5/March04/Kochanek2/Kochanek3.html
Bibliografía
- Chwolson, O (1924). «Über eine mögliche Form fiktiver Doppelsterne». Astronomische Nachrichten 221 (20): 329-330. Bibcode:1924AN....221..329C. doi:10.1002/asna.19242212003.
- Einstein, Albert (1936). «Lens-like Action of a Star by the Deviation of Light in the Gravitational Field». Science 84 (2188): 506-507. Bibcode:1936Sci....84..506E. JSTOR 1663250. PMID 17769014. doi:10.1126/science.84.2188.506. Archivado desde el original el 29 de abril de 2018. (The famous Einstein Ring paper)
- Renn, Jurgen; Tilman Sauer; John Stachel (1997). «The Origin of Gravitational Lensing: A Postscript to Einstein's 1936 Science paper». Science 275 (5297): 184-186. Bibcode:1997Sci...275..184R. PMID 8985006. doi:10.1126/science.275.5297.184.