Reflector de esquina

Un reflector de esquina es un catadióptrico que consta de tres planos, perpendiculares dos a dos, que refleja los rayos directamente hacia la fuente, pero desplazados. A menudo las tres superficies que se cortan tienen formas cuadradas. Los que se utilizan para reflejar las ondas de radar suelen estar fabricados en metal. Los reflectores ópticos, que se utilizan en agrimensura y para telémetros láser, utilizan prismas triangulares de vidrio.

Un reflector de esquina para pruebas de radar

El término también se utiliza para una antena de reflector de esquina, que consta de dos superficies metálicas planas en ángulo recto, con una antena dipolo delante de ellos.

Principio físico
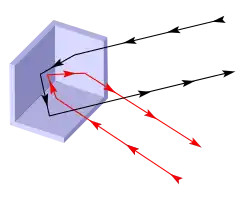
Principio físico de un reflector de esquina
Animación que muestra los rayos reflejados en una esquina de un cubo (principio del reflector de esquina)

Un rayo incidente se refleja tres veces, una vez por cada superficie, lo que conlleva la inversión del sentido de su dirección.[1][2] Para visualizarlo, se debe tener en cuenta que los tres vectores normales correspondientes a los lados perpendiculares de la esquina se puede considerar que forman una base (un sistema de coordenadas rectangulares) (x, y, z) en el que la dirección de un rayo entrante arbitraria se representa por [a, b, c]. Cuando el rayo se refleja en el primer lado, por ejemplo x , la componente del rayo en x, (el valor a), se invierte y pasa a ser -a, mientras que las componentes y, y z, no se modifican, resultando una dirección [-a, b, c]. De manera similar, cuando el rayo se refleja en el lado y, y finalmente en el lado z , las componentes b y c se invierten. Así, la dirección del rayo pasa de ser [a, b, c ] a convertirse en [-a, b, c]; luego pasa a [-a, -b , c]; y finalmente se transforma en [-a, -b, -c], de forma que tras incidir en el reflector de esquina, el rayo sale exactamente con sus tres componentes en el sentido inverso.

En radar

Los reflectores de radar de esquina están diseñados para reflejar las ondas de radio, las microondas emitidas por un radar de nuevo hacia la antena del radar, sirviendo de fuente de "retorno" en las pantallas de radar para calibrar el dispositivo. Un reflector de esquina simple consta de tres chapas metálicas o superficies de pantalla formando ángulos de 90° entre sí, unidas una a otra en los bordes, formando una "esquina". Reflejan hacia atrás y paralelamente las ondas de radio incidentes. Para crear un reflector de esquina en el que se reflejen las ondas de radar procedentes de cualquier dirección, se colocan 8 reflectores de esquina en forma de un octaedro (coloquialmente, en forma de diamante). Para poder funcionar correctamente, las superficies reflectantes deberán ser mayores que varias longitudes de onda de las señales a reflejar.[3]

Un reflector radar de esquina (objeto en forma de diamante) en el mástil de un yate (Nota: El reflector no está colocado correctamente; para reflejar mejor el radar de superficie, debe desplegarse en la llamada configuración de "captura de lluvia")
Reflectores de esquina utilizados en radar
Una boya en la Bahía de San Diego con placas en ángulo en la parte superior
Reflector de radar en un pilar de un puente
Un multirreflector en el sitio de pruebas de Nevada utilizado como objetivo de radar para un bombardeo nuclear simulado


En navegación marítima se colocan en los pilares de los puentes, boyas, barcos (especialmente en los de madera) y, sobre todo, en los botes salvavidas, para garantizar que aparezcan con nitidez en las pantallas de radar de los barcos. Los reflectores de esquina se colocan en los mástiles del buque a una altura de al menos 4,6 metros sobre el nivel del mar. Como los radares marinos utilizan la banda X de microondas, con longitudes de onda de entre 2,5 y 3,75 cm, se suelen emplear reflectores pequeños, de menos de 30 cm de diámetro. En navegación aérea, los reflectores de esquina se instalan en las pistas de zonas rurales, para hacer que aparezcan en el radar de las aeronaves.

En óptica
Esquina de cubo reflectora
Retrorreflector de alcance láser lunar (LRRR) del Apolo 15 instalado en la Luna

En óptica, normalmente, los reflectores de esquina constan de tres espejos reflectantes o caras de un prisma que devuelven el haz de luz incidente en la dirección opuesta. En topografía, los prismas retrorreflectores se utilizan comúnmente como objetivos para realizar la medición electrónica de distancias con una estación total.

Un reflector triangular de esquina como corte de un cubo

Matrices de pequeños reflectores de esquina se utilizan en automóviles y bicicletas en las luces traseras. Microscópicas estructuras reflectoras de esquina se pueden incorporar en la pintura reflectante para aumentar la visibilidad durante la noche, aunque son más comunes para este propósito glóbulos esféricos retrorreflectores.

Una antena direccional utilizando la intersección de dos superficies planas conductoras también se considera un tipo de reflector de esquina.

Otros ejemplos

Se pueden crear reflectores de esquina accidentalmente. Los bloques de pisos con balcones a menudo son reflectores de esquina casuales para el sonido y devolver un eco peculiar para un observador haciendo un ruido agudo, como un aplauso, en las proximidades. De manera similar, en la interpretación de radar, un objeto que tiene múltiples reflexiones de las superficies lisas produce un retorno de radar de mayor magnitud del que podría esperarse a partir del tamaño físico del objeto. Este efecto se empezó a utilizar en el ADM-20 Quail, un pequeño misil que tenía la misma sección transversal radar que un B-52.

La NASA ha situado varios reflectores angulares ópticos de cuarzo en la Luna, en el conocido como el experimento de medición láser lunar. Mediante la medida del tiempo que una luz láser tarda en llegar a la Luna y volver se puede determinar la distancia a la órbita lunar de forma muy precisa.

Véase también

Referencias
  1. Newman, William I. (2019). Continuum Mechanics in the Earth Sciences. Cambridge University Press. pp. 6-7. ISBN 978-0-521-56289-8.
  2. Bernstein, Matt A.; Friedman, William A. (2011). Thinking About Equations: A Practical Guide for Developing Mathematical Intuition in the Physical Sciences and Engineering. Wiley. p. 193. ISBN 978-1-118-21064-2.
  3. Kraus, John; Marhefka, Ronald (2002). Antennas for All Applications (3rd edición). McGraw Hill. p. 365. ISBN 0-07-112240-0.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.