Sistema diédrico

El sistema diédrico es un método de representación geométrica de los elementos del espacio tridimensional sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyección ortogonal sobre dos planos que se cortan perpendicularmente. El sistema formado por los dos planos se denomina diedro. Para generar las vistas diédricas, uno de los planos se abate sobre el segundo, permitiendo la representación de las proyecciones de los elementos en un plano (papel).

Representación en sistema diédrico de un volumen con forma de letra «L»: Las dos figuras de la izquierda son las proyecciones o vistas principales de la pieza. La figura de la derecha es la vista lateral de la misma pieza, o su proyección lateral.

Es un método gráfico de representación que consiste en obtener la imagen de un objeto (en planta y alzado), mediante la vista proyección de haces perpendiculares a dos planos principales de proyección, horizontal (PH) y proyección vertical (PV). El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.

Si se prescinde de la línea de tierra, se denomina sistema diédrico directo.

Introducción
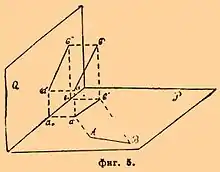
Firma para indicar el uso del sistema europeo de proyección

La geometría descriptiva es la rama de las matemáticas que estudia la representación de cuerpos tridimensionales sobre superficies bidimensionales, empleando para ello los principios y procedimientos de la geometría métrica y proyectiva, y usando como medio de expresión al Dibujo Técnico. Los teoremas propuestos por la Geometría Descriptiva apuntan a lograr una relación unívoca entre cada uno de los elementos geométricos que componen al objeto representado y su correspondiente representación bidimensional, así como a la verificación de la reversibilidad de la representación, esto es, que así como a partir de un objeto en el espacio es siempre posible obtener sus proyecciones sobre una superficie bidimensional, de igual manera, a partir    de las proyecciones de dicho objeto, es factible determinar la posición espacial de cualquiera de los puntos que componen a tal objeto. El sistema básico dentro de esta geometría es el sistema diédrico o de proyecciones diédricas ortogonales. Gaspard Monge, geómetra francés, fue quien codificó su estudio y mecanismo; para ello nos valemos de dos planos proyectantes que forman entre sí un ángulo recto (de 90°).

Planos proyectantes principales

Los dos planos proyectantes principales son el Horizontal y el Vertical. Su intersección se denomina Línea de tierra.

  • Plano Horizontal (PH): contiene la proyección horizontal o planta. Está subdividido por la Línea de tierra (LT) en: Plano horizontal Posterior (detrás) y Plano Horizontal Anterior (delante).
  • Plano Vertical (PV): contiene la proyección vertical o alzado. Está subdividido por la Línea de Tierra en: Plano Vertical Superior (arriba) y Plano Vertical Inferior (abajo).
Las tres proyecciones ortogonales principales: frontal, superior y lateral (alzado, planta y perfil).

Normalmente, solo se usan los planos PH y PV, que se cortan en la Línea de tierra (LT) dando origen a una subdivisión del espacio en cuatro ángulos diedros o cuadrantes.

Para representar en dos dimensiones (sobre un papel) las vistas principales en el sistema diédrico, se realiza un abatimiento, que consiste en girar, tumbar, o abatir un plano principal de tal manera que el Plano Horizontal (PH) se superponga al Plano Vertical (PV).

También se utiliza, como plano auxiliar, el denominado:

  • Plano de Perfil (PP): contiene la proyección lateral izquierda (o derecha).
Planos bisectores

Los dos planos bisectores son aquellos que dividen a los cuadrantes en dos octantes de 45° cada uno. El primer bisector está en el primero y tercer cuadrante y el segundo bisector en el segundo y cuarto cuadrante. Los planos bisectores se definen como el lugar geométrico de puntos con idéntica cota y alejamiento.

Representación de un punto

Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo de sombras) sobre los planos principales: proyección horizontal y proyección vertical.

Cota

Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT). Es decir, su distancia en el eje Z.

Alejamiento

Se denomina alejamiento de un punto del espacio a la distancia entre él y su proyección en el plano vertical, que equivale a la distancia entre la proyección horizontal y la línea de Tierra (LT). Es decir, su distancia en el eje Y.

Las proyecciones vertical y horizontal de un punto siempre se encuentran alineadas, siendo el segmento que los une perpendicular a la línea de Tierra (LT).

Lateralidad

Se denomina lateralidad o distancia al origen de un punto del espacio a su situación (derecha o izquierda) respecto a la línea de tierra (LT). Es decir, su distancia en el eje X.

Determinación por coordenadas

Un punto puede determinarse por coordenadas. El origen de este sistema será la intersección de los planos principales: horizontal, vertical y de perfil.

  • El eje X está determinado por la recta intersección de los planos horizontal y vertical, es decir, sobre la Línea de tierra.
  • El eje Y está determinado por la recta intersección de los planos horizontal y de perfil.
  • El eje Z está determinado por la recta intersección de los planos vertical y de perfil.

Representación de una recta


Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella. Conociendo las parejas de proyecciones de dos puntos de una recta, se obtiene la proyección uniéndolos.

Trazas de una recta

Las trazas de una recta son los puntos de intersección con los planos principales (PV y PH).

Representación de un plano

Un plano está definido mediante sus dos trazas: la vertical y la horizontal. Las trazas de un plano son las rectas de intersección con los planos principales (PV y PH).

Una recta pertenece a un plano, si la traza vertical de la recta es un punto de la traza vertical del plano y, además, la traza horizontal de la recta es un punto de la traza horizontal del plano.

Abatimientos

Para obtener, en verdadera magnitud, la representación de una figura contenida en un plano cualquiera, se abate dicho plano sobre uno de los principales.

Representación de un volumen geométrico

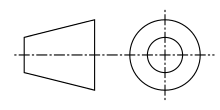
Un cuerpo geométrico se representa mediante la proyección de sus aristas, sus generatrices extremas, o su contorno (esfera). Las aristas o generatrices más próximas al punto de vista se representan como segmentos de trazo continuo, y las posteriores, u ocultas, mediante segmentos de trazo discontinuo. Las zonas seccionadas se indican mediante trazos paralelos inclinados.

Representación de una circunferencia

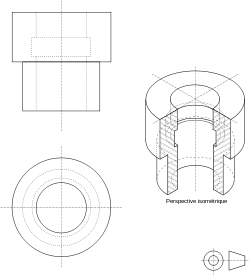
La proyección de una circunferencia es, generalmente, una elipse. Será otra circunferencia semejante si está contenida en un plano paralelo a uno principal. Puede ser un segmento si está de perfil respecto de un plano principal, siendo su longitud la del diámetro.

Diferentes sistemas

Según como estén reflejadas las proyecciones en el plano del dibujo, existen dos sistemas de representación:

  • Sistema europeo: Las proyecciones se recogen tras el objeto. Son vistas en el primer cuadrante.
  • Sistema americano: Las proyecciones se reflejan desde el objeto. Son vistas en el tercer cuadrante.

Aunque en ambos sistemas las proyecciones (representaciones del objeto) son exactamente las mismas, su disposición en el plano del dibujo es la inversa.

Véase también
Proyección gráfica
Proyección paralela
 

Proyección ortogonal

 
 

Proyección oblicua

 
 
 

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.