Slope Mass Rating
El Slope Mass Rating o SMR es una clasificación geomecánica desarrollada por el profesor Dr. Manuel Romana Ruíz en el año 1985 para caracterizar taludes excavados en roca.[1][2][3] El sistema hace uso de la ampliamente utilizada clasificación geomecánica Rock Mass Rating (RMR).[4]
Definición
Las clasificaciones geomecánicas consideran una serie de parámetros que condicionan la resistencia y deformabilidad del macizo rocoso (p. ej. las orientaciones de las discontinuidades, la densidad de fractura, la resistencia de la roca intacta), y permiten cuantificar la calidad geomecánica de un afloramiento rocoso. El SMR es una adaptación del RMR de Bieniawski para su aplicación a taludes rocosos ampliamente utilizada.[5][6] Las puntuaciones del SMR varían entre 0 y 100, siendo 100 la puntuación correspondiente a un macizo rocoso de una elevada calidad geomecánica. El término macizo rocoso comprende la roca intacta que lo constituye y las discontinuidades que lo afectan.
Cálculo del índice SMR
El SMR utiliza los mismos cinco factores de puntuación que el RMR:
- La resistencia a compresión simple de la roca intacta,
- El Rock Quality Designation (o RQD),
- El espaciado de las discontinuidades,
- El estado de las discontinuidades (que consta de la suma de cinco sub-parámetros), y
- Las condiciones hidráulicas de las discontinuidades.
El sexto parámetro consiste en un ajuste por la orientación de la discnotinuidad, el cual es especialmente importante para evaluar la estabilidad de taludes rocosos. El SMR proporciona recomendaciones cuantitativas para evaluar este índice de corrección a través de cuatro parámetros, tres dependientes de las relaciones geométricas entre la discontinuidad y el talud y una cuarta qué dependiente del método de excavación empleado. El SMR fue originalmente definido para considerar roturas planas y por vuelco. Sin embargo, Anbalagan et al. adaptaron la clasificación original para roturas por cuña[7]
El SMR se calcula mediante la expresión:
Dónde:
- RMRb es el índice RMR básico resultante de aplicar la clasificación de Bieniawski.
- F1 depende del paralelismo (A) entre las direcciones de las discontinuidades y del talud. Varía entre 0.15 y 1.0. Adopta el valor de 0.15 cuando el ángulo entre el plano de la discontinuidad y el talud es mayor de 30° y, por tanto, la probabilidad de rotura es muy pequeña. Sin embargo, cuando ambos planos son paralelos o subparalelos, alcanza el valor de 1.0.
- F2 se refiere al buzamiento de la discontinuidad B, siendo βj en roturas planas. Su valor varía entre 0.15 a 1.0. Vale 0.15 cuando el buzamiento de la junta es menor que 20° y 1.0 para buzamientos mayores de 45°. Para la rotura por vuelco, F2 toma el valor de 1.0.
- F3 se refiere a la relación entre los buzamientos del talud y de las discontinuidades. Adopta los valores originales propuestos por Bieniawski, que son siempre negativos.
- F4 es un factor de corrección que depende del método de excavación empleado para la ejecución del talud.
SMR continuo
Tomás et al.[10] propusieron funciones continuas alternativas para el cálculo de los parámetros de corrección F1, F2 y F3. Estas funciones proporcionan diferencias absolutas máximas con las funciones discretas inferiores a 7 puntos, permitiendo reducir significativamente las interpretaciones subjetivas durante su cálculo. Además, las funciones para el cálculo de los factores de ajuste del SMR reduce las incertidumbres sobre qué puntuación asignar a valores situados cerca de los límites de los intervalos definidos en la clasificación original discreta.
La función propuesta para el cálculo de F1 es:
Dónde el parámetro A es el ángulo formado entre las direcciones de la discontinuidad y del talud para roturas planares y vuelcos y el ángulo formado entre la intersección de las dos discontinuidades y la dirección de buzamiento del plano para roturas por cuña. Es importante tener en cuenta que la operación "Arctangent" está expresada en grados.
Dónde parámetro B es el buzamiento de la discontinuidad, en grados, para roturas planas y el plunge de la línea de intersección para roturas por cuña. Es importante tener en cuenta que el operador "arctangent" se expresa en grados.
Dónde C depende de la relación de buzamientos de la discontinuidad y del talud (para vuelcos o roturas planas) y el buzamiento del talud y la inmersión de línea de la inmersión para roturas por cuña. La operación "Arctangent" está expresadas en grados.
SMR gráfico
Alternativamente, Tomás et al.[11] propusieron un método gráfico basado en el uso de la proyección estereográfica de las discontinuidades y del talud para obtener los parámetros de corrección del SMR (F1, F2 y F3). Este método permite determinar los factores de corrección de forma rápida y sencilla para un talud, así como en diversas aplicaciones prácticas como taludes de infraestructuras lineales, minería o trincheras.
Otras modificaciones
El SMR ha sido también adaptado a diferentes situaciones y aplicaciones a través de diversas modificaciones. Por ejemplo la clasificación ha sido adaptada a taludes de gran altura, formaciones flysch o incluso a taludes constituidos por materiales heterogéneos.[12][13]
Análisis de sensibilidad del SMR
Tomás et al[14] desarrollaron un análisis de sensibilidad visual 4-D del SMR usando la metodología Worlds within Worlds para explorar, analizar y visualizar las relaciones entre los principales parámetros de esta clasificación geomecánica. El análisis reveló la existencia de varios casos en los que las relaciones geométricas talud-discontinuidad no presentaban apenas influencia en la estabilidad del talud (i.e. F1×F2×F3≃0), y por tanto, el SMR puede ser calculado corrigiendo el RMR básico únicamente con el factor F4 cometiendo un error máximo de 9 puntos usando la siguiente expresión:
Estos casos en los que la influencia de la geometría del talud y de la discontinuidad es despreciable (i.e. F1×F2×F3≃0) son:
a) Para rotura plana
- βs < βj;
- A mayor que 30° y βj < 20°
b) Para rotura por cuña
- βs < βi;
- A mayor que 30° y βi; < 20 °C) Para rotura por vuelco
- βj < 30°
- A mayor que 30°
- βj+βs ≤ 120°
Donde βs es el ángulo del talud, βj es el buzamiento de la discontinuidad, βi es la inmersión de la línea de intersección entre las dos discontinuidades de la cuña y A es el paralelismo entre la discontinuidad (o la línea de intersección las dos discontinuidades para el caso de rotura por la cuña) y la dirección de buzamiento del talud.
Herramientas para el cálculo del SMR
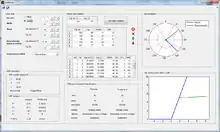
El SMR puede ser empleado a través de la aplicación de código abierto SMRTool,[15] la cual permite calcular el SMR a partir de datos geomecánicos del macizo rocoso y la orientación de las discontinuidades y del talud. Este programa se ha usado de forma exitosa para calcular el SMR usando nubes de puntos 3D.[16]
Aplicaciones del SMR mediante Sistemas de Información Geográfica
Algunos autores han propuesto diversas metodologías para crear mapas de susceptibilidad a la rotura de taludes rocosos mediante el empleo del SMR usando Sistemas de Información Geográfica (SIG).[17][18][19]
Véase también
Referencias
- Romana M. (1985). New adjustment ratings for application of Bieniawski classification to slopes. Proc. Int. Symp. on the Role of Rock Mechanics: 49-53.
- Romana M. (1995). The geomechanical classification SMR for slope correction. Proc. Int. Congress on Rock Mechanics 3: 1085-1092.
- STMR. «STMR Servicio Tecnico de Mecanica de Rocas». www.stmr.es. Consultado el 31 de marzo de 2016.
- Bieniawski, Z.T. (1989). Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering. John Wiley & Sons. ISBN 978-0-471-60172-2.
- R. Tomás; M. Romana; J.B. Serón (2016). Revisión del estado actual de la clasificación geomecánica Slope Mass Rating (SMR) (2016). Revisión del estado actual de la clasificación geomecánica Slope Mass Rating (SMR). 10° Simposio Nacional Ingeniería Geotécnica. La Coruña, 19-21 Octubre de 2016
- «Slope Mass Rating (SMR) geomechanics classification: thirty years review». Romana, M., Tomás, R., Serón, J.B. (2015). Slope Mass Rating (SMR) geomechanics classification: thirty years review (2015). The 13th ISRM Congress. Quebec, Canada,10-13 de May, 2015. ISBN: 978-1-926872-25-4. Consultado el 25 de agosto de 2018.
- Evaluación de estabilidad de masa de rock que utiliza modificado SMR aproximación.
- Romana M. El papel de las clasificaciones geomecánicas en el estudio de la estabilidad de taludes. In: del IV Simposio Nacional sobre taludes y laderas inestables, vol. 3; 1997:955–1011.
- Anbalagan R, Sharma S, Raghuvanshi TK. Rock mass stability evaluation using modified SMR approach. In: Proceedings of 6th nat symp rock mech, Bangalore, India, 1992. p. 258–68
- Tomás, R.; Delgado, J.; Serón, J.B. (2007-10). «Modification of slope mass rating (SMR) by continuous functions». International Journal of Rock Mechanics and Mining Sciences 44 (7): 1062-1069. ISSN 1365-1609. doi:10.1016/j.ijrmms.2007.02.004. Consultado el 25 de agosto de 2018.
- «A graphical approach for slope mass rating (SMR)». Engineering Geology (en inglés) 124: 67-76. 4 de enero de 2012. ISSN 0013-7952. doi:10.1016/j.enggeo.2011.10.004. Consultado el 25 de agosto de 2018.
- Romana, M., Serón, J.B., Montalar, E., SMR Geomechanics classification: Application, experience and validation ISRM 2003–Technology roadmap for rock mechanics, South African Institute of Mining and Metallurgy, 2003.
- Romana, M., Tomás, R., Serón, J.B. (2015). Slope Mass Rating (SMR) geomechanics classification: thirty years review. ISRM Congress 2015 Proceedings - International Symposium on Rock Mechanics, Quebec, Canada, May 10 to 13 2015. ISBN 978-1-926872-25-4, 10 pp
- Tomás, R.; Valdes-Abellan, J.; Tenza-Abril, A. J.; Cano, M. (1 de julio de 2012). «New insight into the slope mass rating geomechanical classification through four-dimensional visualization». International Journal of Rock Mechanics and Mining Sciences 53: 64-69. doi:10.1016/j.ijrmms.2012.04.002.
- Adrián, Riquelme Guill,; Roberto, Tomás Jover,; Antonio, Abellán Fernández,. «SMRTool (MATLAB)». rua.ua.es. Consultado el 8 de abril de 2016.
- Riquelme, Adrián J.; Tomás, Roberto; Abellán, Antonio (1 de abril de 2016). «Characterization of rock slopes through slope mass rating using 3D point clouds». International Journal of Rock Mechanics and Mining Sciences 84: 165-176. doi:10.1016/j.ijrmms.2015.12.008.
- Irigaray, C., Fernández, T. & Chacón, J. Preliminary Rock-Slope-Susceptibility Assessment Using GIS and the SMR Classification. Natural Hazards, 30, 309-324, doi: 10.1023/B:NHAZ.0000007178.44617.c6.
- Tomás, R., Cano, M., Cañaveras, J.C:, Cuenca, A., Delgado, J., Estévez, A., Pina, J.A., Nuevas funciones continuas para el cálculo del Slope Mass Rating (SMR): aplicación mediante un sistema de información geográfica a los taludes rocosos de una cantera. Revista de la Sociedad Geológica de España, 19, 87-97, 2006
- Yilmaz, I., Marschalko, M., Yildirim, M., Dereli, E. & Bednarik, M. 2012. GIS-based kinematic slope instability and slope mass rating (SMR) maps: application to a railway route in Sivas (Turkey). Bulletin of Engineering Geology and the Environment, 71, 351-357, doi: 10.1007/s10064-011-0384-5.
