Submuestreo
En el procesamiento de señal digital, submuestreo, compresión y diezmado son términos asociados con el proceso de remuestreo en un sistema de procesamiento de señal digital de velocidad múltiple. Tanto el submuestreo como el diezmado pueden ser sinónimos de compresión, o pueden describir un proceso completo de reducción del ancho de banda (filtrado) y reducción de la frecuencia de muestreo.[1][2] Cuando el proceso se realiza en una secuencia de muestras de una señal u otra función continua, produce una aproximación de la secuencia que se habría obtenido al muestrear la señal a una velocidad menor (o densidad, como en el caso de una fotografía).
Diezmado es un término que históricamente significa la extracción de cada décima parte.[3] Pero en procesamiento de señal, significa mantener solo la décima muestra. Este factor multiplica el intervalo de muestreo o, de manera equivalente, divide la frecuencia de muestreo. Por ejemplo, si el audio de un disco compacto, procesado a razón de 44 100 muestras/segundo, es diezmado en un factor de 5/4, la frecuencia de muestreo resultante es de 35 280. Un componente del sistema que realiza el diezmado se denomina diezmador. El diezmado por un factor entero también se llama compresión.[4][5]
Submuestreo por un factor entero
La reducción de la tasa de muestreo por un factor entero M puede ser explicada como proceso de dos pasos, con una implementación equivalente que es más eficaz:[3]
- Reduce los componentes de señal de alta frecuencia con un filtro paso bajo digital.
- Diezmar la señal filtrada por M; esto es, mantener solamente cada M-ésima muestra.
El paso 2 solo permite que los componentes de señal de alta frecuencia sean malinterpretados por los usuarios posteriores de los datos, lo cual es una forma de distorsión llamada aliasing. El paso 1, cuando es necesario, suprime los alias a un nivel aceptable. En esta aplicación, el filtro se denomina filtro antialiasing o antisolapamiento y su diseño se describe seguidamente.
Cuándo el filtro antialiasing es un diseño IIR , se basa en la retroalimentación de salida a entrada, antes del segundo paso. Con el filtrado FIR, es fácil calcular solo cada M-ésima salida. El cálculo realizado por un filtro FIR de diezmado para la n-ésima muestra de salida es un producto de puntos, descrito por la ecuación:[4]
Dónde la matriz es la respuesta al impulso y es su longitud. representa la secuencia de entrada que está siendo submuestreada. En un procesador de señales de propósito general, después de calcular , la manera más fácil de hallar es avanzar el índice de inicio en la matriz x [] por M y volver a calcular el producto de puntos. En el caso de M=2, puede diseñarse como filtro de media banda, donde casi la mitad de los coeficientes son cero y no es necesario incluirlos en los productos de punto.
Los coeficientes de respuesta al impulso tomados a intervalos de M forman una subsecuencia, y hay M subsecuencias (fases) multiplexadas juntas. El producto de puntos es la suma de los productos de puntos de cada subsecuencia con las muestras correspondientes de la secuencia x []. Además, debido al submuestreo en un factor de M, el flujo de muestras x[] involucradas en cualquiera de los M productos de puntos nunca está involucrado en los otros productos de punto. Por lo tanto, los filtros FIR de bajo orden M están filtrando cada una de las M fases multiplexadas del flujo de entrada, y las M salidas se están sumando. Este punto de vista ofrece una implementación diferente que podría ser ventajosa en una arquitectura multiprocesador. En otras palabras, el flujo de entrada se demultiplexa y se envía a través de un banco de M filtros cuyas salidas se suman. Cuando se implementa de esa manera, se llama filtro polifásico.
Para completar, ahora mencionamos que una implementación posible, pero poco probable, de cada fase es reemplazar los coeficientes de las otras fases con ceros en una copia de la matriz h [], procesar la secuencia original x [] a la velocidad de entrada ( lo que significa mucha multiplicación por ceros), y diezmar la salida por un factor de M. La equivalencia de este método ineficiente y la implementación descrita anteriormente se conoce como la primera identidad Noble.[6][3]
Filtro Anti-aliasing
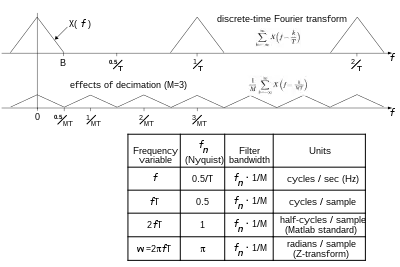
Sea X (f) la transformada de Fourier de cualquier función, x (t), cuyas muestras en algún intervalo, T, sean iguales a la secuencia x[n]. Entonces, la transformada de Fourier de tiempo discreto (DTFT) es una representación en serie de Fourier de una suma periódica de X (f):[1]
Cuándo T tiene unidades de segundos, es expresado en hercios (Hz). Reemplazando T con MT en las fórmulas anteriores da el DTFT de la secuencia diezmada, x[nM], según la ecuación:
La sumatoria periódica ha sido reducida en amplitud y periodicidad por un factor de M. Un ejemplo de estas distribuciones está descrito en los dos curvas de al Figura 1.[Más bajo-alfa 5][más bajo-alfa 6] El aliasing o solapamiento ocurre cuándo copias adyacentes de X(f) se solapan. El propósito del filtro anti-aliasing el filtro es el de asegurar que la periodicidad reducida no genere solapamientos o alias. La condición que asegura que las copias de X(f) no se solapen unas a otras es que el ancho de banda cumpla la desigualdad:
ya que esta es la máxima frecuencia de corte de un filtro antialiasing ideal.
Submuestreo en un factor racional
Sea M/L el factor de diezmado, donde: M, L ∈ ℤ; M > L. Los pasos 1 y 2 ahora son los siguientes:
- Aumentar (remuestrear) la secuencia por un factor de L. A esto se le llama muestreo ascendente o interpolación.
- Diezmar en un factor de M.
El paso 1 requiere un filtro paso bajo después de incrementar la tasa de datos, y el paso 2 requiere otro antes del diezmado. Por tanto, ambas operaciones pueden ser cumplidas por un solo filtro con la más baja de las dos frecuencias de corte. Para el caso en que M > L, la frecuencia más baja de corte es ciclos por muestra intermedia.
Referencias
- Oppenheim, Alan; Schafer, Ronald; Buck, John (1999). Discrete-time signal processing (en inglés) (2 edición). Prentice Hall. pp. 143, 168. ISBN 0-13-754920-2. Consultado el 27 de junio de 2020. (requiere registro).
- Tan, Li (21 de abril de 2008). «Multirate DSP, part 1: Upsampling and downsampling» (en inglés). AspenCore, Inc. Consultado el 27 de junio de 2020.
- Harris, Frederic J. (24 de mayo de 2004). Multirate signal processing for communication systems (en inglés). Prentice-Hall. pp. 20-21, 25, 128. ISBN 0131465112.
- Crochiere, Ronald E.; Rabiner, Lawrence R. (1983). Multirate digital signal processing (en inglés) (2 edición). Prentice-Hall. p. 32. ISBN 0136051626.
- Poularikas, Alexander (Septiembe de 1998). The handbook of formulas and tables for signal processing (en inglés) (1 edición). CRC Press. pp. 42-48. ISBN 0849385792.
- Strang, Gilbert; Nguyen, Truong (1996). Wavelets and Filter Banks (en inglés) (2 edición). Wellesley-Cambridge Press. pp. 100-101. ISBN 0961408871.
Enlaces externos
- Esta obra contiene una traducción derivada de «Downsampling (signal processing)» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.