Superficie de Morin
La superficie de Morin es el modelo a medio camino de la eversión de la esfera, descubierta por el matemático francés Bernard Morin. Cuenta con simetría de rotación cuádruple.
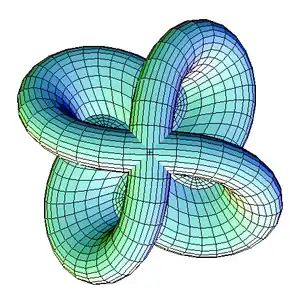
Caracterización
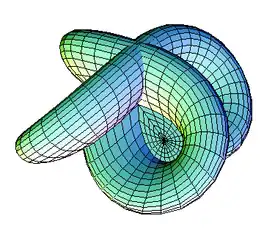


Si la esfera original que se va a evertir tiene su superficie exterior de color verde y su superficie interior de color rojo, entonces cuando la esfera se transforme a través de homotopía en una superficie de Morin, la mitad visible hacia el exterior será verde y la otra mitad roja:
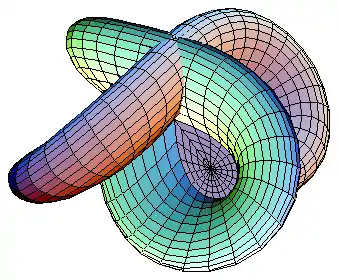
La mitad de una superficie de Morin corresponde al exterior (verde) de la esfera
a la que es homeomorfa, y la otra mitad simétrica al interior (rojo).
Luego, al girar la superficie 90° alrededor de su eje de simetría, se intercambiarán sus colores, es decir, se intercambiará la polaridad interior-exterior de la superficie orientable, de modo que volver sobre los pasos de la homotopía exactamente en la misma posición hasta la esfera original después de haber rotada de esta manera la superficie de Morin producirá una esfera cuya superficie exterior es roja y cuya superficie interior es verde: una esfera que se ha vuelto del revés. El siguiente es un resumen de la eversión:
1. Esfera: verde por fuera, roja por dentro...
2. se transforma en una...
3. superficie de Morin.
3'. La superficie de Morin girada 90°...
2'. se transforma inversamente en...
1'. una esfera: roja por fuera, verde por dentro.
Estructura de la superficie de Morin
La superficie de Morin se puede separar en cuatro cuartos de sección congruentes. Estas secciones pueden llamarse aquí sección Este, sección Sur, sección Oeste y sección Norte, o — respectivamente — sección 0, sección 1, sección 2 y sección 3.
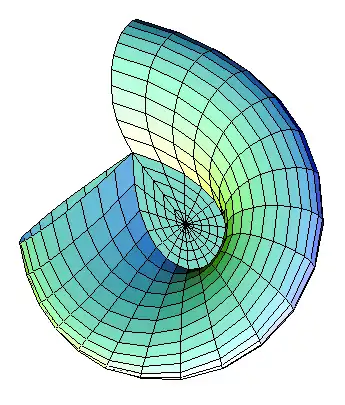
- Sección Este de la superficie de Morin.
La superficie de Morin tiene un punto cuádruple por donde pasa su eje de simetría. Este punto cuádruple es el punto de partida y el punto final de seis líneas de puntos dobles. Cada una de las secciones de un cuarto está delimitada por tres de estas líneas de puntos dobles, de modo que cada sección de un cuarto es homeomorfa a un triángulo. La sección Este se muestra aquí esquemáticamente:
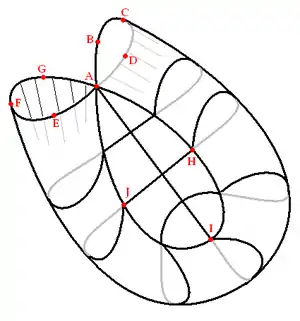
El diagrama muestra la sección Este delimitada por tres bucles: ABCDA, AEFGA y AHIJA. El tercer bucle, AHIJA, es una línea de puntos dobles donde la sección Este se cruza consigo misma. El bucle ABCDA es solo una línea de puntos dobles cuando la sección Este se une a la sección Oeste, y el bucle AEFGA es solo una línea de puntos dobles cuando la sección Este se une a la sección Sur. El punto es el punto cuádruple que en realidad es la superposición de cuatro puntos diferentes: A0, A1, A2, A3.
Así es como la sección Este se une a las otras secciones: cada uno de sus bucles delimitadores se especifica por un quíntuple ordenado de puntos, y entonces
donde los puntos sin prima pertenecen a la sección 0 (Este), los puntos con prima pertenecen a la sección 1 (Sur), los puntos con prima doble pertenecen a la sección 2 (Oeste) y los puntos con prima triple pertenecen a la sección 3 (Norte).
Los tres bucles restantes conectan secciones de la siguiente manera:
La sección Este tiene, considerada en sí misma, un bucle de puntos dobles: AHIJA. Si se desenrolla y aplana la superficie el resultado será el siguiente:
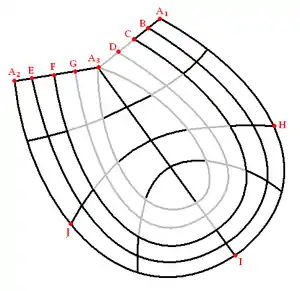
que es homeomorfo a un triángulo:
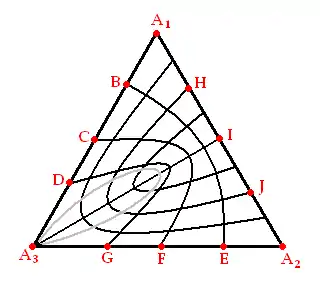
Unir las cuatro secciones triangulares en sus costuras producirá un tetraedro:
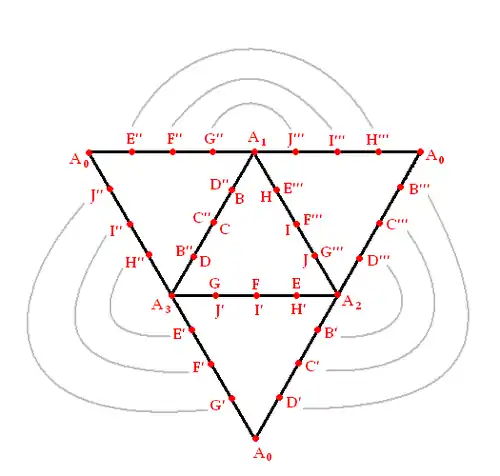
que es homeomorfo a una esfera, lo que demuestra que la superficie de Morin es una esfera que se interseca a sí misma.
Galería de la superficie Morin
.PNG.webp)
- Cuatro vistas diferentes de la superficie de Morin: las dos primeras se muestran con "barreras de paso" recortadas, las dos últimas son vistas desde la "parte inferior".
Superficie analítica de Morin
La superficie de Morin se puede describir elegantemente mediante un conjunto de ecuaciones[1] en versión abierta (con polos enviados al infinito) o cerrada.
Galería de superficie Morin analítica
|
Modelo reglado de la superficie abierta de Morin 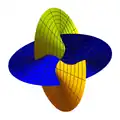 Vista superior 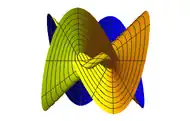 Vista diagonal 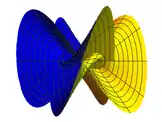 Vista lateral |
Superficie de Morin cerrada  Vista superior  Vista diagonal 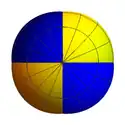 Vista lateral |

Véase también
Referencias
- Bednorz, Adam; Bednorz, Witold (2017). «Analytic sphere eversion with minimum of topological events». .