Teoría de grafos extremales
La teoría de grafos extremales es una rama de las matemáticas que estudia cómo es que propiedades globales de un grafo pueden influir en su subestructura local.[1] Esta rama abarca un vasto número de resultados que describen cómo ciertas propiedades de las gráficas - número de vértices, número de aristas, densidad de aristas, número cromático, o cintura, por ejemplo - garantizan la existencia de ciertas subestructuras locales.
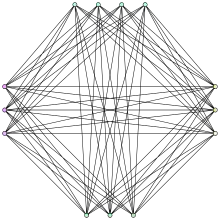
Uno de los principales objetos de estudio de esta área de teoría de grafos son los grafos extremales, que son o bien maximales o minimales con respecto a algún parámetro global, y tales que contienen (o no contienen) cierta subestructura local - ya sea un clique, o una coloración de sus aristas.
Ejemplos
La teoría de grafos extremales puede ser motivada por preguntas tales como las siguientes:
Pregunta 1. ¿Cuál es el máximo número posible de aristas en un grafo con vértices tal que no contiene un ciclo?
Si un grafo con vértices contiene al menos aristas, entonces debe contener un ciclo. Más aún, cualquier árbol en vértices contiene aristas y no contiene ciclos. Por lo tanto, la respuesta a esta pregunta es , y los árboles son los grafos extremales.[2]
Pregunta 2. Si un grafo con vértices no contiene ningún triángulo como subgrafo, ¿cuál es el máximo número de aristas que puede tener?
Por el Teorema de Mantel, la respuesta a esta pregunta es . El grafo extremal correspondiente es el grafo bipartito completo en vértices; es decir, tal que sus dos partes difieren en tamaño en a lo más 1.
La siguiente es una generalización de la Pregunta 2:
Pregunta 3. Sea un entero positivo. ¿Cuántas aristas debe haber en un grafo con vértices para garantizar que, sin importar cómo las aristas estén distribuidas, el clique esté embedido como subgrafo?
La respuesta a esta pregunta es
,
y proviene del Teorema de Turán. Por lo tanto, si un grafo con vértices es -libre, entonces puede tener a lo sumo este número de aristas:
.
El grafo extremal correspondiente es un Grafo de Turán, el cual se puede contemplar en la Figura de arriba. Es la unión completa de grafos independientes, con distribución de tamaños lo más equitativa posible.
A continuación, una generalización de la Pregunta 3 para grafos no-completos:
Pregunta 4. Sea un entero positivo, y un grafo no completo. ¿Cuántas aristas debe haber en un grafo con vértices para garantizar que, sin importar cómo las aristas estén distribuidas, el clique esté embedido como subgrafo?
La respuesta a esta pregunta proviene del Teorema de Erdös-Stone.
Varios de los resultados fundamentales de la teoría extremal de grafos provienen de respuestas a preguntas formuladas de la manera siguiente:
Pregunta 5. Dada una propiedad , una invariante , y una familia de grafos , queremos encontrar el mínimo valor posible de cierto parámetro global del grafo tal que cualquier grafo en con cumple la propiedad .
En la Pregunta 1, por ejemplo, corresponde al conjunto de grafos en -vértices, a la propiedad de contener un ciclo, al parámetro que cuenta la cantidad de aristas, y .
Historia
La teoría de grafos extremales es, en su sentido más estricto, una rama de la teoría de grafos desarrollada y amada por los Húngaros. |
El Teorema de Mantel (1907), así como el Teorema de Turán (1941) fueron de los primeros grandes descubrimientos en la teoría extremal de grafos.[3] En particular, el Teorema de Turán pronto se convertiría en una motivación para probar resultados tales como el Teorema de Ërdos-Stone-Simonovits (1946).[4] Este último resultado es interesante, ya que relaciona el número cromático con el máximo número de aristas en un grafo que es -libree. Una demostración alternativa de Ërdos-Stone-Simonovits fue encontrada 1975, y utilizaba el Teorema de Szemerédi, una técnica esencial para la resolución de problemas de teoría de grafos extremal.[3]
Algunos resultados: densidades y desigualdades
Un parámetro global cuyo rol es central en la teoría de grafos extremal es la densidad de homomorfismos. Dado un grafo y otro grafo , su densidad de homomorfismo de
.
En particular, edge density is the subgraph density for , for a graph , its subgraph density is defined as
.
Los teoremas mencionados en secciones previas de este artículo pueden ser reformulados en términos de densidades de homomorfismos. Por ejemplo, el Teorema de Mantel implica que la densidad de homomorfismo de en un grafo libre de triángulos es a lo sumo . El Teorema de Turán implica que si un grafo es -libre, entonces .
Más aún, el Teorema de Ërdos-Stone-Simonovits establece que
donde es el máximo número de aristas posible que un grafo -libre con vértices puede tener, y es el número cromático de . Una interpretación de este resultado es que la densidad de homomorfismo con respecto a (arista) en un grafo -libre graph es asintóticamente .
Otro resultado por Ërdos, Reyni y Sós (1966) establece que un grafo en que no contiene copias de como subgrafo, tiene a lo sumo la siguiente cantidad de aristas.
Condiciones relacionadas al grado mínimo
Los teoremas de la sección previa prueban la existencia de un objeto pequeño en un grafo que es posiblemente muy grande. Hay, sin embargo, otro tipo de teoremas en teoría extremal de grafos, que consisten en buscar condiciones que garanticen la existencia de una estructura que cubra todos los vértices del grafo. Note que es incluso posible para un grafo denso con vértices y
aristas tener un vértice aislado, aún si casi todas las aristas posibles están presentes en el grafo. Intuitivamente, condiciones tales como el número de ejes no dan indicación suficiente acerca de cómo están distribuidas las aristas en un grafo, lo cual conlleva a resultados que solo garantizan estructuras de tamaño limitado en grafos con una cantidad arbitraria de vértices.
Es, por lo tanto, más útil en algunas ocasiones considerar el parámetro del grado mínimo, definido así
Un grado mínimo que es suficientemente grande descarta la posibilidad de tener vértices 'patológicos'; si el mínimo grado en un grafo fuera 1, por ejemplo, entonces dicho grafo no puede tener vértices aislados, aún si tuviera muy pocas aristas.
Un resultado importante en teoría de grafos extremal es el Teorema de Dirac, que establece que en cualquier grafo con vértices y grado mínimo mayor o igual que contiene un ciclo Hamiltoniano.
Otro teorema[3] establece que si el grado mínimo en un grafo es , y la cintura es , entonces el número de vértices en el grafo es al menos:
Algunas preguntas abiertas
Incluso si muchas observaciones importantes se han podido hacer en el campo de teoría extremal de grafos, muchas preguntas también yacen sin contestar aún. Por ejemplo, el Problema de Zarankiewicz pregunta por el máximo número posible de aristas en un grafo bipartito con vértices que no tiene subgrafos que son completos bipartitos de tamaño .
Otra conjetura importante en teoría extremal de grafos fue formulada por Sidorenko en 1993. Se conjetura que si es un grafo bipartito, entonces su densidad de grafón (una noción generalizada de densidad de homomorfismo) es al menos .
Véase también
- Teoría de Ramsey
- Densidad de homomorfismos
- Problema del subgrafo prohibido
Referencias
- Bollobás, 2004, p. 9
- Bollobás, 2004, p. 9
- Bollobás, 1998, p. 104
- Diestel, 2010
Bibliografía
- Bollobás, Béla (2004), Extremal Graph Theory, New York: Dover Publications, ISBN 978-0-486-43596-1..
- Bollobás, Béla (1998), Modern Graph Theory, Berlin, New York: Springer-Verlag, pp. 103-144, ISBN 978-0-387-98491-9..
- Diestel, Reinhard (2010), Graph Theory (4th edición), Berlin, New York: Springer-Verlag, pp. 169-198, ISBN 978-3-642-14278-9, archivado desde el original el 28 de mayo de 2017, consultado el 7 de enero de 2014..
- M. Simonovits, Slides from the Chorin summer school lectures, 2006.