Teorema de Bayes
El teorema de Bayes, en la teoría de la probabilidad, es una proposición planteada por el matemático inglés Thomas Bayes (1702-1761)[1] y publicada póstumamente en 1763,[2] que expresa la probabilidad condicional de un evento aleatorio dado en términos de la distribución de probabilidad condicional del evento dado y la distribución de probabilidad marginal de solo .
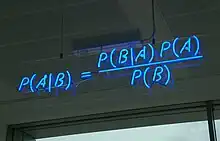
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de dado con la probabilidad de dado . Es decir, por ejemplo, que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza. Muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.
Una de las muchas aplicaciones del teorema de Bayes es la inferencia bayesiana, un enfoque particular de la inferencia estadística. Cuando se aplican, las probabilidades implicadas en el teorema pueden tener diferentes interpretaciones de probabilidad. Con la interpretación probabilidad bayesiana, el teorema expresa cómo un grado de creencia, expresado como una probabilidad, debería cambiar racionalmente para tener en cuenta la disponibilidad de pruebas relacionadas. La inferencia bayesiana es fundamental para la estadística bayesiana, siendo considerada por una autoridad como; "a la teoría de la probabilidad lo que el teorema de Pitágoras es a la geometría."[3]
Historia
El teorema de Bayes debe su nombre al reverendo Thomas Bayes ( /beɪz/), también estadístico y filósofo. Bayes utilizó la probabilidad condicional para proporcionar un algoritmo (su Proposición 9) que utiliza la evidencia para calcular los límites de un parámetro desconocido. Su trabajo se publicó en 1763 con el título Un ensayo para resolver un problema de la doctrina de las probabilidades. Bayes estudió cómo calcular una distribución para el parámetro de probabilidad de una distribución binomial (en terminología moderna). A la muerte de Bayes, su familia transfirió sus documentos a un amigo, el ministro, filósofo y matemático Richard Price.
Durante dos años, Richard Price editó significativamente el manuscrito inédito, antes de enviárselo a un amigo que lo leyó en voz alta en la Royal Society el 23 de diciembre de 1763.[4] Price editó[5] La obra principal de Bayes "An Essay towards solving a Problem in the Doctrine of Chances" (1763), que apareció en Philosophical Transactions,[6] y contiene el teorema de Bayes. Price escribió una introducción al documento que proporciona algunas de las bases filosóficas de la estadística bayesiana y eligió una de las dos soluciones ofrecidas por Bayes. En 1765, Price fue elegido miembro de la Royal Society en reconocimiento a su trabajo sobre el legado de Bayes.[7][8] El 27 de abril se leyó en la Royal Society, y posteriormente se publicó, una carta enviada a su amigo Benjamin Franklin en la que Price aplica este trabajo a la población y al cálculo de las "pensiones vitalicias".[9]
Independientemente de Bayes, Pierre-Simon Laplace en 1774, y más tarde en su Théorie analytique des probabilités de 1812, utilizó la probabilidad condicional para formular la relación de una probabilidad posterior actualizada a partir de una probabilidad previa, dada una evidencia. Reprodujo y amplió los resultados de Bayes en 1774, aparentemente sin conocer el trabajo de Bayes. Laplace refinó el teorema de Bayes a lo largo de varias décadas:
- Laplace anunció su descubrimiento independiente del teorema de Bayes en: Laplace (1774) "Mémoire sur la probabilité des causes par les événements", "Mémoires de l'Académie royale des Sciences de MI (Savants étrangers)", 4: 621-656. Reimpreso en: Laplace, "Oeuvres complètes" (París, Francia: Gauthier-Villars et fils, 1841), vol. 8, pp. 27-65. Disponible en línea en: Gallica. El teorema de Bayes aparece en la p. 29.
- Laplace presentó un refinamiento del teorema de Bayes en: Laplace (leído: 1783 / publicado: 1785) "Mémoire sur les approximations des formules qui sont fonctions de très grands nombres", "Mémoires de l'Académie royale des Sciences de Paris", 423-467. Reimpreso en: Laplace, "Oeuvres complètes" (París, Francia: Gauthier-Villars et fils, 1844), vol. 10, pp. 295-338. Disponible en línea en: Gallica. El teorema de Bayes figura en la página 301.
- Véase también: Laplace, "Essai philosophique sur les probabilités" (París, Francia: Mme. Ve. Courcier [Madame veuve (es decir, viuda) Courcier], 1814), página 10. Traducción inglesa: Pierre Simon, Marqués de Laplace con F. W. Truscott y F. L. Emory, trans, "A Philosophical Essay on Probabilities" (Nueva York, Nueva York: John Wiley & Sons, 1902), página 15.}}[10] La interpretación bayesiana de la probabilidad fue desarrollada principalmente por Laplace.[11]
Unos 200 años más tarde, Sir Harold Jeffreys puso el algoritmo de Bayes y la formulación de Laplace sobre una base axiomático, escribiendo en un libro de 1973 que el teorema de Bayes "es a la teoría de la probabilidad lo que el teorema de Pitágoras es a la geometría".[12]
Stephen Stigler utilizó un argumento bayesiano para concluir que el teorema de Bayes fue descubierto por Nicholas Saunderson, un matemático inglés ciego, algún tiempo antes que Bayes;[13][14] esa interpretación, sin embargo, ha sido discutida.[15] Martyn Hooper[16] y Sharon McGrayne[17] han argumentado que la contribución de Richard Price fue sustancial:
En términos modernos, deberíamos referirnos a la regla de Bayes-Price. Price descubrió el trabajo de Bayes, reconoció su importancia, lo corrigió, contribuyó al artículo y le encontró un uso. La convención moderna de emplear sólo el nombre de Bayes es injusta, pero está tan arraigada que cualquier otra cosa tiene poco sentido.[17]<
Teorema
Sea un conjunto de sucesos mutuamente excluyentes y exhaustivos tales que la probabilidad de cada uno de ellos es distinta de cero . Si es un suceso cualquiera del que se conocen las probabilidades condicionales entonces la probabilidad viene dada por la expresión:
donde:
- son las probabilidades a priori,
- es la probabilidad de en la hipótesis ,
- son las probabilidades a posteriori.
Fórmula de Bayes

Con base en la definición de probabilidad condicionada se obtiene la Fórmula de Bayes, también conocida como Regla de Bayes:
Esta fórmula nos permite calcular la probabilidad condicional de cualquiera de los eventos dado . La fórmula «ha originado muchas especulaciones filosóficas y controversias».[18]
Aplicaciones
El teorema de Bayes es válido en todas las aplicaciones de la teoría de la probabilidad. Sin embargo, hay una controversia sobre el tipo de probabilidades que emplea. En esencia, los seguidores de la estadística tradicional solo admiten probabilidades basadas en experimentos repetibles y que tengan una confirmación empírica mientras que los llamados estadísticos bayesianos permiten probabilidades subjetivas. El teorema puede servir entonces para indicar cómo debemos modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. La estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y el hecho de permitir revisar esas estimaciones en función de la evidencia empírica es lo que está abriendo nuevas formas de hacer conocimiento. Una aplicación de esto son los clasificadores bayesianos que son frecuentemente usados en implementaciones de filtros de correo basura o spam, que se adaptan con el uso. Otra aplicación se encuentra en la fusión de datos, combinando información expresada en términos de densidad de probabilidad proveniente de distintos sensores.
Como observación, se obtiene la siguiente fórmula y su demostración resulta trivial.
Como aplicaciones puntuales:
- El diagnóstico de cáncer.
- Evaluación de probabilidades durante el desarrollo de un juego de bridge por Dan F. Waugh y Frederick V. Waugh.
- Probabilidades a priori y a posteriori.
- Un uso controvertido en la Ley de sucesión de Laplace.[18]
- En el testeo de hipótesis en Ciencia Política cuando se usa metodología process tracing.
Uso en genética
En genética, el teorema de Bayes puede utilizarse para calcular la probabilidad de que un individuo tenga un genotipo específico. Muchas personas buscan aproximar sus posibilidades de estar afectadas por una enfermedad genética o su probabilidad de ser portadoras de un gen recesivo de interés. Se puede realizar un análisis bayesiano basado en los antecedentes familiares o en las pruebas genéticas, con el fin de predecir si un individuo desarrollará una enfermedad o la transmitirá a sus hijos. Las pruebas y la predicción genéticas son una práctica habitual entre las parejas que planean tener hijos pero que están preocupadas por la posibilidad de que ambos sean portadores de una enfermedad, especialmente en comunidades con baja varianza genética.[19]
El primer paso del análisis bayesiano para la genética es proponer hipótesis mutuamente excluyentes: para un alelo específico, un individuo es o no es portador. A continuación, se calculan cuatro probabilidades: Probabilidad Previa (la probabilidad de cada hipótesis teniendo en cuenta información como los antecedentes familiares o las predicciones basadas en la Herencia Mendeliana), Probabilidad Condicional (de un determinado resultado), Probabilidad Conjunta (producto de las dos primeras) y Probabilidad Posterior (un producto ponderado que se calcula dividiendo la Probabilidad Conjunta de cada hipótesis por la suma de ambas probabilidades conjuntas).
Véase también
Enlaces externos
- Calculadora en internet
- Inferencia estadística según el modelo bayesiano, en la web de la Sociedad Andaluza de Enfermedades Infecciosas
- Enciclopedia Stanford de filosofía
- Simulación del Teorema de Bayes con R-Project
- Teorema de Bayes y Probabilidad Condicional A Posteriori
- What Is Bayes’ Theorem & How Do You Use It? por Richard Carrier
Referencias
- Diccionarios Oxford-Complutense. Matemáticas de Christopher Clapham 84-89784-566
- Bayes, Thomas (1763). «An Essay towards solving a Problem in the Doctrine of Chances.». Philosophical Transactions of the Royal Society of London 53: 370-418. doi:10.1098/rstl.1763.0053.
- Jeffreys, Sir Harold (1973). Inferencia científica. (en inglés). Cambridge: At the University Press. OCLC 764571529.
- Frame, Paul (2015). El apóstol de la libertad. Gales: Prensa de la Universidad de Gales. p. 44. ISBN 978-1-78316-216- 1. Consultado el 23 de febrero de 2021.
- Allen, Richard (1999). google.com/books? id=NCu6HhGlAB8C&pg=PA243 David Hartley on Human Nature. SUNY Press. pp. 243-4. ISBN 978-0-7914-9451-6. Consultado el 16 de junio de 2013.
- Bayes, Thomas; Price, Richard (1763). «Un ensayo para resolver un problema de la doctrina del azar. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S.». Philosophical Transactions of the Royal Society of London 53: 370-418.
- Holland, pp. 46-7.
- Price, Richard (1991). Price: Escritos políticos. Cambridge University Press. p. xxiii. ISBN 978-0-521-40969-8. Consultado el 16 de junio de 2013.
- Mitchell, 1911, p. 314.
- Daston, Lorraine (1988). Probabilidad clásica en la Ilustración. Princeton Univ Press. p. 268. ISBN 0-691-08497-1.
- Stigler, Stephen M. (1986). «Inverse Probability». La Historia de la Estadística: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 99-138. ISBN 978-0-674-40341-3.
- Jeffreys, Harold (1973). Inferencia científica (3rd edición). Cambridge University Press. p. 31. ISBN 978-0-521-18078-8.
- Stigler, Stephen M. (1983). «¿Quién descubrió el teorema de Bayes?». The American Statistician 37 (4): 290-296.
- de Vaux, Richard; Velleman, Paul; Bock, David (2016). Stats, Datos y Modelos (4ª edición). Pearson. pp. 380-381. ISBN 978-0-321-98649-8.
- Edwards, A. W. F. (1986). «¿Es la referencia en Hartley (1749) a la inferencia bayesiana?». The American Statistician 40 (2): 109-110. doi:10.1080/00031305.1986.10475370.
- Hooper, Martyn (2013). «Richard Price, el teorema de Bayes y Dios». Significance 10 (1): 36-39. S2CID 153704746. doi:10.1111/j.1740-9713.2013.00638.x.
- McGrayne, S. B. (2011). La teoría que no moriría: Cómo la regla de Bayes descifró el código Enigma, cazó submarinos rusos y emergió triunfante de dos siglos de controversia. Yale University Press. ISBN 978-0-300-18822-6. (requiere registro).
- Parzen, Emanuel. Teoría moderna de probabilidades y sus aplicaciones. Limusa Grupo Noriega Editores. ISBN 978-9681-807351.
- Kraft, Stephanie A.; Duenas, Devan; Wilfond, Benjamin S.; Goddard, Katrina A.B. (de abril de 2019). «The evolving landscape of expanded carrier screening: challenges and opportunities». Genetics in Medicine 21 (4): 790-797. PMID 30245516. doi:10.1038/s41436-018-0273-4.
Bibliografía adicional
- Grunau, Hans-Christoph (24 January 2014). "Preface Issue 3/4-2013". Jahresbericht der Deutschen Mathematiker-Vereinigung. 115 (3–4): 127–128. doi:10.1365/s13291-013-0077-z.
- Gelman, A, Carlin, JB, Stern, HS, and Rubin, DB (2003), "Bayesian Data Analysis," Second Edition, CRC Press.
- Grinstead, CM and Snell, JL (1997), "Introduction to Probability (2nd edition)," American Mathematical Society (free pdf available) [1].
- "Bayes formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- McGrayne, SB (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. Yale University Press. ISBN 978-0-300-18822-6.
- Laplace, Pierre Simon (1986). "Memoir on the Probability of the Causes of Events". Statistical Science. 1 (3): 364–378. doi:10.1214/ss/1177013621. JSTOR 2245476.
- Lee, Peter M (2012), "Bayesian Statistics: An Introduction," 4th edition. Wiley. ISBN 978-1-118-33257-3.
- Puga JL, Krzywinski M, Altman N (31 March 2015). "Bayes' theorem". Nature Methods. 12 (4): 277–278. doi:10.1038/nmeth.3335. PMID 26005726.
- Rosenthal, Jeffrey S (2005), "Struck by Lightning: The Curious World of Probabilities". HarperCollins. (Granta, 2008. ISBN 9781862079960).
- Stigler, Stephen M. (August 1986). "Laplace's 1774 Memoir on Inverse Probability". Statistical Science. 1 (3): 359–363. doi:10.1214/ss/1177013620.
- Stone, JV (2013), download chapter 1 of "Bayes' Rule: A Tutorial Introduction to Bayesian Analysis", Sebtel Press, England.
- Bayesian Reasoning for Intelligent People, An introduction and tutorial to the use of Bayes' theorem in statistics and cognitive science.
- Morris, Dan (2016), Read first 6 chapters for free of "Bayes' Theorem Examples: A Visual Introduction For Beginners" Blue Windmill ISBN 978-1549761744. A short tutorial on how to understand problem scenarios and find P(B), P(A), and P(B|A).
Enlaces externos
- Visual explanation of Bayes using trees en YouTube.
- Bayes' frequentist interpretation explained visually en YouTube.
- Earliest Known Uses of Some of the Words of Mathematics (B). Contains origins of "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", and "Bayes Factor".
- A tutorial on probability and Bayes' theorem devised for Oxford University psychology students
- An Intuitive Explanation of Bayes' Theorem by Eliezer S. Yudkowsky
- Bayesian Clinical Diagnostic Model