Teorema de Casey
En geometría, el teorema de Casey es una generalización del teorema de Ptolomeo, llamado así por el matemático irlandés John Casey (1820-1891).[1]
Formulación del teorema
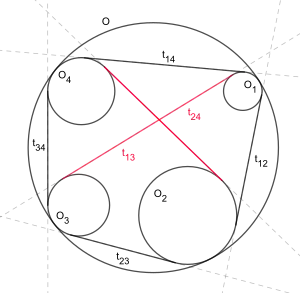
Sea un círculo de radio , y sean (en ese orden) cuatro círculos que no se cortan entre sí, situados dentro de y tangentes a él. Denominando a la longitud de la tangente exterior común de los círculos , entonces:
Nótese que el caso degenerado, donde los cuatro círculos se reducen a puntos, es exactamente el teorema de Ptolomeo.
Notas
- Casey, J. (1866). «On the Equations and Properties: (1) of the System of Circles Touching Three Circles in a Plane; (2) of the System of Spheres Touching Four Spheres in Space; (3) of the System of Circles Touching Three Circles on a Sphere; (4) of the System of Conics Inscribed to a Conic, and Touching Three Inscribed Conics in a Plane». Proceedings of the Royal Irish Academy 9: 396-423. JSTOR 20488927.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.