Teorema de Commandino
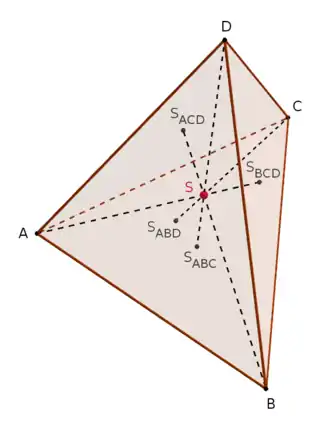
El teorema de Commandino, que lleva el nombre de Federico Commandino (1509–1575), afirma que las cuatro medianas de un tetraedro son concurrentes en un punto S, que las divide en una proporción de 3:1. En un tetraedro, una mediana es un segmento de línea que conecta un vértice con el centroide de la cara opuesta, es decir, el centroide del triángulo opuesto. El punto S se conoce como el centroide del tetraedro.[1][2][3]
El teorema se atribuye a Commandino, quien afirmó en su trabajo De Centro Gravitatis Solidorum (El centro de gravedad de los sólidos, 1565), que las cuatro medianas del tetraedro son concurrentes. Sin embargo, según el erudito del siglo XIX Guillaume Libri, Francesco Maurolico (1494-1575) afirmó haber encontrado el resultado antes. Libri de todas maneras pensó que Leonardo da Vinci lo había conocido incluso antes, y parecía haberlo usado en su trabajo. Julian Coolidge compartió esa evaluación, pero señaló que no podía encontrar ninguna descripción explícita o tratamiento matemático del teorema en las obras de da Vinci.[4] Otros eruditos han especulado que el resultado ya podría haber sido conocido por los matemáticos griegos desde la antigüedad.[5]
Referencias
- Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey: Solid Geometry in the 21st Century. The Mathematical Association of America, 2015, ISBN 9780883853580, pp. 97–98
- Nathan Altshiller-Court: The Tetrahedron and Its Circumscribed Parallelepiped. The Mathematics Teacher, Vol. 26, No. 1 (JANUARY 1933), pp. 46–52 (JSTOR)
- Norman Schaumberger: Commandino's theorem. The Two-Year College Mathematics Journal, Vol. 13, No. 5 (Nov., 1982), p. 331 (JSTOR)
- Nathan Altshiller Court: Notes on the centroid. The Mathematics Teacher, Vol. 53, No. 1 (JANUARY 1960), pp. 34 (JSTOR)
- Howard Eves: Great Moments in Mathematics (before 1650). MAA, 1983, ISBN 9780883853108, p. 225
Enlaces externos
- Esta obra contiene una traducción derivada de «Commandino's Theorem» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Weisstein, Eric W. «Commandino's Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- A Couple of Nice Extensions of the Median Properties