Teorema de Desargues

En geometría proyectiva, el teorema de Desargues, llamado así en honor al geómetra y arquitecto francés Gérard Desargues (1591-1661) que lo enunció en 1638,[1] expone:

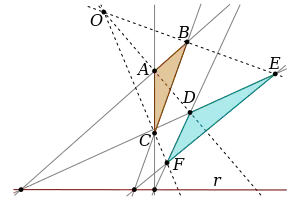
En el plano proyectivo, dos triángulos son proyectivos desde un punto si y solo si son proyectivos desde una recta.

Considere los triángulos ABC y DEF. El que los triángulos sean proyectivos desde un punto significa que las rectas AD, BE y CF concurren en un mismo punto O. De modo parecido, el que los triángulos sean proyectivos desde una recta significa que los pares de lados (AB, DE), (BC, EF) y (AC, DF) se cortan respectivamente sobre una misma recta r.

Al punto O se le llama centro de perspectiva y a la recta r, eje de perspectiva.

Demostración
Demostración
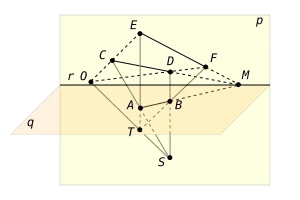Para demostrar este teorema, considere los planos p y q secantes en la recta r. Sea AB un segmento sobre el plano q y M la intersección de la recta AB con la recta r. Sean S y T dos puntos exteriores a dichos planos. Sean C y D las proyecciones sobre el plano p de los puntos A y B desde el punto S y E y F las proyecciones del mismo segmento AB desde el punto T sobre el plano p.

El plano determinado por los puntos SAB corta al plano p sobre la recta CD. El punto M se encuentra sobre el dicho plano, por estar sobre la recta AB y por esta razón M se halla sobre la recta CD. Usando los mismos argumentos, pero considerando ahora el plano TAB, se demuestra que el punto M es común a las rectas AB y EF. Así, las rectas CD y EF se cortan en el mismo punto M sobre la recta r.

Sea O la intersección de la recta ST sobre el plano p. El plano STA corta al plano p sobre la recta CE que contiene al punto O. De manera similar, el plano STB corta al plano p en la recta DF que también contiene al punto O. Por tanto, las rectas CE y DF se cortan en dicho punto.

De modo que los pares de puntos C, E y D, F son proyectivos desde el punto O. Las rectas CD y EF son proyectivas desde la recta r.

El recíproco también es cierto: Si las rectas CD y EF pertenecen al mismo plano p, son proyectivas desde una recta r y los puntos correspondientes C, E y D, F son proyectivos desde un punto O en dicho plano, entonces existe un plano q, secante al plano p en r, una recta AB sobre dicho plano y un par de puntos exteriores a ambos planos desde los cuales la recta AB se proyecta sobre CD y EF, el punto A sobre C y E, y el punto B sobre D y F.

En el teorema de Desargues, podemos considerar los triángulos como las proyecciones de un único triángulo sobre algún plano q desde dos puntos distintos S y T. La recta r y el punto O son respectivamente, la intersección del plano q con aquel donde los dos triángulos son proyectivos y la intersección de la recta ST con aquel plano. Los vértices correspondientes en ambos triángulos serán proyectivos desde el punto O y los lados correspondientes de ambos triángulos serán proyectivos desde la recta r. Esto demuestra el teorema.

Véase también

Referencias
  1. Œuvres de Desargues, Première proposition géométrique, aperçu, p. 413, en Google Libros, extraído de la perspectiva de Bosse (1648).

Bibliografía
  • Luigi Cremona, Elements of Projective Geometry 3rd. edition, Dover 2005 ISBN 0-486-44266-7
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.