Segundo teorema de Shannon

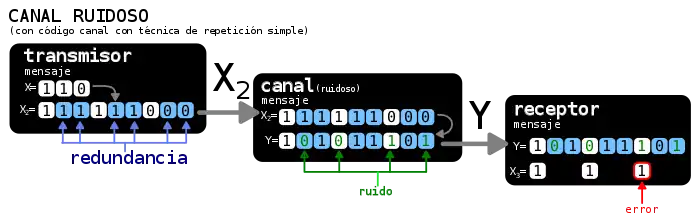
Una de las principales ventajas de la tecnología digital es que permite el intercambio de datos sin pérdida de información. Aun así, estos datos transitan la mayoría del tiempo sobre canales no fiables, sufriendo varias interferencias y por lo tanto se mezclan con el ruido. Entonces, ¿cómo se pueden eliminar los errores de transmisión? La solución consiste en introducir cierta redundancia en los mensajes emitidos por la fuente con el fin de que el receptor pueda corregir los errores, de tal forma que el mensaje sea compuesto por ${\displaystyle n+k}$ símbolos, en donde ${\displaystyle n}$ es la cantidad de símbolos que aportan información sobre el mensaje original (aquel que el emisor transmitió), y ${\displaystyle k}$ es la cantidad de símbolos de redundancia, mismos que le servirán al receptor para corregir los errores que el canal ruidoso haya introducido en el mensaje, cabe recordar que estos ${\displaystyle k}$ símbolos de redundancia también están sujetos a deformaciones debido al ruido del canal. A este tipo de código se le llama código corrector.

El Segundo Teorema de Shannon demuestra la existencia de un código corrector cuyo ${\displaystyle k}$ cumple lo dicho anteriormente, con una probabilidad de interpretar un mensaje de forma errada muy pequeña, y con una velocidad de transmisión que se aproxima a la capacidad del canal.

El tiempo necesario para enviar un símbolo por la línea r, el símbolos llamado. Dentro de la símbolos la señal sigue siendo el mismo.

${\displaystyle N_{bits}=\log _{2}(N_{symbols})}$

Con dos símbolos definidos (Nsymbols = 2), por lo tanto, _Nsymbols transportados, en 8-PSK tres bits y en QAM-64, seis bits.

La unidad para medir el número de símbolos por segundo es el baudio.

Teorema (Shannon, 1948):

1. Para cualquier canal discreto sin memoria, la capacidad de canal.[2]

${\displaystyle \ C=\sup _{p_{X}}I(X;Y)\,}$.[3][4]

Tiene la siguiente propiedad. Para cualquier ε> 0 y R <C, para N bastante grande, existe un código de longitud N y una tasa ≥ R y un algoritmo de descodificación, de forma que la probabilidad máxima de error de bloque es ≤ ε.

2. Si la probabilidad de error de bits pb es aceptable, las tasas de transmisión hasta R (pb) son alcanzables, donde

${\displaystyle R(p_{b})={\frac {C}{1-H_{2}(p_{b})}}.}$

y ${\displaystyle H_{2}(p_{b})}$ es la función entropía binaria

${\displaystyle H_{2}(p_{b})=-\left[p_{b}\log _{2}{p_{b}}+(1-p_{b})\log _{2}({1-p_{b}})\right]}$

3. Para cualquier pb, las tasas de transmisión más grandes que R (pb) no son alcanzables.

(MacKay (2003), p. 162; de Gallager (1968), ch.5; Cover and Thomas (1991), p. 198; Shannon (1948) thm. 11)

• Paradoja de Freedman
• Desigualdad de Jensen
• Teorema de codificación de fuentes de Shannon
• Teorema de Shannon-Hartley

• Cover T. M., Thomas J. A., Elementos of Information Theory, John Wiley & Sonidos, 1991. ISBN 0-471-06259-6
• Fano, R. A., Transmission of information; a statistical theory of communications, MIT Press, 1961. ISBN 0-262-06001-9
• Feinstein, Amiel, "A New basic theorem of information theory", IEEE Transactions donde Information Theory, 4(4): 2-22, 1954.
• MacKay, David J. C., Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003. ISBN 0-521-64298-1 [free online]
• Shannon, C. E., A Mathematical Theory of Communication Archivado el 31 de enero de 1998 en Wayback Machine. Urbana, IL: University of Illinois Press, 1949 (reprinted 1998).
• Wolfowitz, J., "The coding of messages subject tono chance errores", Illinois J. Math., 1: 591–606, 1957.

• Esta obra contiene una traducción derivada de «Segon teorema de Shannon» de Wikipedia en catalán, concretamente de esta versión del 17 de junio de 2017, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
• Esta obra contiene una traducción derivada de «Deuxième théorème de Shannon» de Wikipedia en francés, concretamente de esta versión del 3 de marzo de 2017, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
• Esta obra contiene una traducción derivada de «Noisy-channel coderings theorema» de Wikipedia en neerlandés, concretamente de esta versión del 10 de marzo de 2013, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
• CE Shannon, "A Mathematical Theory of Communication", Bello System Technical Journal, vol. 27, pp. 379-423, julio de 1948.
• Donde Shannon and Shannon's law. Archivado el 15 de marzo de 2016 en Wayback Machine.
• Shannon's Noisy Channel Coding Theorem.