Teorema japonés para cuadriláteros cíclicos

En geometría, el teorema japonés establece que los centros de las circunferencias inscritas de ciertos triángulos dentro de un cuadrilátero cíclico son los vértices de un rectángulo.

M₁M₂M₃M₄ es un rectángulo.

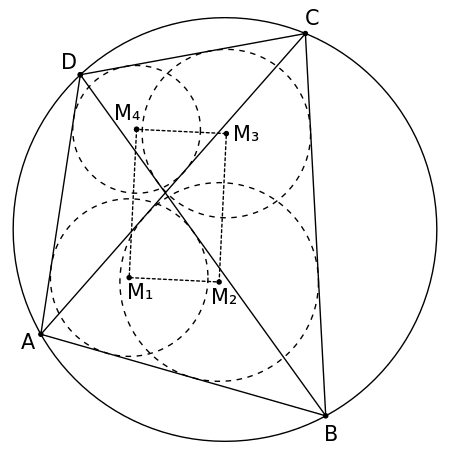
Triangular un cuadrilátero cíclico arbitrario por sus diagonales produce cuatro triángulos superpuestos (cada diagonal crea dos triángulos). Los centros de los círculos de esos triángulos forman un rectángulo.

Específicamente, sea ABCD un cuadrilátero cíclico arbitrario, y sean M_1, M_2, M_{3, y} M₄ los centros de los triángulos △ABD, △ABC, △BCD, △ACD. Entonces, el cuadrilátero formado por M_1, M_2, M_{3, y} M₄ es un rectángulo.

Téngase en cuenta que este teorema se extiende fácilmente para probar el teorema japonés para polígonos cíclicos. Para probar el caso del cuadrilátero, basta con construir el paralelogramo tangente a las esquinas del rectángulo construido, con lados paralelos a las diagonales del cuadrilátero. La construcción muestra que el paralelogramo es un rombo, lo que equivale a mostrar que las sumas de los radios de los incírculos tangentes a cada diagonal son iguales.

El caso del cuadrilátero demuestra inmediatamente el caso general por inducción en el conjunto de particiones trianguladas de un polígono general.