Transformación divisoria
Una imagen en escala de grises puede ser vista como un relieve topográfico, donde se interpreta el nivel de gris de un píxel como su altura en el relieve. Una gota de agua que cae sobre un relieve topográfico fluye a lo largo de un camino para finalmente llegar a un mínimo local. Intuitivamente, la divisoria de un relieve corresponde a los límites de las cuencas hidrográficas adyacentes.
En el procesamiento de imágenes se pueden calcular diversas líneas divisorias. En los grafos algunas pueden ser definidas sobre los nodos, las aristas o líneas híbridas sobre los nodos y aristas. Las divisorias también se puede definir en el dominio continuo.[1] También hay muchos algoritmos diferentes para calcular las divisorias.
Para un propósito de segmentación de imágenes, la longitud del gradiente se interpreta como información de elevación.
 Imagen del gradiente
Imagen del gradiente Relieve del gradiente
Relieve del gradiente
 Divisorias del gradiente
Divisorias del gradiente Divisorias del gradiente (relieve)
Divisorias del gradiente (relieve)
Clasificación
Divisoria por inundación
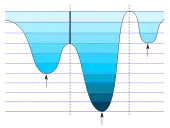
La idea fue introducida en 1979 por S. Beucher y C. Lantuéjoul en.[2] Consiste en colocar una fuente de agua en cada mínimo regional para inundar el relieve desde las fuentes y construir barreras donde las distintas fuentes se unen. El conjunto resultante de barreras constituye una divisoria por inundación.
Divisoria por distancia topográfica
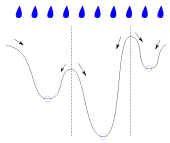
Intuitivamente, una gota de agua que cae sobre un relieve topográfico fluye más rápidamente hacia un mínimo. En la clase anterior no se verifica esta condición.
Divisoria inter-pixel
S. Beucher y F. Meyer introdujeron en[3] una definición algorítmica de la divisoria inter-pixel, dando el siguiente procedimiento:
1. Etiquete cada mínimo con una etiqueta distinta. Inicialice un conjunto S con los nodos etiquetados.
2. Extraiga de S un nodo x de mínima altitud F, es decir, F(x) = min{F(y)|y en S}. Asigne la etiqueta de x a cada nodo y no etiquetado adyacente a x, e inserte y en S.
3. Repita el paso 2 hasta que S esté vacío.
Divisoria topológica
Las nociones anteriores se centran en las cuencas, pero no en la línea de separación producida. La divisoria topológica fue introducida por M. Couprie y G. Bertrand en 1997.[4] Se beneficia de la siguiente propiedad fundamental: una función W es una divisoria de una función F (F es una función que asigna pesos en las aristas de la gráfica asociada a la imagen) si y solo si W ≤ F y W conserva el contraste entre los mínimos regionales de F, donde el contraste entre dos mínimos regionales M1 y M2 se define como la altura mínima a la que hay que subir para ir de M1 a M2.[5]
Algoritmos
Diversos enfoques pueden ser empleados para utilizar el principio de la divisoria para la segmentación de imágenes:
- Los mínimos locales del gradiente de la imagen pueden ser elegidos como marcadores, en este caso se produce una excesiva segmentación y un segundo paso implica la fusión de regiones.
- La transformación divisoria basada en marcadores hace uso de posiciones de marcadores específicos que han sido ya sea explícitamente definidos por el usuario o determinados de forma automática con operadores morfológicos o de otras formas.
Algoritmo de inundación de Meyer
Uno de los algoritmos de divisoria más común fue presentado por F. Meyer en los años 90.
El algoritmo funciona sobre una imagen en escala de grises. Durante las inundaciones sucesivas del relieve con valores de gris, las divisorias con cuencas adyacentes se construyen. Este proceso de inundaciones se lleva a cabo en la imagen del gradiente, es decir, las cuencas deben surgir a lo largo de los bordes. Normalmente, esto dará lugar a un exceso de segmentación de la imagen, especialmente para imágenes con ruido, por ejemplo, una TAC. O bien la imagen debe ser preprocesada o las regiones deben ser fusionadas después sobre la base de un criterio de similitud.
Pasos:
- Un conjunto de marcadores, los píxeles donde la inundación se iniciará, son elegidos. Cada uno recibe una etiqueta diferente.
- Los píxeles vecinos de cada zona marcada se insertan en una cola de prioridad con un nivel de prioridad correspondiente al nivel de gris de los píxeles.
- El píxel con el nivel de prioridad más alto se extrae de la cola de prioridad. Si todos los vecinos del píxel extraído que ya han sido etiquetados tienen la misma etiqueta, entonces el píxel es marcado con su etiqueta. Todos los vecinos no marcados que aún no están en la cola de prioridad se colocan en la cola de prioridad.
- Rehacer el paso 3 hasta que la cola de prioridad esté vacía.
Los píxeles no-etiquetados son las líneas divisorias.
Algoritmos bosque de expansión óptimo (watershed cuts)
Las divisorias como bosque de expansión óptimo han sido introducidas por Jean Cousty et al.[6] Ellos establecieron la compatibilidad de estas divisorias: pueden ser definidas equivalentemente por sus "cuencas de captación" (a través de la propiedad de descenso más rápido) o por la "línea divisoria" que separa las cuencas (a través del principio de la caída del agua). Luego, ellos prueban, a través de un teorema de equivalencia, su optimalidad en términos de bosques de expansión mínimo. Después, introducen un algoritmo de tiempo lineal para calcularlas. Vale la pena señalar que propiedades similares no se verifican en otros marcos y que el algoritmo propuesto es el algoritmo más eficiente existente, tanto en la teoría como en la práctica.
 Una imagen con dos marcadores (verdes) y un bosque de expansión mínimo calculado sobre el gradiente de la imagen.
Una imagen con dos marcadores (verdes) y un bosque de expansión mínimo calculado sobre el gradiente de la imagen. Resultado de la segmentación por bosque de expansión mínimo.
Resultado de la segmentación por bosque de expansión mínimo.
Vínculos con otros algoritmos de visión por computador
Graph Cuts
En 2007, C. Allène et al.[7] establecieron vínculos que relacionan graph cuts a los bosques de expansión óptima. Más precisamente, muestran que cuando la potencia de los pesos del grafo está por encima de un cierto número, el corte que minimiza la energía de los graph cuts es un corte por bosques de expansión máxima.
Bosques de camino más corto
La image foresting transform (IFT) de Falcao et al.[8] es un procedimiento para calcular bosques de caminos más cortos. J. Cousty et al.[9] demostraron que cuando los marcadores de la IFT corresponden a extremos de la función peso, el corte inducido por el bosque es un watershed cut.
Random Walker
El algoritmo random walker es un algoritmo de segmentación que resuelve el problema de Dirichlet, adaptado para segmentación de imágenes por L. Grady en 2006.[10] En 2009, C. Couprie et al. demostraron que cuando el poder de los pesos del grafo convergen hacia el infinito, el corte que minimiza la energía del random walker es un corte por bosque de expansión máxima.[11]
Jerarquías
Una transformación jerárquica de divisorias transforma el resultado en un despliegue gráfico (es decir, se determinan las relaciones de vecindad de las regiones segmentadas) y aplica después transformaciones divisorias de forma recursiva.
Referencias
- L. Najman and M. Schmitt. Watershed of a continuous function. In Signal Processing (Special issue on Mathematical Morphology.), Vol. 38 (1994), pages 99–112
- Serge Beucher and Christian Lantuéjoul. Use of watersheds in contour detection. In International workshop on image processing, real-time edge and motion detection (1979). http://cmm.ensmp.fr/~beucher/publi/watershed.pdf
- Serge Beucher and Fernand Meyer. The morphological approach to segmentation: the watershed transformation. In Mathematical Morphology in Image Processing (Ed. E.R. Dougherty), pages 433-481 (1993).
- M. Couprie, G. Bertrand. Topological gray-scale watershed transform. In Proc. of SPIE Vision Geometry V, volume 3168, pages 136-146 (1997). http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.3.7654&rep=rep1&type=pdf
- G. Bertrand. On topological watersheds. Journal of Mathematical Imaging and Vision, 22(2-3), pages 217–230 (2005).
- Jean Cousty, Gilles Bertrand, Laurent Najman, and Michel Couprie. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle. IEEE Transactions on Pattern Analysis and Machine Intelligence. 31 (8). August 2009. pp. 1362–1374.
- Cédric Allène, Jean-Yves Audibert, Michel Couprie and Renaud Keriven: "Some links between min-cuts, optimal spanning forests and watersheds", Image and Vision Computing, 2009.
- Falcao, A.X. Stolfi, J. de Alencar Lotufo, R.: "The image foresting transform: theory, algorithms, and applications", In PAMI, 2004
- Jean Cousty, Gilles Bertrand, Laurent Najman, and Michel Couprie. Watershed cuts: thinnings, shortest-path forests and topological watersheds. IEEE Transactions on Pattern Analysis and Machine Intelligence. 32 (5). 2010. pp. 925–939.
- Grady, L.: Random walks for image segmentation. PAMI, 2006
- C. Couprie, L. Grady, L. Najman and H. Talbot, "Power Watersheds: A New Image Segmentation Framework Extending Graph Cuts, Random Walker and Optimal Spanning Forest", ICCV 2009
- Fernand Meyer. Un algorithme optimal pour la ligne de partage des eaux. Dans 8me congrès de reconnaissance des formes et intelligence artificielle, Vol. 2 (1991), pages 847-857, Lyon, France.
- Luc Vincent and Pierre Soille. Watersheds in digital spaces: an efficient algorithm based on immersion simulations. In IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 13, Num. 6 (1991), pages 583-598.
- L. Najman and M. Schmitt. Geodesic saliency of watershed contours and hierarchical segmentation. In IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 18, Num. 12 (1996), pages 1163-1173.
- J.B.T.M. Roerdink and A. Meijster. The watershed transform: definitions, algorithms, and parallelization strategies. In Fundamenta Informaticae 41 (2000), pp. 187–228.
- Laurent Najman, Michel Couprie and Gilles Bertrand. Watersheds, mosaics, and the emergence paradigm. In Discrete Applied Mathematics, Vol. 147, Num. 2-3(2005), Pages 301-324.
Enlaces externos
- The Watershed Transformation con animaciones del algoritmo divisorio.
- Topological Watershed Transform con artículos, diapositivas de clases y código fuente.
- An open source watershed plugin para ImageJ.
- An introduction of principle among other segmentation algorithms
- A presentation of the Image Foresting transform, based on shortest path forests