Transición Vítrea
La transición vítreo-líquido, o transición vítrea, es la transición gradual y reversible en materiales amorfos (o en regiones amorfas dentro de materiales semicristalinos), desde un estado "vítreo" duro y relativamente quebradizo a un estado viscoso o gomoso a medida que aumenta la temperatura.[1] Un sólido amorfo que muestra una transición vítrea se llama vidrio. La transición inversa, que se logra al enfriar demasiado un líquido viscoso en el estado de vidrio, se llama vitrificación.
La temperatura de transición vítrea Tg de un material caracteriza el rango de temperaturas en el que se produce esta transición vítrea. Siempre es más baja que la temperatura de fusión, Tm, del estado cristalino del material, si existe.
Los plásticos duros como el poliestireno y el poli (metacrilato de metilo) se usan muy por debajo de sus temperaturas de transición vítrea, es decir, cuando están en su estado vítreo. Sus valores de Tg están muy por encima de la temperatura ambiente, ambos a unos 100 °C (212 °F). Los elastómeros de caucho como el poliisopreno y el poliisobutileno se utilizan por encima de su Tg, es decir, en el estado gomoso, donde son suaves y flexibles.[2]
A pesar del cambio en las propiedades físicas de un material a través de su transición vítrea, la transición no se considera una transición de fase; más bien es un fenómeno que se extiende sobre un rango de temperatura y está definido por una de varias convenciones.[3][4] Dichas convenciones incluyen una velocidad de enfriamiento constante (20 kelvins por minuto (36 °F/min)).[1] y un umbral de viscosidad de 1012 Pa · s, entre otros. Al enfriarse o calentarse a través de este rango de transición vítrea, el material también muestra un paso suave en el coeficiente de expansión térmica y en el calor específico, y la ubicación de estos efectos depende nuevamente de la historia del material.[5] La cuestión de si alguna transición de fase subyace a la transición vítrea es una cuestión de investigación continua.[3][4][6]
Definición de IUPAC
Transición vítrea (en la ciencia de los polímeros): Proceso en el que un polímero fundido cambia al enfriarse a un vidrio polimérico o un vidrio polimérico cambia al calentarse a un polímero fundido.[7] Note 1: Los fenómenos que se producen en la transición vítrea de los polímeros siguen siendo objeto de investigación y debate científicos en curso. La transición vítrea presenta características de una transición de segundo orden ya que los estudios térmicos a menudo indican que las energías molares de Gibbs, las entalpías molares y los volúmenes molares de las dos fases, es decir, el fundido y el vidrio, son iguales, mientras que la capacidad de calor y la expansividad son discontinuas. Sin embargo, la transición vítrea no se considera generalmente como una transición termodinámica en vista de la dificultad inherente para alcanzar el equilibrio en un vidrio polimérico o en un polímero fundido a temperaturas cercanas a la temperatura de transición vítrea. Note 2: En el caso de los polímeros, los cambios de conformación de los segmentos, que consisten normalmente en 10-20 átomos de la cadena principal, se vuelven infinitamente lentos por debajo de la temperatura de transición vítrea. Note 3: En un polímero parcialmente cristalino, la transición vítrea se produce sólo en las partes amorfas. del material. Note 4: La definición es diferente a la de ref.[8] Note 5: No se recomienda el término comúnmente utilizado "transición vítreo-goma" para la transición vítrea.[9] |
Introducción
La transición vítrea de un líquido a un estado sólido puede ocurrir por enfriamiento o compresión.[10] La transición comprende un aumento suave de la viscosidad de un material en hasta 17 órdenes de magnitud dentro de un rango de temperatura de 500 K sin ningún cambio pronunciado en la estructura del materia.[11] La consecuencia de este aumento dramático es un vidrio que exhibe propiedades mecánicas sólidas en la escala de tiempo de la observación práctica. Esta transición contrasta con la transición de congelación o cristalización, que es una transición de fase de primer orden en la clasificación de Ehrenfest e implica discontinuidades en las propiedades termodinámicas y dinámicas como el volumen, la energía y la viscosidad. En muchos materiales que normalmente se someten a una transición de congelación, el enfriamiento rápido evitará esta transición de fase y en cambio dará como resultado una transición de vidrio a una temperatura más baja. Otros materiales, como muchos polímeros, carecen de un estado cristalino bien definido y forman vidrios fácilmente, incluso con enfriamiento o compresión muy lentos. La tendencia a que un material forme un vidrio mientras está apagado se llama capacidad de formación de vidrio. Esta capacidad depende de la composición del material y puede predecirse mediante la teoría de la rigidez.[12]
Por debajo del rango de temperatura de transición, la estructura vítrea no se relaja de acuerdo con la velocidad de enfriamiento utilizada. El coeficiente de expansión para el estado vítreo es aproximadamente equivalente al del sólido cristalino. Si se utilizan velocidades de enfriamiento más lentas, el mayor tiempo para que ocurra la relajación estructural (o la reorganización intermolecular) puede dar lugar a un producto de vidrio de mayor densidad. De manera similar, al recocer (y por lo tanto permitir una relajación estructural lenta), la estructura de vidrio se aproxima en el tiempo a una densidad de equilibrio correspondiente al líquido sobreenfriado a esta misma temperatura. Tg se encuentra en la intersección entre la curva de enfriamiento (volumen versus temperatura) para el estado vítreo y el líquido sobreenfriado.[13][14][15][16][17]
La configuración del vidrio en este rango de temperatura cambia lentamente con el tiempo hacia la estructura de equilibrio. El principio de la minimización de la energía libre de Gibbs proporciona la fuerza de conducción termodinámica necesaria para el cambio eventual. Cabe señalar aquí que a temperaturas algo más altas que la Tg, la estructura correspondiente al equilibrio a cualquier temperatura se logra con bastante rapidez. En contraste, a temperaturas considerablemente más bajas, la configuración del vidrio permanece sensiblemente estable durante períodos de tiempo cada vez más prolongados.
Por lo tanto, la transición líquido-vidrio no es una transición entre estados de equilibrio termodinámico. Se cree ampliamente que el verdadero estado de equilibrio es siempre cristalino. Se cree que el vidrio existe en un estado cinéticamente cerrado, y su entropía, densidad, etc., dependen de la historia térmica. Por lo tanto, la transición vítrea es ante todo un fenómeno dinámico. El tiempo y la temperatura son cantidades intercambiables (en cierta medida) cuando se trata de vidrios, un hecho que a menudo se expresa en el principio de superposición tiempo-temperatura. Al enfriar un líquido, los grados internos de libertad se desequilibran sucesivamente. Sin embargo, existe un debate de larga data sobre si existe una transición de fase de segundo orden subyacente en el límite hipotético de tiempos de relajación infinitamente largos.[18][19][20]
Temperatura de transición Tg

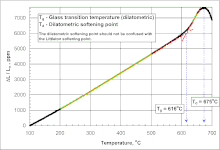
Consulte la figura de la derecha que representa la capacidad calorífica en función de la temperatura. En este contexto, Tg es la temperatura correspondiente al punto A en la curva. Las secciones lineales debajo y arriba de Tg son de color verde. Tg es la temperatura en la intersección de las líneas de regresión rojas.[21]
Se están utilizando diferentes definiciones operativas de la temperatura de transición vítrea Tg, y varias de ellas están aprobadas como estándares científicos aceptados. Sin embargo, todas las definiciones son arbitrarias, y todas producen resultados numéricos diferentes: en el mejor de los casos, los valores de Tg para una sustancia determinada concuerdan dentro de unos pocos kelvins. Una definición se refiere a la viscosidad, fijando Tg en un valor de 1013 poises (o 1012 Pa·s). Como se demostró experimentalmente, este valor está cerca del punto de recocido de muchos vidrios.[22]
En contraste con la viscosidad, la expansión térmica, la capacidad térmica, el módulo de corte y muchas otras propiedades de los vidrios inorgánicos muestran un cambio relativamente repentino a la temperatura de transición vítrea. Cualquiera de estos pasos o torceduras se pueden utilizar para definir Tg. Para que esta definición sea reproducible, se debe especificar la velocidad de enfriamiento o calentamiento.
La definición más utilizada de Tg utiliza la liberación de energía al calentar en un calorímetro diferencial de barrido. Normalmente, la muestra se enfría primero a 10 K/min y luego se calienta a esa misma velocidad.
Otra definición más de Tg usa la torsión en la dilatometría (expansión térmica). Aquí, las tasas de calentamiento de 3–5 K/min (5.4–9.0 °F/min) son comunes. A continuación se resumen los valores de Tg característicos de ciertas clases de materiales.
Polímeros
| Material | Tg (°C) | Nombre comercial |
|---|---|---|
| Goma de neumático | -70 °C [23] | |
| Polifluoruro de vinilideno (PVDF) | -35 °C[24] | |
| Polipropileno (PP atáctico) | -20 °C[25] | |
| Fluoruro de polivinilo (PVF) | -20 °C[24] | |
| Polipropileno (PP isotáctico) | 0 °C[25] | |
| Poli-3-hidroxibutirato (PHB) | 15 °C[25] | |
| Poli(Acetato de vinilo) (PVAc) | 30 °C[25] | |
| Policlorotrifluoroetileno (PCTFE) | 45 °C[24] | |
| Poliamida (PA) | 47-60 °C | Nylon-6,x |
| Ácido Politáctico (PLA) | 60-65 °C | |
| Tereftalato de polietileno (PET) | 70 °C[25] | |
| Poli(Cloruro de vinilo) (PVC) | 80 °C[25] | |
| Poli(Alcohol de vinilo) (PVA) | 85 °C[25] | |
| Poliestireno (PS) | 95 °C[25] | |
| Poly(Metacrilato de metilo) (PMMA atactic) | 105 °C[25] | Plexiglas, Perspex |
| Acrilonitrilo butadieno estireno (ABS) | 105 °C[26] | |
| Politetrafluoroetileno (PTFE) | 115 °C[27] | Teflón |
| Poli(Carbonato) (PC) | 145 °C[25] | Lexan |
| Polisulfona | 185 °C | |
| Polinorborneno | 215 °C[25] |
El nylon-6 seco tiene una temperatura de transición vítrea de 47 °C (117 °F).[28] El nylon-6,6 en estado seco tiene una temperatura de transición vítrea de aproximadamente 70 °C (158 °F).[29][30] Mientras que el polietileno tiene un rango de transición vítrea de −130 - −80 °C (−202 - −112 °F) [31] Lo anterior son solo valores medios, ya que la temperatura de transición vítrea depende de la velocidad de enfriamiento y la distribución de pesos moleculares y podría Estar influenciado por los aditivos. Para un material semicristalino, como el polietileno que es 60–80% cristalino a temperatura ambiente, la transición vítrea citada se refiere a lo que sucede con la parte amorfa del material al enfriarse.
Silicatos y otros vidrios de red covalentes
| Material | Tg (°C) |
|---|---|
| Calcogenuro GeSbTe | 150 °C[32] |
| Calcogenuro AsGeSeTe | 245 °C |
| ZBLAN Vidrio de fluoruro | 235 °C |
| Dióxido de telurio | 280 °C |
| Fluoroaluminato | 400 °C |
| Vidrio común | 520-600 °C |
| Cuarzo fusionado (aproximado) | 1200 °C[33] |
Paradoja de Kauzmann
A medida que se sobre enfría el líquido, la diferencia en la entropía entre la fase líquida y la sólida disminuye. Al extrapolar la capacidad térmica del líquido subenfriado por debajo de su temperatura de transición vítrea, es posible calcular la temperatura a la cual la diferencia en entropías se vuelve cero. Esta temperatura ha sido nombrada la temperatura de Kauzmann.
Si un líquido pudiera subenfriarse por debajo de la temperatura de Kauzmann y mostrara una entropía más baja que la fase cristalina, las consecuencias serían paradójicas. Esta paradoja de Kauzmann ha sido objeto de mucho debate y muchas publicaciones desde que Walter Kauzmann la presentó por primera vez en 1948.[34]
Una resolución de la paradoja de Kauzmann es decir que debe haber una transición de fase antes de que disminuya la entropía del líquido. En este escenario, la temperatura de transición se conoce como temperatura de transición vítrea ideal calorimétrica T0c. Según este punto de vista, la transición vítrea no es simplemente un efecto cinético, es decir, es el resultado del enfriamiento rápido de una masa fundida, sino que existe una base termodinámica subyacente para la formación de vidrio. La temperatura de transición vítrea:
El modelo de Gibbs-DiMarzio predice específicamente que la entropía configuracional de un líquido subenfriado desaparece en el límite , donde finaliza el régimen de existencia del líquido, su microestructura se vuelve idéntica a la del cristal, y sus curvas de propiedad se intersecan en una verdadera transición de fase de segundo orden. Esto nunca se ha verificado experimentalmente debido a la dificultad de lograr una velocidad de enfriamiento lo suficientemente lenta, al tiempo que se evita la cristalización accidental.
Resoluciones alternativas
Hay al menos otras tres posibles soluciones a la paradoja de Kauzmann. Podría ser que la capacidad de calor del líquido subenfriado cerca de la temperatura de Kauzmann disminuya suavemente a un valor más pequeño. También podría ser que se produzca una transición de fase de primer orden a otro estado líquido antes de que la temperatura de Kauzmann sea inferior a la capacidad calorífica de este nuevo estado que la obtenida por extrapolación de una temperatura más alta. Finalmente, el propio Kauzmann resolvió la paradoja de la entropía al postular que todos los líquidos sobreenfriados deben cristalizar antes de que se alcance la temperatura de Kauzmann.
En materiales concretos
Sílice, SiO2
La sílice (el compuesto químico SiO2) tiene varias formas cristalinas distintas además de la estructura de cuarzo. Casi todas las formas cristalinas implican unidades tetraédricas de SiO4 unidas entre sí por vértices compartidos en diferentes disposiciones. Las longitudes de los enlaces Si-O varían entre las diferentes formas de cristal. Por ejemplo, en α-cuarzo, la longitud del enlace es de 161 picómetros (6.3 × 10−9 pulgadas), mientras que en α-tridimita varía de 154–171 pm (6.1 × 10−9–6.7 × 10−9 pulgadas). El ángulo de enlace Si-O-Si también varía de 140° en α-tridimita a 144° en α-cuarzo a 180° en β-tridimita. Cualquier desviación de estos parámetros estándar constituye diferencias microestructurales o variaciones que representan una aproximación a un sólido vítreo o amorfo. La temperatura de transición Tg en los silicatos está relacionada con la energía requerida para romper y volver a formar enlaces covalentes en una red de enlaces covalentes amorfa(o red aleatoria). La Tg está claramente influenciada por la química del vidrio. Por ejemplo, la adición de elementos como B, Na, K o Ca a un vidrio de sílice, que tiene una valencia inferior a 4, ayuda a romper la estructura de la red, reduciendo así la Tg. Alternativamente, P, que tiene una valencia de 5, ayuda a reforzar una red ordenada, y por lo tanto aumenta la Tg.[35]
La Tg es directamente proporcional a la resistencia de la unión, por ejemplo. depende de los parámetros termodinámicos de los enlaces de casi equilibrio, p. ej. en la entalpía Hd y entropía Sd de configuraciones - enlaces rotos: Tg = Hd / [Sd + Rln [(1-fc) / fc] donde R es la constante de los gases y fc es el umbral de percolación. Para fundiciones fuertes como el SiO2, el umbral de percolación en la ecuación anterior es la densidad crítica universal de Scher-Zallen en el espacio 3D, por ej. fc = 0.15, sin embargo, para los materiales frágiles, los umbrales de percolación dependen del material y fc << 1.[36] La entalpía y la entropía de las configuraciones - los enlaces rotos se pueden encontrar a partir de los datos experimentales disponibles sobre la viscosidad.[37]

Polímeros
En los polímeros, la temperatura de transición vítrea, Tg, a menudo se expresa como la temperatura a la cual la energía libre de Gibbs es tal que la energía de activación para el movimiento cooperativo de 50 o más elementos del polímero se excede. Esto permite que las cadenas moleculares se deslicen unas sobre otras cuando se aplica una fuerza. La introducción de grupos químicos relativamente rígidos (como los anillos de benceno) interferirá con el proceso de flujo y, por lo tanto, aumentará la Tg.[38] La rigidez de los termoplásticos disminuye debido a este efecto. Cuando se alcanza la temperatura del vidrio, la rigidez permanece igual durante un tiempo, es decir, en o cerca de E2, hasta que la temperatura supera la Tm, y el material se derrite. Esta región se llama la meseta del caucho.
En el planchado, un tejido se calienta a través de esta transición para que las cadenas de polímero se vuelvan móviles. El peso del hierro impone entonces una orientación preferida. La Tg puede reducirse significativamente mediante la adición de plastificantes en la matriz del polímero. Las moléculas más pequeñas de plastificante se insertan entre las cadenas de polímero, lo que aumenta el espacio y el volumen libre, y les permite moverse una a la otra incluso a temperaturas más bajas. La adición de grupos laterales no reactivos a un polímero también puede hacer que las cadenas se separen entre sí, reduciendo la Tg. Si un plástico con algunas propiedades deseables tiene una Tg que es demasiado alta, a veces se puede combinar con otra en un copolímero o material compuesto con una Tg por debajo de la temperatura del uso previsto. Tenga en cuenta que algunos plásticos se utilizan a altas temperaturas, por ejemplo, en motores de automóviles, y otros a bajas temperaturas.[25]

En los materiales viscoelásticos, la presencia de un comportamiento similar al líquido depende de las propiedades y, por lo tanto, varía con la velocidad de la carga aplicada, es decir, con qué rapidez se aplica una fuerza. El juguete de silicona Silly Putty se comporta de manera muy diferente en función del tiempo de aplicación de una fuerza: tire lentamente y fluye, actuando como un líquido muy viscoso; Golpéalo con un martillo y se rompe, actuando como un vidrio.
Al enfriarse, el caucho experimenta una transición de líquido-vidrio, que también se conoce como transición de caucho-vidrio.
Mecánica de vitrificación
El movimiento molecular en la materia condensada se puede representar mediante una serie de Fourier cuya interpretación física consiste en una superposición de ondas longitudinales y transversales de desplazamiento atómico con diferentes direcciones y longitudes de onda. En los sistemas monatómicos, estas ondas se denominan fluctuaciones de densidad. (En los sistemas poliatómicos, también pueden incluir fluctuaciones de composición).[39]
Por lo tanto, el movimiento térmico en líquidos se puede descomponer en vibraciones longitudinales elementales (o fonones acústicos), mientras que las vibraciones transversales (u ondas de corte) se describieron originalmente solo en sólidos elásticos que exhiben el estado cristalino altamente ordenado de la materia. En otras palabras, los líquidos simples no pueden soportar una fuerza aplicada en forma de esfuerzo de cizallamiento y producirán mecánicamente a través de la deformación plástica macroscópica (o flujo viscoso). Además, el hecho de que un sólido se deforme localmente mientras retiene su rigidez, mientras que un líquido cede al flujo viscoso macroscópico en respuesta a la aplicación de una fuerza de cizallamiento aplicada, es aceptado por muchos como la distinción mecánica entre los dos.[40][41]
Las deficiencias de esta conclusión, sin embargo, fueron señaladas por Frenkel en su revisión de la teoría cinética de los sólidos y la teoría de la elasticidad en los líquidos. Esta revisión se deriva directamente de la característica continua de la transición estructural del estado líquido al sólido cuando esta transición no está acompañada por la cristalización, por lo que se trata del líquido viscoso sobreenfriado. Así vemos la íntima correlación entre los fonones acústicos transversales (u ondas de corte) y el inicio de la rigidez en la vitrificación, como lo describe Bartenev en su descripción mecánica del proceso de vitrificación.[42][43]
Las velocidades de los fonones acústicos longitudinales en la materia condensada son directamente responsables de la conductividad térmica que nivela los diferenciales de temperatura entre los elementos de volumen comprimidos y expandidos. Kittel propuso que el comportamiento de los vidrios se interpreta en términos de una "trayectoria libre media" aproximadamente constante para los fonones, y que el valor de la trayectoria libre media es del orden de magnitud de la escala de desorden en la estructura molecular de un líquido o un sólido. El promedio térmico de las rutas libres o las longitudes de relajación de varios formadores de vidrio se han trazado en función de la temperatura de transición vítrea, lo que indica una relación lineal entre los dos. Esto ha sugerido un nuevo criterio para la formación de vidrio basado en el valor de la trayectoria libre media del fonón.[44]
A menudo se ha sugerido que el transporte de calor en sólidos dieléctricos se produce a través de las vibraciones elásticas de la red, y que este transporte está limitado por la dispersión elástica de los fonones acústicos por los defectos de la red (por ejemplo, vacantes espaciadas al azar).[45] Estas predicciones se confirmaron mediante experimentos en vidrios comerciales y vitrocerámicos, donde las rutas libres medias aparentemente estaban limitadas por la "dispersión del límite interno" a escalas de longitud de 10 a 100 micrómetros (0.00039-0.00394 pulgadas).[46][47] La relación entre estas ondas transversales y el mecanismo de vitrificación ha sido descrita por varios autores que propusieron que el inicio de las correlaciones entre dichos fonones da como resultado un ordenamiento o "congelación" de las tensiones de corte locales en los líquidos que forman vidrio, lo que produce la transición vítrea.[48]
Estructura electrónica
La influencia de los fonones térmicos y su interacción con la estructura electrónica es un tema que se introdujo adecuadamente en una discusión sobre la resistencia de los metales líquidos. Se hace referencia a la teoría de la fusión de Lindemann, y se sugiere que la caída de la conductividad al pasar del estado cristalino al líquido se debe a la mayor dispersión de los electrones de conducción como resultado de la mayor amplitud de la vibración atómica. Estas teorías de localización se han aplicado al transporte en vidrios metálicos, donde la trayectoria libre media de los electrones es muy pequeña (en el orden del espaciado interatómico).[49][50]
La formación de una forma no cristalina de una aleación de oro-silicio por el método de extinción de partículas a partir de la fusión llevó a consideraciones adicionales sobre la influencia de la estructura electrónica en la capacidad de formación de vidrio, basada en las propiedades del enlace metálico.[51][52][53][54][55]
Otro trabajo indica que la movilidad de los electrones localizados se ve aumentada por la presencia de modos de fonones dinámicos. Una observación contra tal modelo es que si los enlaces químicos son importantes, los modelos de electrones casi libres no deberían ser aplicables. Sin embargo, si el modelo incluye la acumulación de una distribución de carga entre todos los pares de átomos al igual que un enlace químico (por ejemplo, silicio, cuando una banda está llena de electrones), entonces debería aplicarse a los sólidos.[56]
Por lo tanto, si la conductividad eléctrica es baja, la trayectoria libre media de los electrones es muy corta. Los electrones solo serán sensibles al orden de corto alcance en el vidrio, ya que no tienen la oportunidad de dispersarse de los átomos espaciados a grandes distancias. Dado que el orden de corto alcance es similar en vidrios y cristales, las energías electrónicas deberían ser similares en estos dos estados. Para las aleaciones con menor resistividad y rutas electrónicas más largas y sin medios, los electrones podrían comenzar a sentir que hay un desorden en el vidrio, y esto elevaría sus energías y desestabilizaría el vidrio con respecto a la cristalización. Por lo tanto, las tendencias de formación de vidrio de ciertas aleaciones pueden deberse, en parte, al hecho de que las trayectorias libres del electrón son muy cortas, de modo que solo el orden de corto alcance es siempre importante para la energía de los electrones.
También se ha argumentado que la formación de vidrio en sistemas metálicos se relaciona con la "suavidad" del potencial de interacción entre átomos diferentes. Algunos autores, que enfatizan las fuertes similitudes entre la estructura local del vidrio y el cristal correspondiente, sugieren que el enlace químico ayuda a estabilizar la estructura amorfa.[57][58]
Otros autores han sugerido que la estructura electrónica cede su influencia en la formación del vidrio a través de las propiedades direccionales de los enlaces. La no cristalinidad se favorece así en elementos con un gran número de formas polimórficas y un alto grado de anisotropía de unión. La cristalización se vuelve más improbable a medida que aumenta la unión de la anisotropía del metal isotrópico al metal anisotrópico al enlace covalente, lo que sugiere una relación entre el número de grupo en la tabla periódica y la capacidad de formación de vidrio en sólidos elementales.[59]
Referencias
- ISO 11357-2: Plásticos @– calorimetría de barrido Diferencial @– Parte 2: Determinación de temperatura de transición del vaso (1999).
- «The Glass Transition». Polymer Science Learning Center. Archivado desde el original el 15 de enero de 2019. Consultado el 2 de diciembre de 2018.
- Debenedetti, P. G.; Stillinger (2001). «Supercooled liquids and the glass transition». Nature 410 (6825): 259-267. Bibcode:2001Natur.410..259D. PMID 11258381. doi:10.1038/35065704.
- Angell, C. A.; Ngai, K. L.; McKenna, G. B.; McMillan, P. F.; Martin, S. W. (2000). «Relaxation in glassforming liquids and amorphous solids». App. Phys. Rev. 88 (6): 3113-3157. Bibcode:2000JAP....88.3113A. doi:10.1063/1.1286035.
- Zarzycki, J. (1991). Glasses and the Vitreous State. Cambridge University Press. ISBN 978-0521355827.
- Ojovan, M. I. (2004). «Glass formation in amorphous SiO2 as a percolation phase transition in a system of network defects». Journal of Experimental and Theoretical Physics Letters 79 (12): 632-634. Bibcode:2004JETPL..79..632O. doi:10.1134/1.1790021.
- Meille Stefano, V.; Allegra, G.; Geil Phillip, H.; He, J.; Hess, M.; Jin, J.-I.; Kratochvíl, P.; Mormann, W.; Stepto, R. (2011). «Definitions of terms relating to crystalline polymers (IUPAC Recommendations 2011)». Pure Appl Chem 83 (10): 1831. doi:10.1351/PAC-REC-10-11-13.
- Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version(2006–) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. «IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book")».
- Hess, M.; Allegra, G.; He, J.; Horie, K.; Kim, J.-S.; Meille Stefano, V.; Metanomski, V.; Moad, G.; Stepto Robert, F. T.; Vert, M.; Vohlídal, J. (2013). «Glossary of terms relating to thermal and thermomechanical properties of polymers (IUPAC Recommendations 2013)». Pure Appl Chem 85 (5): 1017. doi:10.1351/PAC-REC-12-03-02.
- Hansen, J.-P.; McDonald, I. R. (2007). Theory of Simple Liquids. Elsevier. pp. 250-254. ISBN 978-0123705358.
- Adam, J-L; Zhang, X. (14 de febrero de 2014). Chalcogenide Glasses: Preparation, Properties and Applications. Elsevier Science. p. 94. ISBN 978-0-85709-356-1.
- Phillips, J.C. (1979). «Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys». Journal of Non-Crystalline Solids 34 (2): 153. Bibcode:1979JNCS...34..153P. doi:10.1016/0022-3093(79)90033-4.
- Moynihan, C. Et al. (1976) en La Transición de Vaso y la Naturaleza del Estado Vidrioso, M. Goldstein Y R. Simha (Eds.), Ann. N.Y. Acad. Sci., Vol. 279.
- Angell, C. A. (1988). «Perspective on the glass transition». Journal of Physics and Chemistry of Solids 49 (8): 863-871. Bibcode:1988JPCS...49..863A. doi:10.1016/0022-3697(88)90002-9.
- Ediger, M. D.; Angell, C. A.; Nagel, Sidney R. (1996). «Supercooled Liquids and Glasses». The Journal of Physical Chemistry 100 (31): 13200. doi:10.1021/jp953538d.
- Angell, C. A. (1995). «Formation of Glasses from Liquids and Biopolymers». Science 267 (5206): 1924-35. Bibcode:1995Sci...267.1924A. PMID 17770101. doi:10.1126/science.267.5206.1924.
- Stillinger, F. H. (1995). «A Topographic View of Supercooled Liquids and Glass Formation». Science 267 (5206): 1935-9. Bibcode:1995Sci...267.1935S. PMID 17770102. doi:10.1126/science.267.5206.1935.
- Thermodynamic and Kinetic Aspects of the Vitreous State. CRC Press. 1994. ISBN 978-0849337826.
- Gibbs, J. H. (1960). MacKenzie, J. D., ed. Modern Aspects of the Vitreous State. Butterworth. OCLC 1690554.
- Ojovan, Michael I; Lee, William (Bill) E (2010). «Connectivity and glass transition in disordered oxide systems». Journal of Non-Crystalline Solids 356 (44–49): 2534. Bibcode:2010JNCS..356.2534O. doi:10.1016/j.jnoncrysol.2010.05.012.
- Tg Medida de vasos. Glassproperties.com. Recuperado encima 2012-06-29.
- Vaso-temperatura de transición Archivado el 22 de diciembre de 2014 en Wayback Machine., IUPAC Compendium de Terminología Química, 66, 583 (1984)
- Galimberti, Maurizio; Caprio, Michela; Fino, Luigi (21 de diciembre de 2001). Tyre comprising a cycloolefin polymer, tread band and elasomeric composition used therein (publicado el 7 de marzo de 2003). «country-code =EU, patent-number =WO03053721 ».
- Ibeh, Christopher C. (2011). THERMOPLASTIC MATERIALS Properties, Manufacturing Methods, and Applications. CRC Press. pp. 491-497. ISBN 978-1-4200-9383-4.
- Wilkes, C. E. (2005). PVC Handbook. Hanser Verlag. ISBN 978-1-56990-379-7.
- ABS. nrri.umn.edu
- Nicholson, John W. (2011). The Chemistry of Polymers (4, Revised edición). Royal Society of Chemistry. p. 50. ISBN 9781849733915. Consultado el 10 de septiembre de 2013.
- nylon-6 información y propiedades. Polymerprocessing.com (2001-04-15). Recuperado encima 2012-06-29.
- Jones, A (2014). «Supplementary Materials for Artificial Muscles from Fishing Line and Sewing Thread». Science 343 (6173): 868-72. Bibcode:2014Sci...343..868H. PMID 24558156. doi:10.1126/science.1246906.
- Medida de Moisture Efectos en las Propiedades Mecánicas de 66 Nylon. TA Equipa #Escrito de Aplicación de Análisis Térmica TA-133
- PCL | Aplicaciones y Usos de Fin | Polythene. Polyesterconverters.com. Recuperado encima 2012-06-29.
- EPCOS 2007: Glass Transition and Crystallization in Phase Change Materials Archivado el 26 de julio de 2011 en Wayback Machine. . Retrieved on 2012-06-29.
- Bucaro, J. A. (1974). «High-temperature Brillouin scattering in fused quartz». Journal of Applied Physics 45 (12): 5324-5329. Bibcode:1974JAP....45.5324B. doi:10.1063/1.1663238.
- Kauzmann, Walter (1948). «The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures». Chemical Reviews 43 (2): 219-256. doi:10.1021/cr60135a002.
- Ojovan M.I. (2008). «Configurons: thermodynamic parameters and symmetry changes at glass transition». Entropy 10 (3): 334-364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334.
- Ojovan, M.I. (2008). «Configurons: thermodynamic parameters and symmetry changes at glass transition». Entropy 10 (3): 334-364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334.
- Ojovan, Michael I; Travis, Karl P; Hand, Russell J (2007). «Thermodynamic parameters of bonds in glassy materials from viscosity–temperature relationships». Journal of Physics: Condensed Matter 19 (41): 415107. Bibcode:2007JPCM...19O5107O. PMID 28192319. doi:10.1088/0953-8984/19/41/415107.
- Cowie, J. M. G. Y Arrighi, V., Polímeros: Química y Física de Materiales Modernos, 3.º Edn. (CRC Prensa, 2007)
- Slater, J.C., Introducción a Física Química (3.º Ed., Martindell Prensa, 2007)
- Born, Max (2008). «On the stability of crystal lattices. I». Mathematical Proceedings of the Cambridge Philosophical Society 36 (2): 160. Bibcode:1940PCPS...36..160B. doi:10.1017/S0305004100017138.
- Born, Max (1939). «Thermodynamics of Crystals and Melting». The Journal of Chemical Physics 7 (8): 591-603. Bibcode:1939JChPh...7..591B. doi:10.1063/1.1750497.
- Frenkel, J. (1946). Kinetic Theory of Liquids. Clarendon Press, Oxford.
- Bartenev, G. M., Estructura y Propiedades Mecánicas de Vasos Inorgánicos (Wolters @– Noordhoof, 1970)
- Reynolds, C. L. Jr. (1979). «Correlation between the low temperature phonon mean free path and glass transition temperature in amorphous solids». J. Non-Cryst. Solids 30 (3): 371. Bibcode:1979JNCS...30..371R. doi:10.1016/0022-3093(79)90174-1.
- Rosenburg, H. M. (1963) Temperatura Baja Física Estatal Sólida. Clarendon Prensa, Oxford.
- Kittel, C. (1946). «Ultrasonic Propagation in Liquids». J. Chem. Phys. 14 (10): 614. Bibcode:1946JChPh..14..614K. doi:10.1063/1.1724073.
- Kittel, C. (1949). «Interpretation of the Thermal Conductivity of Glasses». Phys. Rev. 75 (6): 972. Bibcode:1949PhRv...75..972K. doi:10.1103/PhysRev.75.972.
- Chen, Shao-Ping; Egami, T.; Vitek, V. (1985). «Orientational ordering of local shear stresses in liquids: A phase transition?». Journal of Non-Crystalline Solids 75 (1–3): 449. Bibcode:1985JNCS...75..449C. doi:10.1016/0022-3093(85)90256-X.
- Mott, N. F. (1934). «The Resistance of Liquid Metals». Proceedings of the Royal Society A 146 (857): 465. Bibcode:1934RSPSA.146..465M. doi:10.1098/rspa.1934.0166.
- Lindemann, C. (1911). «On the calculation of molecular natural frequencies». Phys. Z. 11: 609.
- Klement, W.; Willens, R. H.; Duwez, POL (1960). «Non-crystalline Structure in Solidified Gold–Silicon Alloys». Nature 187 (4740): 869. Bibcode:1960Natur.187..869K. doi:10.1038/187869b0.
- Duwez, Pol; Willens, R. H.; Klement, W. (1960). «Continuous Series of Metastable Solid Solutions in Silver-Copper Alloys». Journal of Applied Physics 31 (6): 1136. Bibcode:1960JAP....31.1136D. doi:10.1063/1.1735777.
- Duwez, Pol; Willens, R. H.; Klement, W. (1960). «Metastable Electron Compound in Ag-Ge Alloys». Journal of Applied Physics 31 (6): 1137. Bibcode:1960JAP....31.1137D. doi:10.1063/1.1735778.
- Chaudhari, P; Turnbull, D (1978). «Structure and properties of metallic glasses». Science 199 (4324): 11-21. Bibcode:1978Sci...199...11C. PMID 17841932. doi:10.1126/science.199.4324.11.
- Chen, J. S. (1980). «Glassy metals». Reports on Progress in Physics 43 (4): 353. Bibcode:1980RPPh...43..353C. doi:10.1088/0034-4885/43/4/001.
- Jonson, M.; Girvin, S. M. (1979). «Electron-Phonon Dynamics and Transport Anomalies in Random Metal Alloys». Phys. Rev. Lett. 43 (19): 1447. Bibcode:1979PhRvL..43.1447J. doi:10.1103/PhysRevLett.43.1447.
- Turnbull, D. (1974). «Amorphous Solid Formation and Interstitial Solution Behavior in Metallic Alloy System». J. Phys. C 35 (C4): C4–1. doi:10.1051/jphyscol:1974401.
- Chen, H. S.; Park, B. K. (1973). «Role of chemical bonding in metallic glasses». Acta Metall. 21 (4): 395. doi:10.1016/0001-6160(73)90196-X.
- Wang, R.; Merz, D. (1977). «Polymorphic bonding and thermal stability of elemental noncrystalline solids». Physica Status Solidi A 39 (2): 697. Bibcode:1977PSSAR..39..697W. doi:10.1002/pssa.2210390240.
Enlaces externos
- Fragilidad Archivado el 28 de junio de 2007 en Wayback Machine.
- VFT Eqn.
- Polímeros I
- Polímeros II Archivado el 11 de enero de 2010 en Wayback Machine.
- Angell: Medios de comunicación acuosos
- DoITPoMS Enseñanza y Aprendiendo Paquete- "La Transición de Vaso en Polímeros"