Tridente de Newton

El tridente de Newton es el nombre que se le da a una curva estudiada por Isaac Newton. También se le conoce como parábola de Descartes, aunque no es una parábola.[1]

Trident d'équation y = x²+1/x

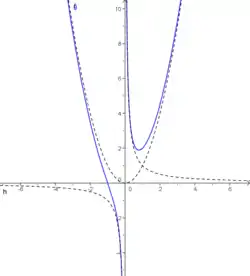
Clasificación de las cúbicas

En un estudio realizado en 1676 y publicado en 1704, Newton intentó clasificar todas las curvas cúbicas, es decir, todas aquellas curvas planas cuya ecuación es de la forma:

ax^{3}+bx^{2}y+cxy^{2}+dy^{3}+ex^{2}+fxy+gy^{2}+hx+iy+j=0\,

Newton contó 72 tipos, que pueden clasificarse en cuatro clases:

las curvas de ecuación $xy^{2}+ey=ax^{3}+bx^{2}+cx+d$
las curvas de ecuación $xy=ax^{3}+bx^{2}+cx+d$
las curvas de ecuación $y^{2}=ax^{3}+bx^{2}+cx+d$
las curvas de ecuación $y=ax^{3}+bx^{2}+cx+d$

Los llamados tridentes de Newton son del tipo 2.

Ecuación cartesiana

Los tridentes de Newton tienen por ecuación cartesiana canónica:

xy=ax^{3}+bx^{2}+cx+d\,

donde a y d no son nulos.

Análisis

Dominio

El dominio de los tridentes de Newton es:

D_{f}=\mathbb {R} ^{*}

Derivada

Como son funciones racionales $D_{f}$ , su derivada es:

f^{'}(x)=2ax+b-{\frac {d}{x^{2}}}

Límite en el infinito

En el infinito, los tridentes de Newton tienden a $+\infty$ , o bien a: $-\infty$ . Si a>0 entonces $\lim _{x\to \pm \infty }f(x)=+\infty$ . Si a<0 entonces $\lim _{x\to \pm \infty }f(x)=-\infty$ .

Límites en 0

En 0, los tridentes de Newton tienden a $+\infty$ o $-\infty$ .

Si d>0 entonces $\lim _{x\to 0^{+}}f(x)=+\infty$ y $\lim _{x\to 0^{-}}f(x)=-\infty$ .

Si d<0 entonces $\lim _{x\to 0^{+}}f(x)=-\infty$ y $\lim _{x\to 0^{-}}f(x)=+\infty$ .

Asíntotas

La asíntota de los tridentes de Newton es la parábola de ecuación:

y=ax^{2}+bx+c

También la hipérbola de ecuación:

y={\frac {d}{x}}

Intersección con el eje de las abscisas

Hay entre uno y tres puntos de intersección entre la curva del tridente de Newton y el eje horizontal de acuerdo con el valor de los coeficientes a, b, c, d.

Referencias

Eric W. Weisstein (2002). CRC Concise Encyclopedia of Mathematics. CRC Press. pp. 3045 de 3252. ISBN 9781420035223. Consultado el 26 de septiembre de 2023.

Enlaces externos

Portal:geometría . Contenido relacionado con geometría .

Datos: Q3539099
Multimedia: Trident curve / Q3539099

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[EWW-1] Eric W. Weisstein (2002). CRC Concise Encyclopedia of Mathematics. CRC Press. pp. 3045 de 3252. ISBN 9781420035223. Consultado el 26 de septiembre de 2023.