Cuerno de Gabriel

El cuerno de Gabriel (también llamado trompeta de Torricelli) es una figura geométrica que tiene la característica de poseer un área infinita pero un volumen finito. Es la superficie de revolución que se obtiene al girar, alrededor del eje X, el gráfico de la función F(x)=1/x, con dominio x ≥ 1.

Render POV-Ray del cuerno de Gabriel (su código fuente está en: )

Fue ideada por Evangelista Torricelli hacia 1641, que la bautizó como sólido hiperbólico agudo («solide hyperbolique aigu»).[1]

El nombre se refiere a la tradición abrahámica que identifica al arcángel Gabriel como el ángel que toca la bocina para anunciar el Día del Juicio

Paradoja aparente

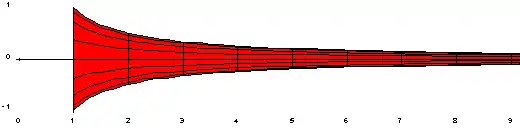
Imagen parcial del cuerno de Gabriel

En el momento de su descubrimiento, fue considerado una paradoja. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie exterior, mientras que sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.

La solución de la paradoja es que un área infinita requiere una cantidad infinita de pintura si la capa de pintura tiene un grosor constante. Esto no se cumple en el interior del cuerno, ya que la mayor parte de la longitud de la figura no es accesible a la pintura, especialmente cuando su diámetro es menor que el de una molécula de pintura. Si se considera una pintura sin grosor, sería necesaria una cantidad infinita de tiempo para que esta llegase hasta el «final» del cuerno.

En otras palabras, llegaría un momento en el que el espesor de la trompeta sería más pequeño que una molécula de pintura con lo que, digamos, una gota de pintura cubriría el resto de la superficie de la trompeta (aunque fuera infinito). Así, que la superficie de la trompeta sea infinita no implicaría que la cantidad de pintura tenga que ser infinita.

Pero la paradoja también tiene solución incluso si suponemos una materia divisible indefinidamente (o sea, si no existiesen los átomos). Si el grosor de la capa de pintura es variable y disminuye indefinidamente (tendiendo a cero), la cantidad de pintura se calcularía por una integral impropia que podría ser convergente. En este caso, el espesor de la capa de pintura forzosamente debería ser igual o menor al valor de y, lo que hace que la integral impropia, en este caso, sea convergente, es decir, se necesita una cantidad finita de pintura.

Es posible plantear otra forma de respuesta al pensar en la distancia numérica presente entre dos números consecutivos: Como bien sabemos, podemos obtener infinitos decimales si dividimos infinitas veces el espacio posible acotado entre esos dos números, lo cual no significa que la distancia entre ambos sea infinita.

Ecuación matemática

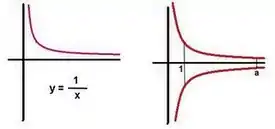
Gráfico de la función 1/x con dominio x≥1 girado en el eje X.

El cuerno de Gabriel se forma utilizando la gráfica de $y={\frac {1}{x}}$ , con el dominio $x\geq 1$ (al poseer la asíntota en $x=0$ ), y girándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo y fue posible gracias al principio de Cavalieri. Es posible calcular tanto el volumen $V$ como el área superficial $A$ del cuerno entre x = 1 y x = a, donde a > 1, mediante integración (véase sólido de revolución y superficie de revolución):

$V=\pi \int _{1}^{a}\left({1 \over x}\right)^{2}\,\mathrm {d} x=\pi \left(1-{1 \over a}\right)$

$A=2\pi \int _{1}^{a}{\frac {\sqrt {1+{\frac {1}{x^{4}}}}}{x}}\mathrm {d} x>2\pi \int _{1}^{a}{\frac {\sqrt {1}}{x}}\ \mathrm {d} x=2\pi \ln a.$

$a$ puede ser tan grande como se desee, pero en la ecuación se puede observar que el volumen del cuerno entre $x=1$ y $x=a$ nunca será igual a $\pi$ ; sin embargo, se acercará más y más a $\pi$ conforme $a$ crece. Matemáticamente, el volumen tiende a $\pi$ conforme $a$ tiende a infinito. Empleando límites, el volumen puede expresarse de la siguiente forma:

$\lim _{a\to \infty }V=\lim _{a\to \infty }\pi \left(1-{\frac {1}{a}}\right)=\pi \cdot \lim _{a\to \infty }\left(1-{\frac {1}{a}}\right)=\pi .$

Esto es así porque conforme $a$ tiende a infinito, $1/a$ tiende a cero, lo cual implica que el volumen tienda a $\pi$ (1 - 0), que es igual a $\pi$ .

Con respecto al área, la fórmula anterior muestra que esta es mayor que $2\pi$ veces el logaritmo neperiano de $a$ . No existe una cota superior para el logaritmo neperiano de $a$ conforme tiende a infinito, lo cual quiere decir que, en este límite, el cuerno tiene un área superficial infinita. Matemáticamente, esto es expresado de la siguiente forma:

$\lim _{a\to \infty }A\geq \lim _{a\to \infty }2\pi \ln(a)=\infty .$

Cuerno de Gabriel inverso

Lo contrario al cuerno de Gabriel, una superficie de revolución que tiene un área de superficie finita pero un volumen infinito, no puede ocurrir:

Teorema

Sea f : [1, ∞) → [0, ∞) ser una función continuamente diferenciable. Escriba S para el sólido de revolución de la gráfica y = f ( x ) sobre el eje x . Si el área de superficie de S es finita, entonces también lo es el volumen.

Prueba

Como el área de superficie lateral A es finita, el límite superior :

{\begin{aligned}\lim _{t\to \infty }\sup _{x\geq t}f(x)^{2}~-~f(1)^{2}&=\limsup _{t\to \infty }\int \limits _{1}^{t}\left(f(x)^{2}\right)'\mathrm {d} x\\&\leq \int \limits _{1}^{\infty }\left|\left(f(x)^{2}\right)'\right|\mathrm {d} x=\int \limits _{1}^{\infty }2f(x)\left|f'(x)\right|\mathrm {d} x\\&\leq \int \limits _{1}^{\infty }2f(x){\sqrt {1+f'(x)^{2}}}\mathrm {d} x={\frac {A}{\pi }}\\&<\infty .\end{aligned}}

Por lo tanto, existe un $t 0$ tal que el elemento supremo $sup{f (x) | x \geq t 0$ } es finito. Por lo tanto,

M = sup{f (x) | x \geq 1

} debe ser finito ya que

f

es una función continua, lo que implica que

f

está limitada en el intervalo

[1,\infty)

.

Finalmente, el volumen:

{\begin{aligned}V&=\int \limits _{1}^{\infty }f(x)\cdot \pi f(x)\mathrm {d} x\\&\leq \int \limits _{1}^{\infty }{\frac {M}{2}}\cdot 2\pi f(x)\mathrm {d} x\\&\leq {\frac {M}{2}}\cdot \int \limits _{1}^{\infty }2\pi f(x){\sqrt {1+f'(x)^{2}}}\mathrm {d} x={\frac {M}{2}}\cdot A.\end{aligned}}

Por lo tanto: si el área A es finita, entonces el volumen V también debe ser finito.

Véase también

Paradojas sobre el infinito

Notas

Encyclopédie ou Dictionnaire raisonné des sciences, des arts, et des métiers, Archivado el 3 de marzo de 2016 en Wayback Machine.

Enlaces externos

Weisstein, Eric W. «Gabriel's Horn». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Información y diagramas sobre el cuerno de Gabriel (en inglés)

Datos: Q723694
Multimedia: Gabriel's horn / Q723694

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Encyclopédie ou Dictionnaire raisonné des sciences, des arts, et des métiers, Archivado el 3 de marzo de 2016 en Wayback Machine.