États limites ultime et en service

Les pièces — éléments de mécanismes ou de structures — sont soumises à des sollicitations : efforts extérieurs, vibrations, dilatation… Elles sont en général dimensionnées selon deux critères :

l'état limite ultime, ou ELU (en anglais, ultimate limit state, ULS), qui consiste à vérifier qu'elles ne subissent pas de déformation irréversible sous la charge, et a fortiori qu'elles ne présentent pas de dégradation ;
l'état limite en service, ou ELS (serviceability limit state, SLS), qui consiste à vérifier que leur déformation élastique reste compatible avec le fonctionnement.

Déformations élastique et plastique

Considérons une pièce faite d'un matériau ductile. Lorsque l'on augmente progressivement la charge, la pièce passe par trois étapes successives :

la déformation élastique : c’est la déformation non permanente que subit un matériau sous un certain chargement; la pièce reprend sa forme initiale dès que cesse cette contrainte ;
la déformation plastique, permanente : le matériau a atteint la limite d'élasticité et la pièce ne reprend pas sa forme initiale ;
la dégradation, prélude de la rupture.

Si la pièce est faite d'un matériau fragile, comme un verre, une céramique, un béton, un acier trempé, une fonte non ductile, … alors elle reste dans le domaine élastique jusqu'à la rupture. Dans ce cas, la validation à l'ELU est un critère de résistance à la rupture.

Cas des sollicitations simples

Pour un même matériau, cette résistance à la déformation dépend du type de sollicitation ou de fatigue qu’il subit. Nous nous référons ici à la théorie des poutres.

Traction ou extension

Les câbles de cette grue sont soumis à de la traction.

Lorsqu’une pièce est sollicitée à l’extension par une force F, on calcule sa contrainte normale σ (lettre grecque « sigma ») :

\sigma ={\frac {\mathrm {F} }{\mathrm {S} }}

La validation à l'ELU consiste à vérifier que cette contrainte est inférieure ou au plus égale à la résistance pratique à l’extension R_pe :

σ ≤ R_pe

La résistance pratique à l'extension est définie :

dans le cas d'un matériau ductile, à partir de la limite d'élasticité : R_pe = R_e/s ;
dans le cas d'un matériau fragile, à partir de la résistance à la traction : R_pe = R_m/s.

où s est le coefficient de sécurité.

Sous l'effet de la traction, la pièce, de longueur initiale l₀ s'allonge qu'une quantité ΔL vérifiant la loi de Hooke :

σ = E×ε avec ε = ΔL/L₀

où E est le module de Young du matériau, et ε est l'allongement relatif. La vérification à l'ELS consiste à vérifier que la longueur finale

\mathrm {L} =\mathrm {L} _{0}+\Delta \mathrm {L} =\mathrm {L} _{0}(1+\varepsilon )=\mathrm {L} _{0}\left(1+{\frac {\sigma }{\mathrm {E} }}\right)

est compatible avec le fonctionnement.

Par ailleurs, sa dimension transverse a₀ (largeur, épaisseur, rayon) diminue d'une quantité Δa vérifiant :

{\frac {\Delta a}{a_{0}}}=-\nu \varepsilon =-\nu {\frac {\Delta \mathrm {L} }{\mathrm {L} _{0}}}

.

Cet amincissement augmente le jeu et peut provoquer un desserrage si la pièce est sertie. La validation à l'ELS consiste donc également à vérifier que l'ajustement final est fonctionnel.

Compression

Un pylone travaille essentiellement en compression.

Comme pour l’extension, une pièce courte comprimée doit avoir une contrainte de compression inférieure à la résistance pratique à la compression du matériau.

σ ≤ R_pc

avec R_pc = R_ec/s ou R_mc/s. Pour un certain nombre de matériaux isotropes, les limites d'élasticité en traction et en compression sont égales :

R_ec = R_e

R_mc = R_m

Ce n'est pas le cas pour les bétons et les fontes.

La déformation se fait comme pour la traction ; la longueur diminue d'une quantité ΔL tandis que la dimension transverse augment d'une quantité Δa, selon les mêmes équations que précédemment (seules changent les signes des grandeurs). La validation à l'ELS consiste à vérifier que ces variations ne nuisent pas à la fonction de la pièce.

Flambement

La charge critique de flambage, ou flambement, F est la charge pour laquelle la pièce présente un risque d'instabilité en compression : au lieu de simplement se raccourcir et de s'élargir, elle peut se courber. L'expression de cette charge critique est donnée par la formule d'Euler :

\mathrm {F} ={\frac {\pi ^{2}\mathrm {E} \mathrm {I} }{l_{\mathrm {k} }^{2}}}

où

E est le module de Young du matériau ;
I est le moment quadratique de la poutre ;
l_k est la longueur de flambement de la poutre, ou élancement.

Si le flambage est évité, la pièce est simplement en compression. La validation à l'ELS est donc celui de la compression.

Flexion

Lame de scie déformée en flexion.

Dans une pièce soumise à de la flexion, la matière est soumise à de la traction/compression. La contrainte normale maximale vaut

\sigma _{\max }={\frac {\mathrm {M_{f\ max}} }{\mathrm {W_{{\acute {e}}l}} }}

avec :

M_{f max} : moment de flexion maximal (N m) ;
W_él : module de flexion de la section du matériau (m³).

Le module de flexion est calculé à partir du moment quadratique autour de l'axe de flexion, par exemple I_Gz, et la distance maximale par rapport à la fibre neutre selon l'axe perpendiculaire, V_y :

\mathrm {W} _{\mathrm {{\acute {e}}l} .z}={\frac {\mathrm {I} _{\mathrm {G} z}}{v_{y}}}

La validation à l'ELU consiste à vérifier que

σ_max ≤ R_pe

Sous la charge, la pièce se déforme transversalement. Il faut donc évaluer le débattement maximal, appelé « flèche » ƒ. Dans les cas simples, l'évaluation de la flèche peut se faire à partir de formulaires (voir par exemple Wikibooks : Formulaire des poutres simples - Déformée), ou bien par un calcul intégral.

La validation à l'ELS consiste à vérifier que la flèche ne dépasse pas une valeur donnée. Dans le cas d'un axe, la flèche doit être inférieure au jeu pour ne pas provoquer de serrage. En génie civil, la flèche admissible dépend de la longueur L de la poutre, par exemple elle vaut :

L/150 (soit 1/150 de la portée L) pour les parties d'ouvrage en console n'ayant pas à supporter couramment une circulation (auvents, débords de toiture), pour les tubes d'une structure supportant un poste électrique HTB (norme de l'entreprise publique française RTE) ;
L/200 pour les pièces supportant directement des éléments de couverture (chevrons, liteaux), la charpente d'une structure supportant un poste électrique HTB (RTE)
L/250 pour une poutre, dalle ou console soumise à des charges quasi permanentes (clause 7.4.1.4 de l'Eurocode 2. Béton armé) ;
L/300 pour une solive supportant un plancher, les pannes, les pièces supportant directement des matériaux verriers, les consoles supportant une circulation (montage ou entretien), les poteaux avec ponts roulants, les poteaux avec remplissage en maçonnerie prenant appui sur le poteau, les poteaux destinés à recevoir un vitrage sur plus de la moitié de leur hauteur, les éléments fléchis reposant sur deux ou plusieurs appuis, et ne supportant pas d'éléments de remplissage ;
L/400 pour les ouvrages fléchis autres que les consoles, et supportant une circulation (montage ou entretien) ou un remplissage ;
L/500 pour un linteau de menuiserie ;
L/600 pour un pont forestier neuf acier-bois (Ministère des ressources naturelles, Québec) ;
…

Lorsque la poutre subit une déformation irréversible et que par conséquent la matière entre dans le domaine plastique, on fait appel à la notion de rotule plastique afin de déterminer le comportement de la structure.

Cisaillement simple

Rupture d'un axe en porte-à-faux ou en chape.

Le cisaillement simple est une situation où deux forces opposées s'appliquent en étant légèrement décalées. La contrainte de cisaillement, ou cission, est notée τ (lettre grecque « tau ») et vaut

\tau ={\frac {\mathrm {F} }{\mathrm {S} }}

où

F est l'effort tranchant, en newtons (N) ;
S est l'aire de la section cisaillée, en millimètres carrés (mm²).

Il importe de dénombrer les sections cisaillées : dans le cas d'un axe en porte-à-faux, il n'y a qu'une seule section cisaillée, S est donc l'aire de la section droite. Mais pour un axe en chape, l'effort se répartit sur plusieurs tronçons, il y a au total deux sections cisaillées, donc S vaut deux fois l'aire de la section droite.

La validation à l'ELU consiste à vérifier que

τ ≤ R_pg

La résistance pratique au glissement, R_pg, est définie à partir de la résistance élastique au glissement R_eg :

R_pg = R_eg/s.

Pour les métaux, la résistance élastique au glissement est reliée à la limite d'élasticité :

0,5×R_e ≤ R_eg ≤ 0,8×R_e.

Déformation dans le cas d'un cisaillement simple

Sous l'effet du couple de forces, la poutre subit localement une déviation. L'angle de déviation, γ (lettre grecque « gamma »), est relié à la contrainte par le module de cisaillement G du matériau :

τ = G×γ

où τ et G sont en mégapascals et γ est en radians. Les deux tronçons de la pièce se décalent d'une valeur v valant :

v = Δx×tan γ ≈ Δx×γ.

la valeur Δx étant l'écartement entre les points d'application des forces.

La validation à l'ELS consiste à vérifier que cette déformation est compatible avec la fonction de la pièce.

Torsion

Dans une pièce soumise à de la torsion, la matière se déforme en cisaillement. La contrainte de cisaillement maximale, ou cission maximale, vaut :

\tau _{\max }={\frac {\mathrm {M_{t}} }{\mathrm {C} }}

avec

M_t : le moment de torsion (mm N) ;

C : module de torsion de la section du matériau (mm³).

Dans le cas d'une poutre de section fermée circulaire, le module de torison se calcule à partir du moment quadratique I_G et du rayon v :

\mathrm {C} ={\frac {\mathrm {I_{G}} }{v}}

.

La validation à l'ELU consiste à vérifier que l'on ne dépasse pas la résistance pratique au glissement R_pg

τ_max ≤ R_pg.

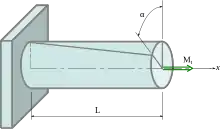
Rotation des sections sous l'effet du moment de torsion.

La torsion crée la rotation d'une extrémité par rapport à l'autre extrémité autour de l'axe. L'angle de rotation relatif est noté α (lettre grecque « alpha »). Pour un moment M_t donné, plus la pièce est longue, plus α est important. On définit un angle de torsion unitaire θ (lettre grecque « thêta ») en radians par millimètre (rad/mm), qui vérifie l'équation

M_t = G×θ×I_G

où G est le module de cisaillement du matériau. L'angle total de rotation vaut

α = L×θ

où L est la longueur de la pièce, soit

\alpha ={\frac {\mathrm {L} \mathrm {M_{t}} }{\mathrm {G} \mathrm {I_{G}} }}

La validation à l'ELS consiste à vérifier que cette rotation est compatible avec le fonctionnement de l'ensemble.

Cas des sollicitations composées

Flexion + torsion

Lorsqu’un arbre de transmission subit à la fois une torsion et une flexion, sa matière subit à la fois de la contrainte normale et de la contrainte de cisaillement.

On définit un moment de flexion idéal M, qui est le moment générant un risque de rupture équivalent au moment de flexion réel M_f et au moment de torsion M_t :

\mathrm {M} =0,35\mathrm {M_{f}} +0,65{\sqrt {\mathrm {M_{f}} ^{2}+\mathrm {M_{t}} ^{2}}}

Puis on calcule une contrainte normale équivalente comme en flexion :

\sigma _{\mathrm {eqv} }={\frac {\mathrm {M} }{\mathrm {W_{{\acute {e}}l}} }}

La validation à l'ELU consiste à vérifier que

σ_eqv ≤ R_pe.

Cette méthode n'est valable que pour les pièces de section cylindrique fermée.

La validation à l'ELS consiste à déterminer séparément les déformations à la flexion et à la torsion (principe de superposition pour les petites déformations).

Flexion + extension ou compression

La flexion et l'extension/compression créent de la contrainte normale. On peut donc calculer la contrainte maximale comme étant la somme

de la contrainte normale due à la traction/compression, σ_N = F/S, et
de la contrainte maximale de flexion, σ_f = M_{f max}/W_él

σ_max = σ_N + σ_f

et la validation à l'ELU consiste à vérifier que

σ_max ≤ R_pe.

La validation à l'ELS consiste à appliquer indépendamment la déformation en traction-compression et en flexion.

Torsion + cisaillement

La torsion comme le cisaillement simple créent de la contrainte de cisaillement τ. La contrainte résultante est simplement la somme des deux contraintes calculées indépendamment :

τ_c = F/S

τ_t = M_t/C

τ = τ_c + τ_t

La validation à l'ELU consiste à vérifier que

τ ≤ R_pg.

Voir aussi

Bibliographie

Normes

Eurocode 2
Eurocode 3
Codap
Codeti
Règles de calcul et de conception des charpentes en bois : règles C.B 71 (norme P21-701), Afnor
EC5

Articles connexes

Portail des sciences des matériaux
Portail de la physique
Portail du génie mécanique
Portail du bâtiment et des travaux publics

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.