Œnopide de Chios
Œnopide de Chios (milieu du Ve siècle av. J.-C.) était un mathématicien et astronome grec.
| Naissance | |
|---|---|
| Décès |
Vers |
| Activités | |
| Période d'activité |
Ve siècle av. J.-C. |
Contributions
Ses travaux concernent Le mouvement propre du Soleil et L’obliquité de l’Écliptique.
D’après Eudème de Rhodes, lui-même cité par Théon de Smyrne (par l'intermédiaire de Dercyllides (en)) :
« Eudème dans ses livres Sur l’astronomie raconte qu’Œnopide a trouvé le premier l’obliquité du zodiaque et reconnu l’existence de la grande année : d’après lui, Thalès a fait voir que les éclipses de soleil et les retours de cet astre aux solstices n’arrivent pas toujours après le même temps ; Anaximandre prétend que la terre est suspendue dans l’espace et se meut autour du centre du monde ; Anaximène a montré que la lune reçoit la lumière du soleil et de quelle manière elle s’éclipse. D’autres ont ajouté de nouvelles découvertes à celles-là : que les étoiles se meuvent autour de l’axe immobile qui passe par les pôles, que les planètes se meuvent autour de l’axe perpendiculaire au zodiaque ; et que l’axe des étoiles et celui des planètes s’écartent l’un de l’autre, du côté du pentédécagone, et par conséquent d’un angle de 24 degrés. »
— Des connaissances mathématiques utiles pour la lecture de Platon, L.III, XL.
Il fixe l' obliquité de l'écliptique à 24°, valeur qui sera conservée pendant plusieurs siècles dans l'Antiquité[1] ; on lui attribue la construction de la médiatrice d'un segment comme droite joignant les points d'intersection de deux cercles de même rayon centrés sur les extrémités de ce segment.
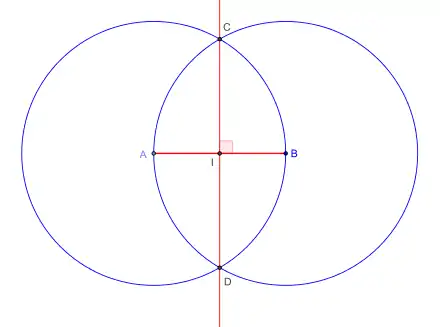

Eudème, cité par Proclus, attribuait à Œnopide de Chios, la découverte du problème relatif à la proposition 23 du livre I d'Euclide : « Sur une droite donnée, et en un point donné sur cette droite, construire un angle égal à un angle donné. »[2].
Pour reporter l'angle de O en I, avec la règle et le compas, tracer deux cercles de même rayon centrés en O et I, tracer les points A et B intersection des côtés de l'angle avec le cercle de centre O, choisir un point C sur le cercle de centre I, et reporter la longueur AB en traçant un troisième cercle de centre C qui coupe le deuxième cercle en D (et en un autre point).
L'angle est égal à l'angle .
Notes et références
- A. Szabo - E. Maula (trad. de l'allemand), Les débuts de l'astronomie, de la géographie et de la trigonométrie chez les Grecs, Paris, J. Vrin, coll. « L'histoire des sciences, textes et études », , 238 p. (ISBN 2-7116-0911-1), p. 164-165.
- Histoire des mathématiques, Colette, 1973.
Voir aussi
Bibliographie
- (en) István M. Bodnár, « Oenopides of Chius: A survey of the modern literature with a collection of the ancient testimonia », sur Institut Max-Planck d'histoire des sciences, , preprint 327
- Johann Philipp Heinius, « Dissertation sur Oenopidas de Chio », Histoire de l'Académie royale des sciences et des belles-lettres de Berlin, , p. 401-424 (lire en ligne)
- Jean-Yves Strasser, « La fête des Daidala de Platées et la « Grande année » d'Oinopidès », Hermès, Revue de Philologie, vol. 132, no 3, , p. 338-351 (lire en ligne)
Articles connexes
Liens externes
- Ressource relative à l'astronomie :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Portail de la géométrie
- Portail des mathématiques