Surface spécifique

La surface spécifique désigne le rapport de la superficie de la surface réelle d'un objet (par opposition à sa surface apparente) et de la quantité de matière de l'objet (en général sa masse, parfois son volume apparent). On l'exprime donc généralement comme une aire massique, en unités de surface par unité de masse : en mètres carrés par kilogramme (m2/kg), l'unité SI, ou en mètres carrés par gramme (1 m2/g = 1 000 m2/kg). Quand la surface spécifique est rapportée au volume (aire volumique), on l'exprime en unités de surface par unité de volume, par exemple en mètres carrés par mètre cube, l'unité SI, c'est-à-dire en m−1 (= m2/m3).

Pour les articles homonymes, voir Surface.

La surface spécifique a une grande importance pour les phénomènes faisant intervenir les surfaces (adsorption, absorption, catalyse, échanges de chaleur). Elle est surtout intéressante pour les matériaux divisés (poudres, mousses, pailles métalliques), car c'est seulement pour ce type de matériaux qu'elle ne dépend pas de la masse de l'objet considéré, à l'instar des autres grandeurs spécifiques.

Illustration
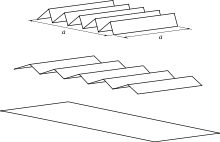
À surface apparente égale, la présence de rayures (symbolisées ici par des sillons triangulaires) augmente la surface spécifique.

Prenons un cube d'arête a présentant des rayures régulières, les rayures ayant un profil triangulaire. La surface apparente Sapp du cube est la somme des aires de ses six faces : Sapp = 6 a2. Mais regardons une face de près : chaque rayure est un sillon, il faut prendre en compte l'aire des flancs de chaque sillon. Si l'on « déplie » la surface, on voit que l'on obtient une aire plus grande que la surface apparente ; la surface réelle est supérieure à la surface apparente (elles ne sont égales que si la surface est strictement plane et lisse) : Sréelle ≥ Sapp. La surface spécifique d'un tel cube sera donc supérieure à celle d'un cube lisse.

Surface spécifique et porosité

Un pore est une cavité dans un objet. On distingue deux sortes de pores : les pores fermés, qui ne communiquent pas avec l'extérieur, et les pores ouverts qui sont reliés à l'extérieur, soit directement, soit via d'autres pores et un réseau de canaux ou de fissures. Les fluides peuvent diffuser dans les pores ouverts, qui participent ainsi à la surface réelle (et donc à la surface spécifique).

Surface spécifique et granulométrie

Dans le cas d'une poudre ou d'un sol, la surface réelle est la somme des surfaces des grains. La surface spécifique est alors la surface totale des particules individuelles divisée par la masse de matériau considérée. En général on ne prend en compte que la masse sèche (la surface spécifique ne dépend alors pas de l'hygrométrie).

D'une manière générale, plus les grains sont fins, plus la surface spécifique est importante. Par exemple, pour des grains sphériques de rayon r et de masse volumique ρ :

.
Démonstration

Supposons que les grains soient sphériques et aient tous le même rayon r ; ils ont tous la même masse volumique ρ (parfois appelé « densité théorique », puisque c'est la densité de la matière sous forme massive). Le volume d'un grain est v = 4/3·π·r3 et la masse d'un grain est m = ρ·v = ρ·4/3·π·r3.

Sa surface est s = 4·π·r2.

Donc, si l'on considère n grains, ils représentent une masse M = n·m = n·ρ·4/3·π·r3 et la surface réelle est Sréelle = n·s = n·4·π·r2.

On peut donc relier la surface réelle à la masse totale et au rayon Sréelle = 3·M/(ρ·r) ; on a donc pour la surface spécifique Sspé = 3/(ρ·r).

On voit que pour une quantité de matière donnée, la surface spécifique est inversement proportionnelle au rayon des grains de poudre.

Ce modèle est simpliste puisque les grains sont en général ni sphériques, ni de même taille, et que de plus ils peuvent être agglomérés (ce qui diminue la surface libre).

Le tableau ci-dessous donne des valeurs de surface spécifique pour quelques matériaux utilisés pour leurs propriétés de surface (catalyseur hétérogène, absorbeur) en appliquant la formule ci-dessus. Cela permet de fixer un ordre de grandeur.

Exemple de calculs de surface spécifique
Matériau
(masse volumique théorique)		 Rayon
1 mm 100 µm 10 µm 1 µm 100 nm 10 nm 1 nm
Platine
(21 450 kg m−3)		 0,14 m2 kg−1 1,4 m2 kg−1 14 m2 kg−1 140 m2 kg−1
0,14 m2 g−1		 1 400 m2 kg−1
1,4 m2 g−1		 14 m2 g−1 140 m2 g−1
Nickel
(8 908 kg m−3)		 0,34 m2 kg−1 3,4 m2 kg−1 34 m2 kg−1 340 m2 kg−1
0,34 m2 g−1		 3 400 m2 kg−1
3,4 m2 g−1		 34 m2 g−1 340 m2 g−1
Graphite
(2 250 kg m−3)		 1,3 m2 kg−1 13 m2 kg−1 130 m2 kg−1
0,13 m2 g−1		 1 300 m2 kg−1
1,3 m2 g−1		 13 m2 g−1 130 m2 g−1 1 300 m2 g−1

Le lien avec le volume total est plus complexe. En effet, celui-ci dépend de l'organisation de la poudre. La poudre a une masse volumique apparente ρapp qui est le rapport entre la masse et le volume extérieur V occupé par la poudre (le volume du contenant que l'on a rempli de poudre) : ρapp = M/V soit V = M/ρapp ; on a donc Sréel = 3·(V/r )·(ρapp/ρ).

Le rapport de la densité apparente sur la densité théorique est en fait la densité volumique d, c'est-à-dire la fraction de l'espace occupée par les grains : Sréelle = 3·d·V/r soit, si l'on exprime la surface spécifique en aire par unité de volume : Sspé = 3·d/r.

empilement compact de 35 sphères

Si l'on estime que les grains sont indéformables, alors dans le cas d'une poudre très tassée, on a une compacité maximale. On peut donc la décrire par le modèle de l'empilement compact. On a alors une densité volumique d = π/(3·√2) ≅ 0,74.

Donc dans le cas d'un empilement compact, d étant fixé, on voit que pour un volume donné, la surface réelle est également inversement proportionnelle au rayon des grains. Ceci est faux dans le cas absolu, puisqu'il est difficile de prévoir l'organisation de la poudre.

La surface par unité de volume est indépendante de la masse volumique du matériau. Quelques valeurs sont indiquées ci-dessous.

Exemple de calculs de surface spécifique dans le cas d'un empilement compact
Rayon 1 mm 100 µm 10 µm 1 µm 100 nm
Sspé 2 220 m2 m−3
0,002 m2 cm−3		 2,22 × 104 m2 m−3
0,02 m2 cm−3		 2,22 × 105 m2 m−3
0,22 m2 cm−3		 2,22 × 106 m2 m−3
2,22 m2 cm−3		 2,22 × 107 m2 m−3
22,2 m2 cm−3

Détermination

La surface spécifique peut être déterminée par la mesure[1] :

  • de l'adsorption d'un gaz sur la surface d'un matériau de masse ou de volume connu à une température donnée et dans un certain domaine de pression relative. La courbe obtenue est appelée isotherme d'adsorption. La technique la plus utilisée est celle basée sur la théorie Brunauer, Emmett et Teller (BET). Avec cette technique, il faut mesurer la quantité de diazote nécessaire pour avoir une mono-couche de ce gaz sur la surface[2].
  • de la perméabilité à un gaz d'un milieu poreux ou d'un lit de poudre constitué de particules non microscopiques[3].

Exemples et applications

Échanges de chaleur
Radiateurs (échangeurs de chaleur à ailettes) utilisés pour évacuer la chaleur de microprocesseurs d'ordinateur
Lampe de Davy
Échangeur de chaleur à tubes rectilignes

Pour réduire leur perte de chaleur, les manchots de l'Antarctique se regroupent en « tortue » : ils réduisent ainsi la surface corporelle exposée au froid. Dans le même ordre d'idées, l'Homme se recroqueville en position fœtale. La stratégie consiste à réduire la surface spécifique.

À l'inverse, si l'on veut augmenter l'échange de chaleur, on augmente la surface de contact :

  • les radiateurs (utilisés pour évacuer la chaleur d'un milieu ou pour chauffer un milieu) ont des formes relativement complexes pour avoir une grande surface d'échange avec l'air :
    • les radiateurs de microprocesseurs sont souvent sous la forme de lames ;
    • les radiateurs de moteurs de voiture comportent souvent une grille métallique ;
    • les radiateurs de chauffage d'une habitation ne sont que rarement plats mais possèdent au contraire des reliefs ;
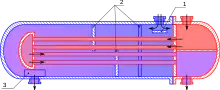
  • les échangeurs de chaleur sont souvent sous la forme d'un tuyau transportant un fluide (liquide ou gaz) et baignant dans un récipient contenant un autre fluide ; la grande longueur de tuyau offre une grande surface d'échange :
  • pour éviter la propagation d'une flamme dans une atmosphère explosive, on protège souvent un appareil produisant de la chaleur ou des étincelles par une fine grille ; ainsi, si une flamme s'amorce, lorsqu'elle atteint la grille, la chaleur qu'elle produit se dissipe dans le métal de la grille et la réaction explosive ne peut se propager à l'extérieur ; c'est notamment le principe de la lampe de Davy, utilisée pour éviter les coups de grisou.

Absorption et contact entre les réactants
Villosités intestinales


Grille de platine
Mousse pour lutter contre les feux d'hydrocarbure

Une éponge possède une grande surface spécifique (beaucoup de porosité). Elle peut ainsi absorber beaucoup d'eau. Une pierre ponce a également une grande porosité, l'air piégé dans ses pores permet de diminuer sa masse volumique apparente.

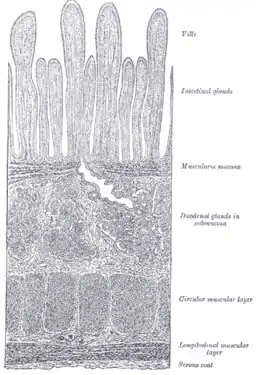
L'intestin grêle possède également une très grande surface spécifique, grâce à ses villosités : environ 250 m2 pour une longueur de 7 m et un diamètre de 4 cm, soit à peu près 2,8 × 104 m−1. Il y a donc une très grande surface de contact avec le bol alimentaire (chyme) ce qui permet aux nutriments de passer facilement dans le sang.

Dans le cas de la catalyse hétérogène, la réaction chimique a lieu à la surface du catalyseur. On cherche donc à avoir la plus grande surface pour une quantité de matière la plus faible, afin de réduire le volume et les coûts (certains matériaux, comme le platine ou le palladium, étant prohibitifs) : grille, poudre, mousse, zéolithe…

  • le charbon activé a une surface spécifique comprise entre 400 et 2 500 m2 g−1, soit de 4 × 105 à 2,5 × 106 m2 kg−1, essentiellement due à sa porosité ;
  • le nickel de Raney disponible commercialement possède une surface spécifique moyenne de l'ordre de 100 m2 g−1, soit 105 m2 kg−1.

Lorsqu'un matériaux présente une grande surface spécifique, il devient donc très réactif. C'est ainsi que l'oxydation d'un métal, habituellement peu dangereuse (la rouille du fer par exemple), peut devenir explosive si celui-ci est réduit en fine poudre (voir Métallurgie des poudres). Ce phénomène intervient également dans les coups de poussière et les explosions de silo agricoles. Lorsque l'on veut faire des réactions entre solides, on les réduits en poudre et on les mélange (voir par exemple l'aluminothermie ou le frittage réactif).

Exemple : pour éteindre les feux notamment d'hydrocarbure (essence, pétrole…), les pompiers recouvrent la nappe enflammée d'une mousse : on crée ainsi une grande surface isolante avec une quantité réduite d'eau et d'émulsifiant, et surtout avec une masse volumique faible qui lui permet de flotter sur l'hydrocarbure. On parle de foisonnement (mousse à haut ou à bas foisonnement). Le mélange eau et émulsifiant forme des bulles, donc une mince pellicule avec une très grande surface spécifique comparé à une « flaque ».

Autres exemples

Dans le cas d'un brûleur, la combustion a lieu dans une fine zone appelée front de flamme. Pour avoir la plus grande puissance de chauffe dans un espace réduit, il faut donc avoir la plus grande surface de front de flamme dans ce volume, ce qui s'obtient en pulvérisant finement le combustible.

À titre de comparaison
  • Une boule de pétanque de 8 cm de diamètre et de 800 g supposée parfaitement lisse a une surface spécifique de 2,5 × 10−5 m2 g−1, soit 0,025 m2 kg−1, ou encore 37,5 m−1 ;
  • un adulte a environ 1,5 à 2 m2 de peau ; en considérant une masse corporelle de 70 kg, cela représente une surface spécifique de 2 à 3 × 10−5 m2 g−1, soit de 0,02 à 0,03 m2 kg−1, ou, la densité du corps étant voisine de 1[4], une valeur de 20 à 30 m−1.

Notes et références
  1. Henri Fauduet, Mécanique des fluides et des solides appliquée à la chimie, Lavoisier, 2011
  2. ISO 9277:2010 Septembre 2010 Détermination de l'aire massique (surface spécifique) des solides par adsorption de gaz - Méthode BET
  3. ISO 10070:1991 Décembre 1991 Poudres métalliques. Détermination de la surface spécifique d'enveloppe à partir de mesures de la perméabilité à l'air d'un lit de poudre dans des conditions d'écoulement permanent

Voir aussi

Articles connexes
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.