Algorithme évolutionniste

Tous les algorithmes évolutionnaires font évoluer un ensemble (une « population ») de solutions (les « individus »). Les individus sont représentés par leur génotype, qui s'exprime sous la forme d'un phénotype, auxquels on associe une qualité, la « fitness ». Les algorithmes sont conçus de façon que plus la fitness d'un individu est élevée, plus il a de chances de transmettre son génotype au sein de la population.

À chaque étape de l'algorithme est associé un « opérateur », qui décrit la façon de manipuler les individus. On regroupe parfois les différents opérateurs sous des termes génériques :

• opérateurs de sélection pour la sélection et le remplacement,
• opérateurs de variation pour la mutation et le croisement.

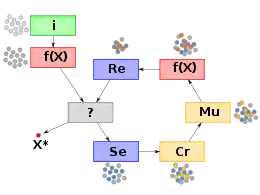
Pour ce faire, on utilise l'algorithme général suivant :

construction et évaluation d'une population initiale ;
Jusqu'à atteindre un critère d'arrêt :
  sélection d'une partie de la population,
  reproduction des individus sélectionnés,
  mutation de la descendance,
  évaluation du degré d'adaptation de chaque individu,
  remplacement de la population initiale par une nouvelle population.

Après avoir initialisé une première population d'individus, on itère un nombre fini de fois, jusqu'à atteindre un critère d'arrêt (par exemple un nombre maximum de générations). La première étape de sélection permet de séparer les individus qui participeront à la reproduction de ceux qui n'y participeront pas. Les individus sélectionnés (les « parents ») se reproduisent (on dit aussi que l'on effectue des croisements), donnant un ensemble d'« enfants » partageant une partie des caractéristiques de leurs ascendants. Ces enfants subissent alors une étape de mutation, qui modifie aléatoirement leur génotype. Les nouveaux individus sont alors évalués (on met à jour leur valeur en faisant appel à la fonction objectif). Enfin, on choisit un nombre d'individus déterminé parmi l'ensemble parents + enfants, pour former la génération suivante.

Les notions d'intensification (ou exploitation), de diversification (ou exploration) et de processus aléatoires sont au cœur du comportement des opérateurs utilisés par les algorithmes évolutionnaires.

Il existe toujours au moins un opérateur utilisant un processus aléatoire, au minimum pour la construction de la population initiale et pour la mutation, mais souvent pour la sélection et la reproduction également. Selon les méthodes, on met l'accent sur l'un ou l'autre des opérateurs.

Une pratique courante reste de maintenir suffisamment longtemps la « diversité génétique » de la population, afin d'éviter une convergence prématurée. Quand un algorithme évolutionnaire utilise une procédure de recherche locale à chaque individu, il est appelé « algorithme mémétique ».

Dans la terminologie historique, on cherche à maximiser la valeur de la fonction objective, à l'aide d'opérateurs montrant des comportements d’exploitations ou d’exploration. Ces termes correspondent aux notions d'intensification et à la diversification, plutôt utilisés dans le domaine des métaheuristiques, où l'on cherche en général à minimiser la valeur de la fonction objectif. Néanmoins, ces deux domaines sont tout à fait similaires, les algorithmes évolutionnaires ayant tendance à être classés parmi les métaheuristiques.

Dans sa version de base, l'algorithme manipule itérativement un ensemble de vecteurs de variables réelles, à l'aide d'opérateurs de mutation et de sélection. La sélection s'effectue par un choix déterministe des meilleurs individus, selon l'échelle de valeur de la fonction objectif. L'étape de mutation est classiquement effectuée par l'ajout d'une valeur aléatoire, tirée au sein d'une distribution normale. Une particularité caractéristique de ces algorithmes est l'auto-adaptation de la matrice de variance-covariance de la distribution normale.

Un algorithme représentatif des stratégies d'évolution est l'évolution différentielle. Dans cette classe de méthode, on utilise la différence pondérée entre sous-populations pour biaiser un opérateur de mutation différentiel.

Historiquement, ces algorithmes étaient conçus pour des problèmes d'apprentissage à partir d'automates à états finis et n'utilisaient que des opérateurs de mutation et de remplacement. Cependant, aujourd'hui ils ne se limitent plus à une représentation, mais n'utilisent toujours pas d'opérateur de croisement. Ils diffèrent des stratégies d'évolution en ce qu'ils privilégient des opérateurs de remplacement stochastiques.

Les algorithmes génétiques sont les plus populaires des algorithmes évolutionnaires. Ils différencient explicitement le génotype du phénotype, le génotype étant généralement codé de façon binaire. Le choix du codage du génotype (la façon dont il est relié au phénotype) est crucial pour un algorithme génétique. Classiquement, ils utilisent un opérateur de sélection proportionnel, un remplacement générationnel et l'opérateur de croisement est l'opérateur principal.

Des algorithmes évolutionnaires utilisant d'autres représentations et opérateurs sont souvent appelés algorithmes génétiques, bien que les spécialistes évitent cet abus de langage.

Ces algorithmes utilisent une représentation en arbres d'expressions logiques, du fait qu'ils sont historiquement appliqués à l'apprentissage statistique et la modélisation. Ils utilisent pour ce faire le même algorithme de base que les algorithmes génétiques. Cependant, la programmation génétique s'intéresse spécifiquement à la construction automatique de programmes.

Contrairement aux algorithmes évolutionnaires « classiques », le cœur de ces méthodes consiste à estimer les relations entre les différentes variables d'un problème d'optimisation, grâce à l'estimation d'une distribution de probabilité, associée à chaque point de l'échantillon. Ils n'emploient donc pas d'opérateurs de croisement ou de mutation, l'échantillon étant directement construit à partir des paramètres de distribution, estimés à l'itération précédente.

• (fr) Johann Dréo, Alain Petrowski, Éric Taillard, Patrick Siarry, Métaheuristiques pour l’optimisation difficile, Français, Éd. Eyrolles, Paris, septembre 2003, Broché, 356 pages, (ISBN 2-212-11368-4).
• (en) A. E. Eiben, M. Schoenauer, Evolutionary computing, Information Processing Letters, n^o 82, pages 1 à 6, 2002.

• Certains systèmes immunitaires artificiels peuvent être vus comme des algorithmes évolutionnaires et des métaheuristiques d'optimisation.
• Ils sont parfois également appelés algorithmes mémétiques, car les solutions mathématiques manipulées sont parfois plus proches de la culture que de la biologie.

• Portail de l'informatique théorique