Algorithme de Risch

L'algorithme de Risch a pour but d'intégrer des fonctions élémentaires, c'est-à-dire des fonctions obtenues par composition d'exponentielles, de logarithmes, de radicaux, des fonctions trigonométriques[1], et des quatre opérations arithmétiques (+ − × ÷). Laplace résolut ce problème pour le cas des fonctions rationnelles, en montrant que la primitive d'une telle fonction est somme d'une fraction rationnelle et de multiples de logarithmes de fractions rationnelles. L'algorithme suggéré par Laplace est généralement décrit dans les manuels de calcul intégral[2] ; en tant que programme informatique, il fut finalement implémenté dans les années 1960.

Entre 1833 et 1841, Liouville formula rigoureusement le problème que résout l'algorithme de Risch. Il montra (par des méthodes analytiques) que s'il existe une solution élémentaire g à l'équation g ′ = f, alors il y a des constantes α_i et des fonctions élémentaires[3] u_i et v telles que la solution soit de la forme

${\displaystyle g=v+\sum _{i<n}\alpha _{i}\,\ln(u_{i})}$

(c'est le théorème de Liouville-Rosenlicht). Risch développa une méthode permettant de ne considérer qu'un ensemble fini de fonctions élémentaires ayant la forme donnée par Liouville.

L'intuition amenant à l'algorithme de Risch vient du comportement de la dérivée des exponentielles et des logarithmes. Ainsi, pour f e^g, on a

${\displaystyle (f\cdot e^{g})'=(f^{\prime }+f\cdot g^{\prime })\cdot e^{g},\,}$

donc si e^g apparaît dans une primitive, e^g devrait déjà figurer dans la fonction initiale. De même, comme

${\displaystyle (f\cdot \ln ^{n}g)'=f^{\prime }\ln ^{n}{g}+nf{\frac {g^{\prime }}{g}}\ln ^{n-1}{g}}$,

si lnⁿg apparaît, seules les puissances inférieures du logarithme devraient être dans la fonction initiale.

Axiom calculant la primitive de l'exemple

L'existence (ou non) d'une primitive élémentaire est extrêmement sensible aux détails exacts de la fonction à intégrer. Ainsi, la fonction suivante a une primitive élémentaire :

${\displaystyle f(x)={\frac {x}{\sqrt {x^{4}+10x^{2}-96x-71}}}.}$

Mais ce n'est plus le cas si 71 est remplacé par 72. La raison profonde en est que le groupe de Galois de

${\displaystyle x^{4}+10x^{2}-96x-71\,}$

est D(4), c'est-à-dire qu'il est engendré par les permutations (1 2 3 4) et (1 3), et contient huit éléments (comme celui de x⁴ − 2), alors que le groupe de Galois de

${\displaystyle x^{4}+10x^{2}-96x-72\,}$

est S(4), engendré par les permutations (1 2), (1 3), (1 4), et contient 24 éléments.

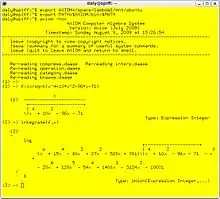
Transformer la procédure de décision de Risch en un algorithme pouvant être exécuté par un ordinateur, et ce de manière efficace, est une tâche complexe demandant l'utilisation d'heuristiques, et de nombreuses améliorations. De fait, en 2008, on ne connaissait aucun logiciel exécutant l'algorithme complet, quoique plusieurs systèmes de calcul formel utilisent une implémentation partielle. Le système Axiom est le seul annonçant avoir complètement implémenté la partie négative de l'algorithme, c'est-à-dire que si Axiom répond « non », la primitive demandée ne peut s'exprimer à l'aide des fonctions élémentaires, mais dans de nombreux cas, Axiom refuse de se prononcer.

Par exemple, Axiom (voir l'illustration ci-dessus) peut trouver une primitive élémentaire pour la fonction de l'exemple précédent :

${\displaystyle f(x)={\frac {x}{\sqrt {x^{4}+10x^{2}-96x-71}}}}$

La solution renvoyée est:

${\displaystyle {\begin{aligned}F(x)=-{\frac {1}{8}}\ln &\,{\Big (}(x^{6}+15x^{4}-80x^{3}+27x^{2}-528x+781){\sqrt {x^{4}+10x^{2}-96x-71}}{\Big .}\\&-{\Big .}(x^{8}+20x^{6}-128x^{5}+54x^{4}-1408x^{3}+3124x^{2}+10001){\Big )}+C.\end{aligned}}}$

Beaucoup d'autres programmes ne peuvent trouver une primitive pour cette fonction qu'à l'aide d'intégrales elliptiques, des fonctions spéciales que l'algorithme de Risch ne sait pas traiter.

La fonction suivante[4] est un exemple plus complexe, que la plupart des logiciels n'arrivent pas à intégrer en se limitant aux fonctions élémentaires :

${\displaystyle f(x)={\frac {x^{2}+2x+1+(3x+1){\sqrt {x+\ln x}}}{x\,{\sqrt {x+\ln x}}(x+{\sqrt {x+\ln x}})}}}$

Pourtant, la primitive de cette fonction a une forme assez simple :

${\displaystyle F(x)=2({\sqrt {x+\ln x}}+\ln(x+{\sqrt {x+\ln x}}))+C.}$

L'algorithme de Risch appliqué à des fonctions élémentaires quelconques n'est en fait qu'un semi-algorithme, parce qu'il doit vérifier à certaines étapes si des coefficients d'expressions partielles obtenues sont nuls ou non. Même pour des expressions assez simples, on sait que cette question est indécidable : c'est le théorème de Richardson.

Il faut remarquer que cette difficulté se présente également pour de nombreux algorithmes apparemment sans problème, tel que l'algorithme de division des polynômes[5]. C'est pourquoi, en pratique, on utilise des heuristiques pour déterminer (avec un risque d'erreur) si ces simplifications ont lieu ou non.

On a pu étendre l'algorithme de Risch (tout comme le théorème de Liouville) à certaines classes de fonctions non élémentaires ; on consultera en particulier à ce sujet Bronstein 2005.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Risch algorithm » (voir la liste des auteurs).
• (en) R. H. Risch, « The solution of the problem of integration in finite terms », Bulletin of the American Mathematical Society, vol. 76, n^o 3,‎ 1970, p. 605–608 (lire en ligne, consulté le 9 mai 2018)
• (en) Maxwell Rosenlicht, « Integration in finite terms », American Mathematical Monthly, Mathematical Association of America, vol. 79, n^o 9,‎ 1972, p. 963–972 (lire en ligne)
• (en) Geddes, Czapor, Labahn, Algorithms for Computer Algebra, Boston, Kluwer Academic Publishers, 1992, 6^e éd., 586 p. (ISBN 978-0-7923-9259-0)
• (en) Manuel Bronstein, Symbolic Integration I : Transcendental Functions, Springer, 2005, 2^e éd., 325 p. (ISBN 978-3-540-21493-9, LCCN 2004110974)
• (en) Manuel Bronstein, Symbolic Integration Tutorial, 1998 (lire en ligne)
• (en) Bhatt, Bhuvanesh, « Risch Algorithm », sur MathWorld

• Table d'intégrales
• Théorème de Liouville (algèbre différentielle)
• Axiom (logiciel)

• Portail de l'analyse
• Portail de l’informatique
• Portail de l'informatique théorique