Algorithme des k-médoïdes
En statistiques, un médoïde[2] est le représentant le plus central d'une classe. L'algorithme des k-médoïdes est un algorithme de partitionnement plus robuste vis-à-vis des données aberrantes (outliers) que celui des k-means (k-moyennes).
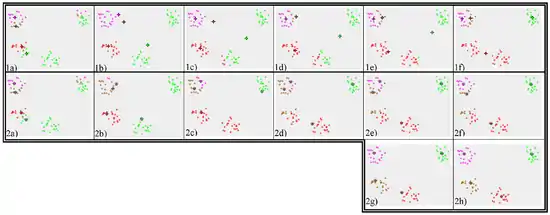
K-medoids versus k-means. Les figures 1a-1f présentent représente un cas typique de la convergence de l'algorithme des k-moyennes vers un minimum local. Le résultat de la classification par les k-moyennes est ici en contradiction avec le partitionnement évident des données. Les figures 2a-2h présente l'algorithme des k-medoids avec la même configuration initiale des medoïdes (Fig. 2a) et converge vers la classification la plus évidente. Les petits cercles représentent les données, les étoiles à 4 branches représentent les moyennes, et les étoiles à neuf branches les médoïds[1]
Algorithme
Comme les k-moyennes, l'algorithme des k-médoïdes minimise l'erreur quadratique moyenne qui est la distance entre les points de la classe et le point central (ou médoïde).
Voir aussi
Références
- The illustration was prepared with the Java applet, E.M. Mirkes, K-means and K-medoids: applet. University of Leicester, 2011.
- Stéphane Tufféry, Data Mining et statistique décisionnelle, Éditions Technip, page 244
Bibliographie
- Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.