Analyseur cubique

L’analyseur cubique est un outil graphique permettant d’estimer la valeur du paramètre de maille d’un cristal ayant un réseau de Bravais cubique et de déterminer les indices de Miller des plans diffractés. La technique de l’analyseur cubique utilise un graphique mettant en relation le paramètre de maille $a$ et la distance interréticulaire d_hkl. Cet outil permet une analyse rapide d’un cliché de diffraction par rayons X.

Relation mathématique

Le principe de l’analyseur cubique repose sur le fait que les trois paramètres de maille du cristal cubique sont égaux : $a$ = $b$ = $c$ . Cette particularité permet de simplifier l’équation de la distance interréticulaire, la distance entre deux plans d’indices de Miller (hkl), sous la forme suivante :

$d_{hkl}={\frac {a}{\sqrt {h^{2}+k^{2}+l^{2}}}}$

En réorganisant cette équation afin d’avoir $a$ en fonction de d_hkl, on obtient :

$a=d_{hkl}\cdot {\sqrt {h^{2}+k^{2}+l^{2}}}$

Puisque les valeurs des indices des plans hkl sont entières par définition, il est possible de tracer une droite pour chaque triplet d’indices hkl possibles. Voici un exemple d’analyseur cubique :

Exemple d’analyseur cubique

Principe d'utilisation

L’utilisation de l’analyseur cubique se fait en trois étapes. La première consiste à déterminer les valeurs de d_hkl pour chaque pic ou chaque anneau de diffraction, selon la méthode de diffraction utilisée. Ces valeurs sont obtenues préalablement par l’application de la loi de Bragg sous la forme :

$d_{hkl}={\frac {\lambda }{2\cdot \sin \theta }}$

La seconde étape consiste à tracer sur le graphique de l’analyseur cubique une droite verticale pour chaque valeur de d_hkl à la position correspondante sur l’axe des abscisses. Finalement, il faut trouver la ligne horizontale pour laquelle chaque ligne verticale de d_hkl intercepte une ligne oblique représentant une famille de plan hkl. La lecture sur l’axe des ordonnées de la meilleure ligne horizontale possible, c’est-à-dire qui minimise l’écart entre les interceptions et la droite horizontale, définit la valeur du paramètre de maille estimé.

Exemple d’utilisation d’un analyseur cubique

Considérons, à fin d’exemple, les données suivantes, préalablement obtenues à partir d’un cliché de diffraction d’un matériau cubique et par l’utilisation de la loi de Bragg :

Numéro de la raie	d_hkl [Å]
1	1.39
2	1.46
3	1.72
4	2.4
5	2.76

On trace une droite verticale pour chacune des valeurs de d_hkl sur l’analyseur cubique :

On trace les verticales sur l'analyseur cubique

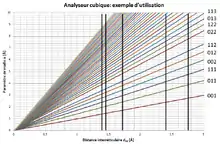
On cherche ensuite la droite horizontale pour laquelle chaque verticale tracée précédemment intercepte une ligne d’indice. Dans notre cas, on remarque que la meilleure droite d’approximation est pour $a$ = 4.8 Å :

Recherche du meilleur estimateur

On peut donc estimer la valeur du paramètre de maille $a$ de notre échantillon à 4.8 Å. On peut aussi indexer les indices, les valeurs des indices de Miller pour chacune des raies observées :

Numéro de la raie	Indices de Miller (hkl)
1	222
2	133
3	022
4	002
5	111

Puisque tous les indices de tous les plans observés ont des indices hkl de même parité, les conditions d’extinctions indique que le matériau à une structure cubique à faces centrées.

Référence

(en) Laboratory Experiments in X-Ray Crystallography ; L.V. Azaroff, R.J. Donahue ; McGraw-Hill (1969), p. 67-71

Portail de la physique
Portail de la chimie
Portail des sciences des matériaux
Portail des minéraux et roches

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.