Antiferromagnétisme

Dans un matériau antiferromagnétique, on peut diviser la structure cristalline en plusieurs sous-réseaux de moments magnétiques différents, mais dont la somme vectorielle de ces moments est nulle.

Exemple de l'oxyde de Manganèse

${\displaystyle \Sigma {\vec {M_{i}}}={\vec {0}}}$

Dans le cas simple d'un antiferromagnétique divisible en deux sous-réseaux A et B, les moments de ceux-ci sont exactement égaux et opposés en direction, soit

${\displaystyle {\vec {M}}={\vec {M_{A}}}+{\vec {M_{B}}}={\vec {0}}}$

Variation de la susceptibilité en fonction de la température.

Dans ces matériaux, la variation de la susceptibilité va être la conséquence d'une lutte entre l'énergie d'interaction d'échange et l'énergie provenant de l'agitation thermique. Les moments magnétiques qui se compensent parfaitement sans agitation thermique, vont se désordonner légèrement avec la température de façon à créer un moment magnétique qui va croître jusqu'à une température ${\displaystyle T_{N}}$ dite température de Néel. Au-dessus de la température de Néel (${\displaystyle T_{N}}$), l'agitation thermique est trop importante et les moments magnétiques si désordonnés que la susceptibilité diminue. On comprend donc la variation de la susceptibilité en fonction de la température, qui augmente jusqu'à ${\displaystyle T_{N}}$ puis diminue.

On rappelle que la température de Néel représente la température de passage du comportement antiferromagnétique au comportement paramagnétique d'un matériau antiferromagnétique. En supposant qu’un antiferromagnétique peut se décomposer en deux sous-réseaux A et B, le coefficient d’échange (lié à l'interaction d'échange) entre deux réseaux antiparallèles est donné par ${\displaystyle w_{a,b}=w_{b,a}=w}$ et par ${\displaystyle w_{a,a}=w_{b,b}=w'}$ pour un échange dans un même réseau.

On peut montrer que la température de Néel vaut ${\displaystyle T_{N}=C(w+w')}$.

Démonstration:

On a donc le champ magnétique total agissant respectivement sur A et B :

${\displaystyle H_{A}=H-wM_{B}+w'M_{A}}$

${\displaystyle H_{B}=H-wM_{A}+w'M_{B}}$

Avec H le champ imposé au matériau, M_A et M_B respectivement le moment magnétique des sous-réseaux A et B.

Comme à la température de Néel, les propriétés paramagnétiques commencent à apparaître, on peut écrire :

${\displaystyle M_{A}={\frac {C}{T_{n}}}H_{A}}$

${\displaystyle M_{B}={\frac {C}{T_{n}}}H_{B}}$

avec la constante Curie telle que

${\displaystyle C={\frac {\mu Nm_{0}^{2}}{3k_{b}}}}$

Donc à champ nul (H=0), si on injecte les formules du moment magnétique, on retrouve le système suivant :

${\displaystyle (1-{\frac {w'C}{T_{N}}})H_{B}+{\frac {wC}{T_{N}}}H_{A}=0}$

${\displaystyle (1-{\frac {w'C}{T_{N}}})H_{A}+{\frac {wC}{T_{N}}}H_{B}=0}$

Ainsi à champ nul (H=0), le système des deux équations linéaires précédentes a une solution telle que le déterminant des coefficients de celles-ci soit nul. Ainsi, la température maximale que l’on peut trouver est donnée par l’expression :

${\displaystyle (1-{\frac {Cw'}{T_{N}}})^{2}-({\frac {Cw}{T_{N}}})^{2}=0}$

Ainsi en découle la température de Néel

${\displaystyle T_{N}=C(w+w')}$

Si au-dessus de la température de Néel T_N, on considère qu’un antiferromagnétique est constitué de deux sous-réseaux ferromagnétiques, on montre d’après la loi de Curie-Weiss,

que ${\displaystyle M=M_{A}+M_{B}={\frac {2C}{(T-\theta _{p})}}}$

avec C la constante de Curie, et ${\displaystyle \theta _{p}}$ une constante de température inférieure à T_N

Diffraction d'un faisceau incident sur un plan atomique

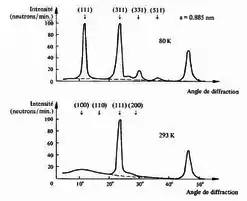
Expérimentalement, on peut mettre en évidence l'apparition de ce désordre magnétique (tendance des moments magnétiques à s'orienter aléatoirement) grâce à la diffraction de neutrons. En effet, si les électrons peuvent diffracter selon la loi de Bragg grâce aux interactions électrostatiques des atomes dans les structures cristallines, on peut avoir une diffraction des neutrons par interaction des moments magnétiques, lorsqu'ils possèdent aussi un certain ordre. Ainsi, plus le matériau est ordonné, plus il comporte de plans de diffraction et donc un nombre de pics élevé en intensité en fonction de l'angle de diffraction. On rappelle qu'il y a diffraction lorsqu'on respecte les conditions de Bragg: ${\displaystyle 2d_{hkl}sin(\theta )=n\lambda }$,

Expérience de diffraction neutronique

avec d_hkl: la distance entre les plans de la famille hkl,

θ: l'angle incident du faisceau,

λ: la longueur d'onde du faisceau

n: l'ordre du plan diffracté

Ci-contre, on peut voir le résultat obtenu à partir d'un échantillon d'oxyde de manganèse et des neutrons monocinétiques de 0,074 eV, en fonction de la température. On voit bien qu'avec l'agitation thermique, les plans de diffraction changent et que moins de pics apparaissent, témoignant de la disparition de plans de diffraction et donc la disparition de l'ordre antiferromagnétique.

La susceptibilité d'un antiferromagnétisme est faible. À titre d'exemple, elle est de 3,6 × 10⁻⁶ pour le chrome. La courbe de la valeur de l'aimantation M en fonction du champ magnétique H est différente selon l'angle entre les spins et H au début de l'application. Lorsqu'on augmente le champ magnétique, l'aimantation a tendance à s'aligner dans la direction du champ magnétique tandis que l'interaction d'échange s'y oppose. L'énergie d'échange est tellement grande qu'il faut appliquer un champ de plusieurs centaines de teslas pour saturer un matériau antiferromagnétique. Nous allons illustrer ce propos avec deux cas extrêmes : quand H est parallèle aux spins et lorsque H est perpendiculaire aux spins à une température donnée.

Aimantation en fonction du champ initialement perpendiculaire

Orientation des spins en fonction de la direction du champ

• Ferromagnétisme

• Portail de la physique