Antiparallèle (mathématiques)

Étant donné deux droites ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$, les droites ${\displaystyle l_{1}}$ et ${\displaystyle l_{2}}$ sont dites anti-parallèles par rapport à ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$ si ${\displaystyle \angle 1=\angle 2}$ sur dans la figure 1. De plus, si ${\displaystyle l_{1}}$ et ${\displaystyle l_{2}}$ sont anti-parallèles par rapport à ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$, alors ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$ sont également anti-parallèles par rapport à ${\displaystyle l_{1}}$et ${\displaystyle l_{2}}$.

Dans tout quadrilatère inscriptible, deux côtés opposés sont anti-parallèles par rapport aux deux autres côtés (figure 2).

Deux droites ${\displaystyle l_{1}}$ et ${\displaystyle l_{2}}$ sont antiparallèles à un angle si et seulement s'ils font le même angle en sens opposés avec la bissectrice de cet angle (figure 3).

Fig.1: ${\displaystyle l_{1}}$et ${\displaystyle l_{2}}$ sont anti-parallèles par rapport à ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$ si ${\displaystyle \angle 1=\angle 2}$.

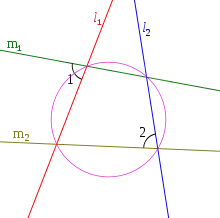Fig.2: Dans tout quadrilatère cyclique, deux côtés opposés sont anti-parallèles par rapport aux deux autres côtés.

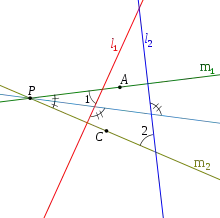Fig.3: Notez que les angles précédents 1 et 2 sont toujours égaux.

Dans un espace euclidien, deux vecteurs, sont antiparallèles s'ils sont supportés par des droites parallèles et sont des directions opposées.[1] Dans ce cas, l'un des vecteurs est le produit de l'autre par un scalaire négatif.

1. La droite joignant les pieds de deux hauteurs d’un triangle est antiparallèle au côté opposé.
2. La tangente à un cercle circonscrit à un sommet est antiparallèle avec le côté opposé.
3. Le rayon du cercle circonscrit à un sommet d'un triangle est perpendiculaire à toutes les droites étant antiparallèle avec le côté opposé.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Antiparallel (mathematics) » (voir la liste des auteurs).

• AB Ivanov, Encyclopédie de Mathématiques - (ISBN 1-4020-0609-8)
• Weisstein, Eric W. "Antiparallel." From MathWorld - Une ressource Web Wolfram.

• Portail de la géométrie