Appariement à 3 dimensions

En mathématiques, et notamment en théorie des graphes, un appariement à 3 dimensions (en anglais : 3-dimensional matching) est une généralisation du couplage (aussi appelé appariement en dimension 2 ) à une situation ternaire qui, techniquement, est celle des hypergraphes dits 3-uniformes. Trouver un appariement à 3 dimensions de taille maximum est un problème NP-difficile bien connu en théorie de la complexité informatique.

Appariement à 3 dimensions. (a) Donnée T. (b)–(c) Deux solutions. (c) est de taille maximum.

Définition

Soient $X,Y$ et $Z$ trois ensembles finis disjoints, et soit $T$ un sous-ensemble de $X\times Y\times Z$ . Ainsi, $T$ est composé de triplets $(x,y,z)$ , avec $x\in X,y\in Y$ et $z\in Z$ . Une partie $M\subseteq T$ est un appariement à 3 dimensions si la propriété suivante est vérifiée : pour toute paire de triplets $(x_{1},y_{1},z_{1})$ et $(x_{2},y_{2},z_{2})$ distincts de $M$ , on a $x_{1}\neq x_{2}$ , $y_{1}\neq y_{2}$ et $z_{1}\neq z_{2}$ . En d'autres termes, si deux triplets diffèrent sur une composante, ils doivent différer sur toutes leurs composantes.

Exemple

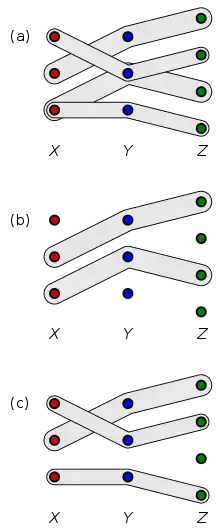
La figure à droite illustre un appariement à 3 dimensions. L'ensemble $X$ est représenté par des points rouges, $Y$ par des points bleus et $Z$ par des points verts. La figure (a) montre l'ensemble $T$ donné ; chaque triplet est dessiné dans une zone grisée. La figure (b) montre un appariement à 3 dimensions composé de deux éléments, et la figure (c) montre un appariement composé de trois éléments.

L'appariement de la figure (c) est de taille maximum : il n'en existe pas de taille plus grande, alors que l'appariement de la figure (b), tout en n'étant pas de taille maximum, est maximal : il ne peut pas être agrandi en un appariement plus grand.

Comparaison avec le couplage

Un couplage, ou appariement à 2 dimensions, peut être défini de manière tout à fait analogue : soient $X$ et $Y$ deux ensemble finis disjoints, et soit $T$ une partie de $X\times Y$ . Une partie $M\subseteq T$ est un couplage si, pour toute paire de couples distincts $(x_{1},y_{1})$ et $(x_{2},y_{2})$ de $M$ , on a $x_{1}\neq x_{2}$ et $y_{1}\neq y_{2}$ .

Dans le cas de l’appariement en dimension 2, l'ensemble $T$ peut être interprété comme l'ensemble des arêtes d'un graphe biparti $G=(X\cup Y,T)$ , chaque arête de $T$ reliant un sommet de $X$ à un sommet de $Y$ . Un appariement à 2 dimensions est alors couplage dans le graphe $G$ , c'est-à-dire un ensemble d'arêtes deux-à-deux non adjacentes.

De même, un appariement à 3 dimensions peut être interprété comme une généralisation des couplages aux hypergraphes : les ensembles $X,Y$ et $Z$ contiennent les sommets, chaque triple de $T$ est une hyper-arête, et l'ensemble $M$ est formé d'hyper-arêtes deux-à-deux disjointes, c'est-à-dire sans sommet commun.

Comparaison avec le set packing

Un appariement à 3 dimensions est un cas particulier du set packing: on peut interpréter chaque triplet $(x,y,z)$ de $T$ comme un sous-ensemble $\{x,y,z\}$ de $X\cup Y\cup Z$ ; un appariement à 3 dimensions $M$ consiste alors en des sous-ensembles deux-à-deux disjoints.

Problème de décision

En théorie de la complexité informatique, le problème de l'appariement à 3 dimensions est le nom du problème de décision suivant : étant donné un ensemble $T$ et un entier k; décider s'il existe un appariement à 3 dimensions $M\subseteq T$ avec au moins k éléments.

Ce problème de décision est connu pour être NP-complet : c'est l'un des fameux 21 problèmes NP-complets de Karp[1]. Il existe toutefois des algorithmes polynomiaux pour ce problème dans des cas particuliers, comme celui des hypergraphes « denses »[2]^,[3].

Le problème est NP-complet même dans le cas particulier où $k=|X|=|Y|=|Z|$ [1]^,[4]^,[5]. Dans ce cas, un appariement à 3 dimensions n'est pas seulement un set packing mais aussi un problème de la couverture exacte : l'ensemble $M$ couvre chaque élément de $X,Y$ et $Z$ une fois exactement[6].

Problème d'optimisation

Un appariement à 3 dimensions maximum est un appariement à 3 dimensions de taille maximum. En théorie de la complexité, c'est aussi le nom du problème d'optimisation combinatoire suivant : étant donné $T$ , trouver un appariement à 3 dimensions $M$ de taille maximum.

Comme le problème de décision est NP-complet, le problème d'optimisation est NP-difficile, et il n'existe donc vraisemblablement pas d'algorithme polynomial pour trouver un appariement à 3 dimensions maximum, alors qu'il existe des algorithmes efficaces en temps polynomial pour la dimension 2, comme l'algorithme de Hopcroft et Karp.

Algorithmes d'approximation

Le problème est APX-complet ; en d'autres termes, il est difficile de l'approximer avec un facteur constant[7]^,[8]^,[9]. En revanche, pour toute constante $\varepsilon >0$ , il existe un algorithme d'approximation en temps polynomial de facteur $3/2+\varepsilon$ [7]^,[8].

Il existe un algorithme polynomial très simple pour calculer une appariement à 3 dimensions avec un facteur d'approximation 3 : il suffit de trouver un appariement à 3 dimensions quelconque qui ne peut être augmenté (un appariement maximal)[9]. Il n'est pas forcément maximum, mais tout comme une couplage maximal est un couplage maximum à un facteur 1/2 près, un appariement à 3 dimensions maximal est maximum à un facteur 1/3 près.

Notes et références

Karp 1972.
Karpinski, Rucinski et Szymanska 2009
Keevash, Knox et Mycroft 2013
Garey et Johnson 1979, Section 3.1 et Problème SP1 dans Appendix A.3.1.
Korte et Vygen 2006, Section 15.5.
Papadimitriou et Steiglitz 1998, Section 15.7.
Crescenzi et al. 2000.
Ausiello et al. 2003, Problème SP1 de l'Appendice B.
Kann 1991.

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « 3-dimensional matching » (voir la liste des auteurs).

Voir aussi

Articles connexes

Bibliographie

Giorgio Ausiello, Pierluigi Crescenzi, Giorgio Gambosi, Viggo Kann, Alberto Marchetti-Spaccamela et Marco Protasi, Complexity and Approximation : Combinatorial Optimization Problems and Their Approximability Properties, Springer, 2003.
Pierluigi Crescenzi, Viggo Kann, Magnús Halldórsson, Marek Karpinski et Gerhard Woeginger, « Maximum 3-dimensional matching », dans A Compendium of NP Optimization Problems, 2000 (lire en ligne).
(en) Michael Garey et David S. Johnson, Computers and Intractability : A Guide to the Theory of NP-Completeness, W.H. Freeman, 1979 (ISBN 0-7167-1045-5).
Viggo Kann, « Maximum bounded 3-dimensional matching is MAX SNP-complete », Information Processing Letters, vol. 37, n^o 1,‎ 1991, p. 27–35 (DOI 10.1016/0020-0190(91)90246-E).
(en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103
Marek Karpinski, Andrzej Rucinski et Edyta Szymanska, « The Complexity of Perfect Matching Problems on Dense Hypergraphs », ISAAC '09 Proceedings of the 20th International Symposium on Algorithms,‎ 2009, p. 626-636 (DOI 10.1007/978-3-642-10631-6_64).
Peter Keevash, Fiachra Knox et Richard Mycroft, « Polynomial-Time perfect matchings in dense hypergraphs », STOC '13 Proceedings of the forty-fifth annual ACM symposium,‎ 2013, p. 311-320 (DOI 10.1145/2488608.2488647).
Bernhard Korte et Jens Vygen, Combinatorial Optimization : Theory and Algorithms, Springer, 2006, 3^e éd..
Christos H. Papadimitriou et Kenneth Steiglitz, Combinatorial Optimization : Algorithms and Complexity, Dover Publications, 1998.

Portail de l'informatique théorique
Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[karp72-1] Karp 1972.

[Karpinski2009-2] Karpinski, Rucinski et Szymanska 2009

[3] Keevash, Knox et Mycroft 2013

[garey79-4] Garey et Johnson 1979, Section 3.1 et Problème SP1 dans Appendix A.3.1.

[korte06-5] Korte et Vygen 2006, Section 15.5.

[papadimitriou98-6] Papadimitriou et Steiglitz 1998, Section 15.7.

[compendium-7] Crescenzi et al. 2000.

[ausiello03-8] Ausiello et al. 2003, Problème SP1 de l'Appendice B.

[kann91-9] Kann 1991.