Arbre de Van Emde Boas

Les clés utilisées dans un arbre vEB sont des entiers de ${\displaystyle m}$ bits, donc des entiers compris entre 0 et ${\displaystyle M-1}$, où ${\displaystyle M=2^{m}}$. Ce nombre est aussi le nombre maximal de données contenues dans un tel arbre. On suppose, pour simplifier, que ${\displaystyle m}$ lui-même est un puissance de 2.

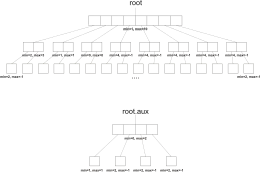
Un arbre vEB T de taille ${\displaystyle M}$, à clés dans ${\displaystyle \{0,\ldots ,M-1\}}$, est composé

• d'un arbre vEB de taille ${\displaystyle {\sqrt {M}}}$ appelé le « sommaire », ou « top » et noté T.top
• d'un tableau, noté aussi « bottom », de ${\displaystyle {\sqrt {M}}}$ arbres « feuilles » vEB de taille ${\displaystyle {\sqrt {M}}}$, indicé par les entiers de ${\displaystyle \{0,\ldots ,{\sqrt {M}}-1\}}$, notés T.bottom[0], etc., T.bottom[${\displaystyle {\sqrt {M}}-1}$].

L'arbre sommaire et les arbres feuilles sont de taille ${\displaystyle {\sqrt {M}}}$ et ont pour clés des entiers de ${\displaystyle m/2}$ bits, composés à partir des clés pour l'arbre T : Si ${\displaystyle x}$ est un entier sur ${\displaystyle m}$ bits, alors ${\displaystyle x=a2^{m/2}+b}$, où ${\displaystyle a}$ est l'entier écrits sur les ${\displaystyle m/2}$ bits de poids fort de ${\displaystyle x}$, et ${\displaystyle b}$ l'entier représenté par les ${\displaystyle m/2}$ bits de poids faible. Les entiers ${\displaystyle a}$ et ${\displaystyle b}$ sont aussi notés de manière plus fonctionnelle hi(x) et lo(x). L'arbre sommaire contient, pour ${\displaystyle a}$, un pointeur vers l'arbre feuille d'indice ${\displaystyle a}$, si cet arbre n'est pas vide, et la valeur associée à la clé ${\displaystyle b}$ dans l'arbre feuille est la valeur cherchée. Ainsi, la valeur associée à x dans T est la valeur associée à ${\displaystyle b}$ dans l'arbre T.bottom[a], ou encore T.bottom[hi(x)].lo(x).

De plus, un arbre vEB T maintient deux valeurs ${\displaystyle T.\min }$ et ${\displaystyle T.\max }$ qui contiennent la plus petite et la plus grande valeur présente dans l'arbre. Ces valeurs ne figurent pas ailleurs dans l'arbre. Si l'arbre est vide, on pose ${\displaystyle T.\min =M}$ et ${\displaystyle T.\max =-1}$. Une variante consiste à maintenir un champ additionnel T.taille qui simplifie ce test.

Un arbre vEB réalise les opérations d'un tableau associatif ordonné, ce qui comprend les opérations usuelles d'un tel tableau, et deux autres opérations, relatives à l'ordre, qui sont suivant et précédent[4] qui donnent l'élément immédiatement supérieur respectivement inférieur présent dans l'arbre ; en plus les opérations minimum et maximum retournent respectivement le plus petit et le plus grand élément contenu dans l'arbre. Ces deux éléments sont trouvés en temps constant O(1), parce qu'ils figurent à des emplacements séparés dans l'arbre[5].

• insérer : insère la paire (clé,valeur) ;
• supprimer : supprime la paire (clé,valeur) donnée par la clé ;
• chercher : retourne la valeur associée à une clé donnée ;
• suivant : retourne la paire (clé, valeur) avec la plus petite clé strictement supérieure à la clé donnée ;
• précédent : retourne la paire (clé, valeur) avec la plus petite clé strictement inférieur à la clé donnée ;
• minimum : retourne la plus petite valeur contenue dans l'arbre ;
• maximum : retourne la plus grande valeur contenue dans l'arbre .

L'hypothèse que m est une puissance de 2 n'est pas indispensable : le fonctions hi(x) et lo(x) peuvent aussi bien retourner l'entier formé des ${\displaystyle \lceil m/2\rceil }$ plus forts bits et des ${\displaystyle \lfloor m/2\rfloor }$ plus faibles bits de x,sans changer l'algorithme et son évaluation en temps.

L'implémentation décrite ci-dessus occupe une place en O(M) = O(2^m). La formule de récurrence pour la place prise par un arbre vEB est

${\displaystyle S(M)=O({\sqrt {M}})+({\sqrt {M}}+1)\cdot S({\sqrt {M}})}$,

ou, en posant ${\displaystyle u={\sqrt {M}}}$,

${\displaystyle S(u^{2})=cu+(1+u)S(u)}$

pour une constante ${\displaystyle c}$. Une résolution directe de ${\displaystyle S(u^{2})=u+(1+u)S(u)}$, avec ${\displaystyle S(4)=1}$, donne

${\displaystyle S(u^{2})=u^{2}-2}$

ce qui prouve, après quelques ajustements, que ${\displaystyle S(M)=O(M)}$[6].

Pour des petits arbres, la place additionnelle requise est importante puisqu'elle les linéaire en fonction de la taille maximale, et non de la taille effective. D'autres variantes ont été proposées pour ces cas, comme les tries. On peut aussi remplaces les tables par une table de hachage, ce qui réduit la place à O(n log M), pour n éléments contenus dans la structure aux dépens d'un coût aléatoire. Les arbres de van Emde Boas peuvent être randomisés pour obtenir une majoration en espace en ${\displaystyle O(n)}$ au lieu de ${\displaystyle S(M)=O(M)}$[6], en remplaçant les tables bottom par des tables de hachage. Une telle modification occupe une place en ${\displaystyle O(n\log \log M)}$. Mais si on utilise ${\displaystyle m/2^{i}}$ bits par entrée dans la table de hachage au i-ème niveau de récursion, la structure ne prend qu'un place en ${\displaystyle O(n)}$. Si un hachage dynamique parfait est employé, les recherches se font toujours en ${\displaystyle O(\log \log M)}$ dans le pire des cas, mais les insertions et suppressions prennent un temps amorti moyen en${\displaystyle O(\log \log M)}$.

D'autres structures, y compris les Y-fast trie (en) et les X-fast trie (en) ont été proposées ; elles ont des complexités en temps comparable pour les requêtes et les modifications, et utilisent aussi des tables de hachage pour réduire la complexité en place.