Arc sinus
En mathématiques, l’arc sinus d'un nombre réel compris (au sens large) entre –1 et 1 est l'unique mesure d'angle en radians dont le sinus vaut ce nombre, et comprise entre –π/2 et π/2.
« Arcsin » redirige ici. Ne pas confondre avec Arsin.

| Notation | |
|---|---|
| Réciproque |
sur |
| Dérivée | |
| Primitives |
| Ensemble de définition |
[−1, 1] |
|---|---|
| Ensemble image | |
| Parité |
impaire |
La fonction qui associe à tout nombre réel compris au sens large entre –1 et 1 la valeur de son arc sinus est notée arcsin (Arcsin[1] ou Asin en notation française, sin−1, asin ou asn en notation anglo-saxonne). Il s'agit alors de la bijection réciproque de la restriction de la fonction trigonométrique sinus à l'intervalle [–π/2, π/2]. Elle fait partie des fonctions circulaires réciproques.
On a donc par définition :
Courbe représentative
Dans un repère cartésien orthonormé du plan, la courbe représentative de la fonction arc sinus est obtenue à partir de la courbe représentative de la restriction de la fonction sinus à l'intervalle [–π/2, π/2] par la réflexion d'axe la droite d'équation y = x.
Relations avec les fonctions circulaires directes
- pour
- pour
- pour
Par contre, seulement pour
La formule générale est où est la partie entière de .
Dérivée
Comme dérivée d'une bijection réciproque, arcsin est dérivable sur ]–1, 1[ et vérifie .Cette formule s'obtient grâce au théorème sur la dérivée d'une bijection réciproque et à la relation .
Relation entre arc sinus et arc cosinus
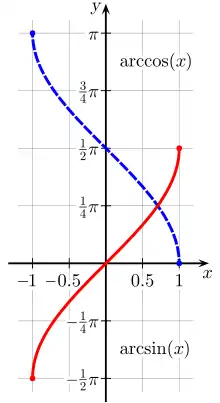
Pour tout réel x entre –1 et 1 : .
Extension aux complexes
De la relation valable pour tout complexe : , on déduit .
D'où l'expression de la fonction arc sinus avec un logarithme complexe : , valable pour .
Le développement en série est alors valable pour tout dans le disque fermé de centre 0 et de rayon 1.
Référence
Voir aussi
- Intégrale de Wallis (pour le développement de )
- (en) Eric W. Weisstein, « Inverse Sine », sur MathWorld
- (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), § 4.4, p. 79-83
- Portail de la géométrie
- Portail de l'analyse