Argument d'un nombre complexe
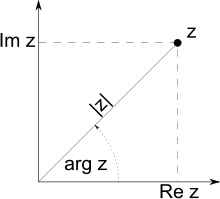
Un argument d’un nombre complexe z non nul est une mesure (en radians, donc modulo 2π) de l'angle entre la demi-droite des nombres réels positifs (l'axe des abscisses) et celle issue de l'origine et passant par le point représenté par z (voir la figure ci-contre).
Définition
Étant donné un nombre complexe z non nul, un argument de z est une mesure (en radians, donc modulo 2π) de l’angle :
où M est l'image de z dans le plan complexe, c'est-à-dire le point d'affixe z.
De manière équivalente, un argument de z est un nombre réel tel que :
- ,
où , et sont respectivement les parties réelle et imaginaire et le module de z.
Souvent, on note un argument du nombre complexe z de façon simplifiée par :
ou plus précisément :
- .
Remarque : en anglais, on parle parfois de la phase[1] ou de l'amplitude[2] d'un nombre complexe : .
Formules de calcul
- Si z n'est pas un imaginaire pur, , où est le conjugué de z et donc :
- si , .
- De manière plus générale, l'argument d'un nombre complexe z non nul peut être entièrement déterminé de la façon suivante :
Propriétés
Soient z, z1 et z2 des complexes non nuls. On a, :
- .
En particulier :
- pour tout réel a non nul :
- pour tout entier relatif n : .
Applications à la géométrie
Si A, B, C et D sont quatre points deux à deux distincts du plan complexe d'affixes respectives a, b, c et d, alors :
Notes et références
- (en) Dictionary of Mathematics, 2002, « phase ».
- (en) Konrad Knopp et Frederick Bagemihl, Theory of Functions Parts I and II, Dover Publications, , 150 p. (ISBN 978-0-486-69219-7), p. 3.
Articles connexes
- Portail des mathématiques