Arithmétique floue
L'arithmétique floue étudie la propagation de l'incertitude dans les expressions arithmétiques. Elle repose sur les principes de la logique floue et plus particulièrement sur les nombres flous, un cas particulier des ensembles flous. L'arithmétique floue est une généralisation de l'arithmétique des intervalles qui utilise les nombres flous pour capturer l'incertitude, là où l'arithmétique des intervalles utilise de simples intervalles de valeurs. L'arithmétique floue s'applique à de nombreux domaines de l'ingénierie, particulièrement lorsque les paramètres des modèles mathématiques sous-jacents sont difficiles à quantifier précisément.
Introduction
La notion d'« incertitude » reflète, au moins en ingénierie, une connaissance relative ou partielle d'un système. La plupart des disciplines scientifiques essaient de construire des modèles mathématiques décrivant une certaine réalité physique. De manière générale, l'incertitude caractérise alors le degré de correspondance entre un modèle et la réalité qu'il décrit, et peut être interprétée comme une erreur potentielle, ou comme un risque, que l'on va chercher à minimiser.
L'incertitude peut concerner le modèle lui-même (par exemple, les équations qui le composent), mais concerne plus généralement les grandeurs manipulées dans le modèle (les paramètres du modèle). Dans ce dernier cas, deux interrogations apparaissent légitimes : d'un côté, on veut évaluer l'incertitude du résultat étant donnée l'incertitude des paramètres ; de l'autre, on veut connaître l'incertitude maximale acceptable pour les paramètres, qui va garantir une incertitude donnée sur le résultat.
Différentes méthodes permettent de modéliser et d'évaluer l'incertitude telles que les intervalles, les probabilités, ou les ensembles aléatoires, ou les ensembles flous utilisés par l'arithmétique dont il est question ici.
Cet article présente les techniques standards utilisées pour mettre en œuvre l'arithmétique floue ainsi que leurs limites, et illustre son utilisation sur quelques expressions arithmétiques simples.
Ensembles flous et nombres flous
La théorie des ensembles flous considère des ensembles dont l'appartenance est graduelle et non pas booléenne comme c'est le cas avec la théorie des ensembles dite « classique ». En effet, la théorie classique implique qu'un élément appartienne ou qu'il n'appartienne pas à un ensemble donné, sans autre possibilité. Par opposition, la théorie des ensembles flous permet d'exprimer le degré d'appartenance par une valeur réelle comprise entre 0 et 1 (1 indiquant que l'élément appartient définitivement à l'ensemble).
Ces ensembles flous sont particulièrement appropriés pour capturer le sens de constructions linguistiques telles que « la vitesse est élevée ». Là où un ensemble classique implique de définir un seuil strict en deçà duquel la vitesse ne sera plus considérée comme « élevée » (par exemple 50 km/h), un ensemble flou définit une fonction qui associe un degré d'appartenance à la vitesse. Sachant que la vitesse est 75 km/h, il devient possible d'établir que la vitesse est approximativement 10 km/h à 50 %.
Ensembles flous
Cette section rappelle brièvement la notion de sous-ensemble flou (fuzzy set en anglais) et leurs propriétés pertinentes dans le cadre de l'arithmétique floue.
Considérons tout d'abord un ensemble infini indénombrable , représentant l'ensemble dans lequel nous allons définir des sous-ensembles flous. Dans le cas de la vitesse évoquée ci-dessus, l'ensemble représentant le domaine des vitesses en km/h, se réduit à l'ensemble des valeurs réelles.
Un sous-ensemble flou [1] sur (représentant par exemple les vitesses dites « élevées ») est défini par sa fonction d'appartenance (ou fonction caractéristique) . Pour une vitesse donnée, v, représente alors le degré d'appartenance de v à .
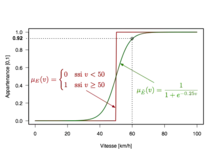
La figure 1 ci-contre illustre la notion de fonction d'appartenance. La courbe verte montre l'évolution du degré d'appartenance : plus la vitesse augmente, plus elle est considérée comme élevée. Cette fonction d'appartenance caractérise donc le sous-ensemble flou des vitesses dite « élevées ». Par opposition, la courbe rouge illustre une fonction d'appartenance qui caractérise un ensemble « classique » équivalent, impliquant un seuil strict (ici, 50 km/h).
Il est important de noter que la fonction d'appartenance , associée à un ensemble flou, n'est pas une densité de probabilité. En dehors d'aspects purement mathématiques[2], une valeur floue reflète le degré avec lequel un évènement se produit (degré de vérité), alors qu'une probabilité reflète le pourcentage de chances que l’évènement se produise (éventualité).
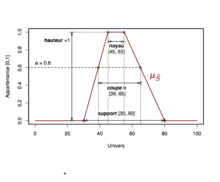
Un ensemble flou considéré sur l'univers se caractérise par les éléments suivants illustrés sur la figure 2 :
- son noyau (core en anglais), qui représente l'ensemble des éléments de pour lesquels le degré d'appartenance est égal à 1. Plus formellement, on définit le noyau par : .
- son support (support en anglais), qui représente le sous-ensemble des éléments de pour lesquels le degré d'appartenance à est non nul. Plus formellement, on définit le support par : .
- sa hauteur (height en anglais), qui représente le degré maximal d'appartenance à . Formellement, la hauteur est définie par :
.
On définit également la notion de coupe α (α-cut en anglais) comme l'ensemble des éléments de pour lesquels le degré d'appartenance à est supérieur ou égal à . Plus formellement, on écrira : .
La figure 2 ci-contre illustre la notion de coupe-α pour un ensemble flou trapézoïdal.
Nombres flous
L'idée de nombre flou (en) (fuzzy number en anglais) est d'utiliser un ensemble flou pour représenter une construction linguistique telle que : « x est autour de 15 ». Les nombres flous permettent de capturer l'incertitude autour d'une valeur donnée : intuitivement, plus on s'éloigne de la valeur 15, plus l'appartenance à l'ensemble flou correspondant diminue.
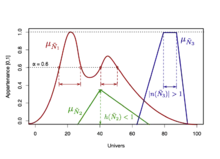
Un nombre flou est un ensemble flou respectant les quatre propriétés suivantes :
- Il est normal, c'est-à-dire que sa hauteur est égale à 1. Plus formellement on écrira : . Sur la figure 3, seuls les nombres et sont normalisés.
- Son noyau est unique, c'est-à-dire qu'il n'existe qu'un seul élément de l'univers pour lequel le degré d'appartenance est égal à 1. Formellement, on écrira : . Cet élément unique est le mode de et est parfois dénoté par le symbole . Sur la figure 3 par exemple, le noyau de l'ensemble flou est unique alors que celui de ne l'est pas.
- Il est convexe, c'est-à-dire qu'il n'existe pas de coupe-alpha disjointe. Formellement la convexité d'un ensemble flou vérifie que : . Sur la figure 3 par exemple, l'ensemble flou n'est pas convexe, car il existe des coupes alpha qui sont discontinues, alors que et le sont.
- Sa fonction d'appartenance, , est continue.
Arithmétique floue théorique
Introduction par l'exemple
Intuitivement, ajouter, soustraire, multiplier ou diviser deux nombres flous nécessite de calculer la fonction d'appartenance associée au résultat (un autre nombre flou). À titre d'exemple, on s'intéresse ici à l'expression arithmétique où et sont deux nombres flous, dont les fonctions d'appartenances sont illustrées sur la figure 4 ci-contre. Leurs fonctions d'appartenance sont respectivement définies par :

Pour calculer le degré d'appartenance de 18 à l'ensemble flou , il est nécessaire de construire tous les couples de valeurs tels que , et où . En effet, cinq couples voient leur somme égale à 18 et tous peuvent donc être à l'origine de ce résultat. De manière logique, on peut donc écrire :
En appliquant la sémantique des opérateurs standards de la logique floue[3], on obtient :

Le tableau de la figure 5 ci-contre résume le calcul pas-à-pas de la fonction d'appartenance de .
Principe général
Dans le cas général, la fonction d'appartenance qui caractérise le résultat d'une opération définie par et appliquée à nombres flous est définie par le produit de convolution max-min tel que :
Il s'agit en fait d'appliquer le principe d'extension de la logique floue, qui permet de calculer le degré d'appartenance d'une relation portant sur des ensembles flous. Bien que cette définition ne permette pas déduire analytiquement l'équation exacte des fonctions d'appartenance résultant d'opérations arithmétiques, elle pose cependant les bases nécessaires à la mise en œuvre de l'arithmétique floue (voir la section sur les arithmétiques floues concrètes et notamment le paragraphe concernant l'utilisation de nombres flous décomposés qui est considérée comme la mise en œuvre standard).
Le tableau ci-dessous résume les principales propriétés des opérations de base de l'arithmétique floue. L'arithmétique floue est en fait une généralisation de l'arithmétique des intervalles (voir arithmétique de nombres flous décomposés).
| Addition | Soustraction | Multiplication | Division | |
|---|---|---|---|---|
| Commutativité | Oui | Oui | ||
| Associativité | Oui | Oui | ||
| Distributivité | Oui (sur + et -) | Oui (sur + et -) | ||
| Élément neutre | Singleton 0 | Singleton 0 | Singleton 1 | Singleton 1 |
| Élément absorbant | Singleton 0 |
Déconvolutions et opérations inverses
Contrairement à l'arithmétique sur les réels, la soustraction définie par l'arithmétique floue n'est pas l'inverse de l'addition, de même que la division n'est pas l'opération inverse de la multiplication.
La figure 6 ci-contre illustre la différence entre l'opération inverse de l'addition et la soustraction : est la somme des nombres et . On peut voir que l'opération génère un quatrième nombre flou () différent de . Si et partage le même mode, l'incertitude autour de est beaucoup plus large. Dans le cadre de l'arithmétique floue, la soustraction et l'opération inverse de l'addition ne répondent pas à la même question:
- la soustraction exprime l'incertitude autour du résultat de l'opération ( sur la figure 6).
- l'opération inverse de l'addition exprime l'incertitude maximale qui, ajoutée à celle de , produit le nombre (Le nombre sur la figure 6).
Arithmétiques floues concrètes
L'étude des opérations arithmétiques appliquées aux nombres flous a abouti à différentes représentations des nombres flous : les nombres flous gauche/droite tout d'abord, puis les nombres flous discrétisés et finalement les nombres flous décomposés, qui sont aujourd'hui l'implémentation de référence. Les paragraphes suivants en donnent un bref aperçu.
Arithmétique des nombres flous G/D
Les nombres flous "gauche/droite", (GD en abrégé ou LR en anglais), ont été l'une des premières implémentations proposées des nombres flous, due notamment à Dubois et Prade. L'idée est de représenter un nombre flou par son support et par son noyau, ainsi que par la forme générale de sa fonction d'appartenance, sous la forme d'un triplet (g, n, d) où g et d représentent respectivement les bornes gauche et droite de la fonction d'appartenance, et où n représente son noyau. Il en résulte différentes familles de nombres flous GD, dont les principales forment les nombres flous triangulaires (nft), gaussiens (nfg), exponentiels (nfe), et quadratiques (nfq), illustrés sur la figure X ci-contre.
L'arithmétique des nombres flous gauches droites se résume alors à application directe des opérations arithmétiques sur les supports et les noyaux, en considérant que les différents familles de nombres flous incompatibles entre elles. La figure 8 illustre l'addition de deux nombres flous triangulaires, A = nft(3, 6, 7) et B = nft(1, 2, 4), qui aboutit au nombre flou C = nft(4, 8, 11).
La principale limitation des nombres flous G/D est leur imprécision. Ils sont avant tout une approximation, certes très rapide à calculer, mais l'erreur induite alors s'amplifie très rapidement, à mesure que les opérations s'enchaînent.
Arithmétique des nombres flous discrets
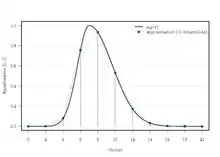
Dans le cas général, la convolution max-min n'a pas de solution analytique, et il est alors nécessaire de se ramener à un espace discret pour pouvoir l'appliquer comme nous l'avons fait sur . L'idée est de réduire la fonction d'appartenance à un nombre limité d'échantillons : plus on conserve d'échantillons, plus l'approximation correspondante est fidèle à la fonction d'appartenance initiale. La figure 7 ci-contre, illustre l'échantillonnage d'un nombre flou.
La principale limite de l'échantillonnage est qu'il ne permet pas de capturer systématiquement le noyau des ensembles flous, et aboutit parfois à des approximations non normalisées. Sur la figure 7 par exemple, le noyau n'est pas échantillonné, et l'approximation correspondante ne satisfait donc pas les propriétés de base des ensembles flous. De plus, du point de vue technique, les techniques de calcul associées sont coûteuses en ressources pour des univers de grande taille, échantillonnés avec une fréquence élevée.
Arithmétique des nombres flous décomposés
L'idée des nombres flous décomposés est de représenter un nombre flou par l'ensemble de ses coupes-α. Pour mémoire, chaque coupe-α représente l'intervalle des valeurs dont le degré d'appartenance est supérieur ou égal à α. L'arithmétique floue se réduit alors à l'arithmétique des intervalles appliquée à différents degrés d'appartenance.
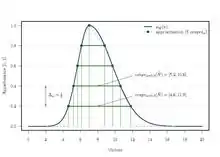
Tout comme un nombre flou discrétisé, un nombre flou décomposé est une représentation discrète de sa fonction d'appartenance. La différence repose sur le choix des échantillons conservés: un nombre flou discrétisé est obtenu en échantillonnant l'univers alors qu'un nombre flou décomposé est obtenu en échantillonnant le domaine des degrés d'appartenance . Étant donné un facteur de décomposition , on divise donc l'intervalle [0,1] en parties de longueur , et on représente par l'ensemble de ses coupes-α où (pour . La figure 8 ci-contre illustre une décomposition en un ensemble de 5 coupes-α. Par opposition à la discrétisation illustrée précédemment sur la figure 7, la décomposition offre l'avantage de capturer systématiquement le noyau des ensembles flous, assurant une représentation cohérente, même pour les singletons.
En représentant les coupes-α correspondantes sous la forme d'intervalles, l'arithmétique floue se réduit à l'arithmétique des intervalles. Par conséquent, pour un degré d'appartenance donné α, la coupe-α caractérisant le résultat d'une opération arithmétique sur et se calcule en appliquant cette même opération sur les intervalles représentant les coupes-α de A et de B. Plus formellement, pour tout et pour tout , on a :
Brève histoire de l'arithmétique floue
Depuis la publication en 1965 des travaux pionniers de L. Zadeh sur les sous ensembles flous[4], de nombreux « systèmes flous » émergent durant les deux décennies suivantes : logique floue, contrôle flou, systèmes experts flous, etc. L'engouement général pour l'Intelligence artificielle accompagne ainsi le développement de l'arithmétique floue, qui, bien qu'initialement considérée comme un exercice académique, se concrétise dans les années 1980 avec la notion de nombre flous GD introduit par Dubois et Prade en 1978 [5] et avec les travaux de R. Yager [6] qui précise, en 1986, le principe d'extension initialement du à Zadeh[7]. Viennent ensuite les nombres flous discrétisés initialement proposés par M. Hanss, mais surtout les nombres flous décomposés proposés par Kauftman et Gupta au début des années 90 [8], qui dressent un parallèle entre l'arithmétique floue et l'arithmétique des intervalles.
Voir aussi
Articles connexes
Notes et références
- Bien qu'il n'y ait pas de consensus officiel sur la notation à utiliser pour dénoter des sous-ensembles flous, de nombreux auteurs utilisent une « vague » représentant l'idée du « flou » et d'approximation. Nous reprenons cette notation qui permet de distinguer visuellement un ensemble flou d'un ensemble au sens classique du terme.
- Contrairement à une fonction représentant une densité de probabilité, l'intégrale d'une fonction d'appartenance ne doit pas nécessairement être égale à 1. La logique floue est ici moins contraignante que la théorie des probabilités et permet de capturer des informations parfois redondantes ou conflictuelles.
- Pour mémoire, la logique floue définit la conjonction, comme et la disjonction par
- Zadeh 1965
- Dubois et Prade 1979
- Yager 1986
- Zadeh 1975
- Kaufman et Gupta 1991
Bibliographie
- (en) Michael Hanss, Applied Fuzzy Arithmetic : An Introduction with Engineering Applications, Berlin, Springer-Verlag, , 256 p. (ISBN 978-3-540-24201-7).

- (en) Arnold Kaufman et Madan M. Gupta, An Introduction to Fuzzy Arithmetic : Theory and Applications, New York, Van Nostrand Reinhold Company Inc., , 394 p. (ISBN 0-442-23007-9).

- (en) George J. Klir et Tina A. Folger, Fuzzy Sets, Uncertainty and Information, Singapour, Prentice Hall Inc. (Simon & Schuster Pte Ltd), , 355 p. (ISBN 978-981-30-2697-1).

- (en) Timothy J. Ross, Fuzzy Logic with Engineering Applications, John Wiley & Sons, Ltd., , 2e éd., 652 p. (ISBN 978-0-470-86075-5).

- (en) Lofti A. Zadeh, « Fuzzy Sets », Information and Control, vol. 8, no 3, , p. 338-353
- (en) Lofti A. Zadeh, « The Concept of Linguistic Variable and its Applications to Approximate Reasoning », Information Science, vol. 8, , p. 199-249
- (en) Didier Dubois et Henri Prade, « Fuzzy Real Algebra: Some Results », Fuzzy Sets and Systems, vol. 2, , p. 327-348
- (en) Ronald R. Yager, « A characterization of the extension principle », Fuzzy Sets and Systems, vol. 18, , p. 205–217
- Portail des mathématiques
- Portail de l’informatique