Automate temporisé

Un automate temporisé possède un nombre fini de places ou états. Les transitions entre états sont instantanées. Dans chaque place, le temps peut s’écouler: à tout instant, la valeur d’une horloge x est le temps écoulé depuis la dernière mise à zéro de x. Les transitions entre états sont conditionnées par des contraintes sur les horloges, appelés gardes, et peuvent remettre certaines horloges à zéro. À chaque place est associée une contrainte sur les horloges, appelée invariant[2].

Un exemple

Un automate temporisé[3]^,[2] à deux états.

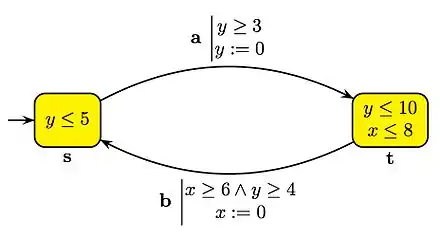
L'automate temporisé ci-contre est composé de deux états ${\displaystyle s}$ et ${\displaystyle t}$. L'état ${\displaystyle s}$est l'état initial. Il y a deux transitions étiquetées respectivement par les lettres d'entrée ${\displaystyle a}$ et ${\displaystyle b}$. L'automate a aussi deux horloges ${\displaystyle x}$ et ${\displaystyle y}$. L'invariant de l'état ${\displaystyle s}$ indique que l'horloge ${\displaystyle y}$ peut valoir au plus 5. Quand elle est au moins égale à 3, la transition vers l'état ${\displaystyle t}$ peut être effectuée. Cette transition entraîne que la réinitialisation de l’horloge ${\displaystyle y}$, i.e. l'horloge ${\displaystyle y}$ est remise à zéro.

L'invariant de l'état ${\displaystyle t}$ porte sur les deux horloges : ${\displaystyle x}$ doit être au plus 8 et ${\displaystyle y}$ au plus 10. La transition vers l'état ${\displaystyle s}$ est possible quand ${\displaystyle x}$est plus grand que 6 et ${\displaystyle y}$ plus grand que 4, et entraîne que la réinitialisation de 'horloge ${\displaystyle x}$ à zéro.

Une trajectoire est une exécution de l'automate. Un automate peut rester dans un état tant que son invariant est satisfait. Il doit quitter l'état avant que l’invariant soit invalide. Pour franchir une transition, il faut que sa garde soit vraie et que l'invariant de l’état d'arrivée soit valide. Voici un exemple d'exécution, où on a séparé la progression du temps dans un état du franchissement de la transition :

${\displaystyle (s,0,0){\xrightarrow[{3}]{}}(s,3,3){\xrightarrow {a}}(t,3,0){\xrightarrow[{4}]{}}(t,7,4){\xrightarrow {b}}(s,0,4){\xrightarrow[{1}]{}}(s,1,5)\cdots }$

Dans cette exécution, la première coordonnée est l'état dans lequel se trouve l'automate temporisée, la deuxième coordonnée est la valeur de l'horloge ${\displaystyle x}$et la troisième coordonnée, celle de l'horloge ${\displaystyle y}$.

On voit aussi l'écriture plus ramassée

${\displaystyle (s,0,0){\xrightarrow[{3}]{a}}(t,3,0){\xrightarrow[{4}]{b}}(s,0,4){\xrightarrow[{1}]{}}(s,1,5)\cdots }$

Voici une autre trajectoire

${\displaystyle (s,0,0){\xrightarrow[{5}]{a}}(t,5,0){\xrightarrow[{3}]{}}(t,8,3)}$.

Ici, l'exécution est bloquée parce que, d'une part l'horloge ${\displaystyle x}$ a atteint 8, qui est la valeur maximale autorisée par l'invariant de l'état ${\displaystyle t}$, et d'autre part la garde de la transition de ${\displaystyle t}$ vers ${\displaystyle s}$, qui demande ${\displaystyle y\geq 4}$, n'est pas vérifiée puisque ${\displaystyle y}$ vaut 3[3].

Formellement, un automate temporisé ${\displaystyle {\mathcal {A}}=(Q,\Sigma ,C,E,q_{0},F)}$ est composé des éléments suivants :

• ${\displaystyle Q}$ : un ensemble fini, dont les éléments sont appelés les états, les nœuds ou les places ;
• ${\displaystyle \Sigma }$ : un ensemble fini appelé l'alphabet ou ensemble d'actions ;
• ${\displaystyle C}$ : un ensemble fini, aussi noté ${\displaystyle X}$, dont les éléments sont appelés les horloges ;
• ${\displaystyle E\subset Q\times \Sigma \times \mathbb {B} (C)\times {\mathfrak {P(C)}}\times Q}$ : un ensemble de transitions ; ici :
  • ${\displaystyle \mathbb {B} (C)}$ est l'ensemble des contraintes booléennes des horloges de ${\displaystyle C}$,
  • ${\displaystyle {\mathfrak {P}}(C)}$ est l'ensemble des parties ${\displaystyle C}$ ;
• ${\displaystyle q_{0}}$ : un élément de ${\displaystyle Q}$ appelé l'état initial. On autorise parfois un ensemble d'états initiaux ${\displaystyle Q_{0}\subset Q}$ ;
• ${\displaystyle F}$ : une partie de ${\displaystyle Q}$ dont les éléments sont appelés les états finals[N 1].

Un élément ${\displaystyle (q,a,g,r,q')}$ de ${\displaystyle E}$ est une transition de l'état ${\displaystyle q}$ à l'état ${\displaystyle q'}$ avec l'action ${\displaystyle a}$, la garde ${\displaystyle g}$ et les horloges de ${\displaystyle r}$ réinitialisées.

Une horloge est une variable à valeurs réelles positives ou nulles. Une contrainte d'horloge est de l'une des formes ${\displaystyle x<c}$,${\displaystyle x\leq c}$, ${\displaystyle x>c}$ ou ${\displaystyle x\geq c}$, où ${\displaystyle x}$ est une horloge et ${\displaystyle c}$ est une constante rationnelle. Un ensemble de contraintes est une conjonction d'un ensemble fini de contraintes.

On peut définir des classes d'automates temporisés déterministe ou non déterministes, et comparer les conditions d'acceptation de Büchi ou de Muller. Les langages acceptés par des automates temporisés non déterministes sont fermés pour l'union et l'intersection, mais pas par complémentation ; au contraire, les langages acceptés par des automates temporisés de Muller sont fermés pour toutes les opérations booléennes. Il existe un algorithme de complexité pour tester si le langage d'un automate temporisé non déterministe est vide, en espace polynomial. D'ailleurs, ce problème est PSPACE-complet[1]. Le problème de l'accessibilité est décidable pour les automates temporisés[1]. Des extensions ont été largement étudiées.

Le problème d'universalité (savoir si tous les mots sont acceptés par un automate temporisé non-déterministe) est indécidable. Il est décidable lorsqu'il n'y a qu'une seule horloge, bien que non primitif récursif[4].

Il existe une variété de outils de recherche pour la saisie et l'analyse d'automates temporisés et de leurs extensions, parmi lesquels les model checkers  UPPAAL, Kronos, et l'analyseur d'ordonnancement TIMES.

Les automates temporisées ont été étendues avec des coûts[5]. On indique dans chaque état, le coût de rester dans cet état par unité de temps ; et pour chaque transition, on indique le coût de prendre cette transition. Aini, on peut associer un coût global à une exécution en sommant les coûts des délais dans chaque état et les coûts des transitions prises.

Articles

• Rajeev Alur et David L. Dill, « A Theory of Timed Automata », Theoretical Computer Science, vol. 126, n^o 2,‎ avril 1994, p. 183-235 (lire en ligne) — Article premier

• Rajeev Alur, « Timed Automata », dans N. Halbwachs et D. Peled (éditeurs), Computer Aided Verification, 11th International Conference, CAV '99, Proceedings, Springer, coll. « Lecture Notes in Computer Science » (n^o 1633), 1999 (ISBN 3-540-66202-2, lire en ligne), p. 8-22

Cours

• Olivier Bournez, « Automates temporisés », Cours du DEA Model Checking, École polytechnique, Paris.
• Bruno Denis, « Introduction aux automates temporisés », sur lurpa, ENS Cachan (consulté le 10 octobre 2016).

• Automate fini
• Automate sur les mots infinis
• Automate de Büchi
• Vérification de modèles

• Portail de l'informatique théorique