Autostabilisation

L'autostabilisation, ou auto-stabilisation, est la propriété d'un système réparti, composé de plusieurs machines capables de communiquer entre elles, qui consiste, lorsque le système est mal initialisé ou perturbé, à retourner automatiquement à un fonctionnement correct en un nombre fini d'étapes de calcul. Elle a été définie par Edsger Dijkstra en 1974. Essentiellement analysée en informatique théorique, l'autostabilisation vise des applications dans les domaines où l'intervention d'un humain pour rétablir le système après une défaillance est impossible ou dans lesquels il est préférable de s'en passer : les réseaux informatiques, les réseaux de capteurs et les systèmes critiques, tels que les satellites.

Application possible : les réseaux de capteurs
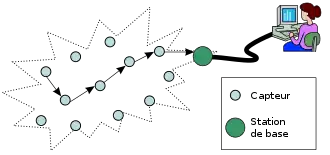
Schéma de principe d'un réseau de capteurs.

Un réseau de capteurs sans fil[1] est un ensemble de petites machines autonomes, les capteurs. Chaque capteur possède un microprocesseur, une petite quantité de mémoire vive, une batterie, un émetteur-récepteur de radio et un ou plusieurs instruments de mesure : thermomètre, hygromètre, etc. Le but d'un tel réseau est de rassembler automatiquement les mesures effectuées par les capteurs individuels pour en déduire un résultat global. Parmi les applications, les réseaux de capteurs peuvent être déployés dans une forêt pour avertir en cas d'incendie[2], dans une zone de conflit pour détecter la présence d'ennemis[3],[4], ou dans un biotope afin d'observer des animaux sans les perturber[5]. Les capteurs étant limités à des processeurs rudimentaires, leur puissance de calcul est limitée. De plus, leurs batteries sont réduites et la consommation en énergie augmente avec la portée des transmissions radio, ce qui limite la distance de leurs communications. En effet, comme les capteurs sont surtout utilisés dans les endroits difficiles d'accès, il n'est généralement pas prévu d'intervenir sur eux pour remplacer la batterie. En général, l'information en provenance des capteurs est récupérée par une station de base (schéma ci-contre) qui possède une plus grande puissance de calcul et de transmission. En règle générale, les capteurs sont fixes : on les pose à un endroit donné et ils ne peuvent pas se déplacer.

Un réseau de capteurs, pour être utile, doit être autonome. Les capteurs doivent s'échanger leurs informations et effectuer leurs traitements sans jamais nécessiter d'intervention. Or, de nombreuses perturbations du système peuvent se produire. Par exemple, un capteur peut tomber en panne, ou de nouveaux capteurs peuvent être déployés dans la zone. L'autostabilisation est une des solutions permettant de s'assurer que le réseau de capteurs récupère automatiquement de ces perturbations[6].

Capteurs Sun SPOT.

Des algorithmes autostabilisants peuvent résoudre les problèmes de base spécifiques aux réseaux de capteurs, en particulier le multiplexage temporel[7] (les capteurs s'accordent sur des créneaux pendant lesquels un seul d'entre eux émet), la communication par diffusion orientée[8] (une méthode de routage adaptée aux réseaux de capteurs[9]), et le fonctionnement en dépit du fait que certains capteurs peuvent être périodiquement coupés du reste du réseau[10]. De même, des solutions autostabilisantes adaptées aux réseaux de capteurs existent pour des problèmes classiques tels que la coloration de graphe[11], le calcul d'un stable maximum[11] ou d'un arbre couvrant[11], ou encore la synchronisation d'horloges[12].

Il existe également des réseaux de capteurs mobiles, dans lesquels les capteurs sont posés sur des agents capables de se déplacer. Ceci donne une nouvelle façon d'observer des animaux sauvages sans perturber leur comportement[13],[14] en installant les capteurs non plus dans le biotope, mais sur les animaux eux-mêmes. Les conditions nécessaires et suffisantes pour résoudre le problème du comptage autostabilisant, qui consiste à déterminer le nombre de capteurs présents dans le système, ont été établies dans ce cadre[15],[16]. Cette problématique rejoint celle des protocoles de populations, qui avait été formulée séparément, et qui consiste à considérer le système comme un ensemble d'agents à mémoire très limitée qui se déplacent aléatoirement, capables de s'échanger des informations lorsqu'ils se rencontrent[17].

Définitions

L'autostabilisation est définie dans le formalisme de l'algorithmique répartie, dont elle est une branche. Les définitions ci-dessous se limitent à ce qui est nécessaire pour caractériser l'autostabilisation.

Modèle

Un système[D 1] est un ensemble de n processus. Chaque processus possède des variables dans lesquelles sont enregistrées les informations que possède le processus. La collection des variables d'un processus est son état.

Deux modèles existent pour représenter les communications entre processus. Le premier modèle est à passage de messages : les processus peuvent communiquer en s'envoyant des messages via des canaux FIFO. Dans ce cas, l'existence ou non d'un canal entre deux processus donnés est définie par la topologie du réseau. L'état d'un canal est défini comme la séquence des messages qu'il contient. Le deuxième modèle est à mémoire partagée. Dans ce cas, il existe un certain nombre de registres partagés et il faut définir quels processus peuvent lire et écrire dans quels registres. L'état d'un registre est la valeur qu'il contient. La configuration du système est la collection de l'état de tous les processus et moyens de communication.

Principe de l'autostabilisation : le système, initialisé dans une configuration quelconque, finit par atteindre une configuration sûre. Toutes les configurations par lesquelles il passe ensuite sont sûres.

Un pas c→c' du système est défini comme l'exécution d'une transition par un processus tel que le système est au départ dans la configuration c, puis, en exécutant une action, passe dans la configuration c'. Au cours d'une transition, un processus peut recevoir un message (resp. lire un registre partagé dans le cas d'un modèle à mémoire partagée), changer d'état, et envoyer des messages (resp. écrire dans des registres partagés).

Une exécution est une suite alternée infinie de configurations et de pas : E = (c0,a1,c1,a2,c2,…) tel que pour tout i > 0, l'action ai fait passer le système de la configuration ci-1 à la configuration ci. Elle est dite équitable si elle ne contient pas de séquence infinie de pas au cours de laquelle une certaine transition pourrait être exécutée, mais ne l'est jamais. En d'autres termes, dans une exécution équitable, aucun processus n'est privé de la possibilité d'effectuer une certaine transition.

Autostabilisation

Pour tout système autostabilisant, on définit un ensemble ℒ d'exécutions légitimes. Cet ensemble représente les exécutions dans lesquelles le système se comporte toujours correctement. Une configuration c est dite sûre vis-à-vis de ℒ si et seulement si toute exécution commençant par c est dans ℒ. Un système est autostabilisant vers ℒ si et seulement si toute exécution de ce système, quelle que soit la configuration de départ, atteint une configuration sûre vis-à-vis de ℒ[D 2].

Propriété fondamentale

Un système est autostabilisant si et seulement si on peut associer à toute configuration une valeur prise dans un anneau noethérien tel que tout pas de l'exécution commençant dans une configuration non sûre de valeur v fait passer le système dans une configuration de valeur v'<v, et les valeurs les plus basses de l'anneau correspondent aux configurations sûres[D 3]. Cette propriété, démontrée par Gouda[18], est utilisable pour démontrer qu'un algorithme est autostabilisant, de la même façon qu'elle peut servir à démontrer qu'un algorithme séquentiel s'arrête.

Mesures de complexité

La mesure de l'efficacité d'un algorithme est l'objet de la l'analyse de la complexité des algorithmes. Elle définit des méthodes permettant de calculer les performances d'un algorithme, principalement selon deux axes : le temps de calcul et la quantité de mémoire utilisée[19]. Dans le cas de l'autostabilisation, on définit le temps de stabilisation comme le temps le plus élevé que le système peut mettre à atteindre une configuration sûre. Dans un système asynchrone, qui ne dispose pas de notion de temps, on définit une ronde comme la plus courte séquence de pas de l'exécution au cours de laquelle chaque processus est activé au moins une fois, ce qui donne une unité dans laquelle on peut exprimer un temps de stabilisation[D 2]. Les autres mesures de complexité définies dans les systèmes répartis s'appliquent aussi en autostabilisation : on peut ainsi chercher à échanger le moins possible de messages ou à utiliser un minimum de mémoire sur chaque processus[D 4].

Interprétation en pratique

À la suite de tout incident qui change l'état du système, l'autostabilisation assure de retrouver automatiquement, après un certain temps de fonctionnement sans nouvel incident, une exécution légitime, et donc un fonctionnement correct. En particulier, cela permet de tolérer toute défaillance transitoire, modification arbitraire de l'état d'un processus au cours d'une exécution. Une telle défaillance peut être causée, par exemple, par un rayon cosmique frappant un circuit intégré[20]. Elle peut aussi être due au fonctionnement du système dans de mauvaises conditions, en particulier en cas de surchauffe ou de surcadencement. Une défaillance transitoire laisse le système dans une configuration quelconque, totalement imprévisible. Ce retour automatique à la normale est particulièrement souhaitable dans un système sur lequel il n'est pas possible de faire intervenir un technicien[D 5], par exemple un satellite.

Dans la plupart des systèmes informatiques, le programme lui-même est une donnée enregistrée en mémoire vive. En conséquence, il est sujet aux défaillances transitoires, ce qui empêche l'autostabilisation. La solution est d'enregistrer le programme en mémoire morte. Si le programme doit être chargé en mémoire vive, un chien de garde[21] peut le recharger à partir de la ROM en cas de besoin. Une autre possibilité est de réaliser directement le programme sous forme de circuit intégré.

Anneau à jeton de Dijkstra et historique
Edsger Dijkstra.

Le concept d'autostabilisation est formulé pour la première fois par Dijkstra en 1974[note 1] dans un article[22] qui présente trois algorithmes autostabilisants basés sur le concept d'anneau à jeton. Le principe de l'anneau à jeton est de résoudre le problème de l'exclusion mutuelle en faisant circuler un jeton, qui représente le droit pour le seul processus qui le possède d'effectuer une action qui poserait problème si plusieurs processus l'effectuaient en même temps, par exemple envoyer du texte à une imprimante[23] : un processus qui veut imprimer doit d'abord attendre de recevoir le jeton, puis envoyer son texte à l'imprimante ; après quoi, il perd le jeton. Dans le cas d'un anneau à jeton autostabilisant, si le système est perturbé par l'introduction d'un ou plusieurs jetons supplémentaires, il récupère de lui-même de cette défaillance en supprimant tous les jetons présents sur l'anneau, sauf un ; puis il poursuit son exécution en passant l'unique jeton restant comme s'il n'y en avait jamais eu d'autre.

Les n processus (avec n impair), numérotés de 0 à n-1, sont reliés en anneau, c'est-à-dire que le processus i a comme voisin de droite i+1 modulo n et comme voisin de gauche i-1 modulo n. Autrement dit, le voisin de gauche du processus 0 est le processus n-1 et le voisin de droite du processus n-1 est le processus 0. Chaque processus a un état entier compris entre 0 et 2. On note É l'état d'un processus, D l'état de son voisin de droite et G celui de son voisin de gauche.

L'algorithme présenté ci-dessous est le troisième de l'article, que Dijkstra considère comme le plus abouti[22]. Une exécution sans défaillance est donnée pour montrer comment se comporte normalement le système, puis le problème de la suppression des privilèges surnuméraires est abordé.

Fonctionnement avec un unique privilège
Configuration initiale (1) : seul le processus 0, en rouge, a un privilège.

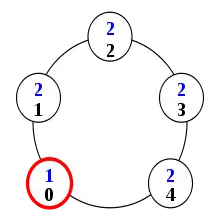
À chaque pas de l'exécution, un processus est choisi arbitrairement par un ordonnanceur. En pratique, cet ordonnanceur dépend du matériel, du système d'exploitation et de l'environnement dans lequel il fonctionne ; son comportement est donc imprévisible. Le côté arbitraire de ce choix est à la base de la motivation initiale de Dijkstra, qui cherche à savoir si un système peut se comporter correctement en dépit d'un contrôle réparti. Dans cet algorithme, seuls les processus qui ont un privilège peuvent réagir lorsqu'ils sont choisis, en changeant d'état. Les privilèges et les changements d'état associés sont définis par les règles suivantes :

  1. Pour le processus 0 : si (É+1) mod 3 = D alors É ← (É-1) mod 3
  2. Pour le processus n-1 : si G=D et (G+1) mod 3 ≠ É alors É ← (G+1) mod 3
  3. Pour tous les autres processus :
    • si (É+1) mod 3 = G alors É ← G
    • si (É+1) mod 3 = D alors É ← D

Ici, le privilège représente le fait pour un processus de posséder un jeton. Pour comprendre comment fonctionne cet algorithme lorsqu'il existe un unique privilège, considérons le cas ci-contre. Les numéros de processus sont en noir, les états en bleu. Le processus 0 a un privilège, matérialisé en rouge, en application de la règle 1. En effet, son état est 1 ; en ajoutant 1, on obtient 2, ce qui est l'état de son voisin de droite. En revanche, aucun autre processus n'a de privilège : le processus 4 parce que les états de ses voisins ne sont pas égaux, les autres processus parce qu'aucun processus n'a l'état (2+1) mod 3 = 0.

Lors du premier pas de l'exécution, c'est donc le processus 0 qui change d'état. En application de la règle 1, il prend l'état 1-1 = 0. Ceci donne un privilège au processus 1, qui change donc d'état lors du pas suivant de l'exécution. Celle-ci continue ainsi :

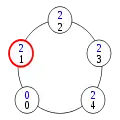  • Configuration (2)
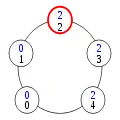  • Configuration (3)
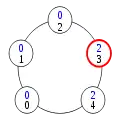  • Configuration (4)
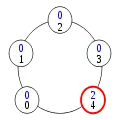  • Configuration (5)

Dans la configuration (5), le processus 4 a le privilège. Il change donc d'état en application de la règle 2, prenant l'état 0+1=1. Ceci donne le privilège au processus 3.

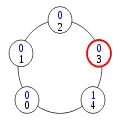  • Configuration (6)
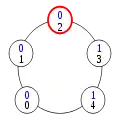  • Configuration (7)
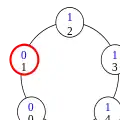  • Configuration (8)
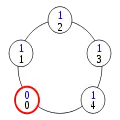  • Configuration (9)

Le privilège a été passé, de proche en proche, à tous les processus. La configuration (9) est équivalente à la configuration (1) ; le système est donc prêt à recommencer à passer le privilège selon le même principe. Le constat que « tout se passe bien » montre, informellement, que cette exécution est légitime.

Fonctionnement avec plusieurs privilèges

Pour comprendre comment l'algorithme garantit que le nombre de privilèges atteint forcément 1, il faut d'abord remarquer que les règles ne permettent aucune situation où il n'existerait pas de privilège. En effet, en vertu de la règle 3, dans une telle configuration, les processus dont les numéros vont de 1 à n-2 doivent tous avoir le même état e ; de plus, les processus 0 et n-1 doivent avoir soit l'état e, soit l'état (e-1) mod 3. Or, si le processus 0 a l'état (e-1) mod 3, alors il a un privilège ; si le processus n-1 a l'état (e-1) mod 3, alors il a un privilège.

La preuve de correction de cet algorithme, publiée en 1986[24], s'appuie sur le fait que si plusieurs privilèges existent, alors leur nombre doit nécessairement diminuer. Pour cela, Dijkstra démontre qu'entre deux changements d'état du processus n-1, il se produit forcément un changement d'état du processus 0. Il prouve ensuite qu'il n'existe pas de séquence de pas infinie dans laquelle le processus 0 ne change pas d'état. Enfin, il établit la liste des scénarios possibles pour le comportement du privilège situé le plus à gauche sur l'anneau et démontre que ce privilège disparaît. Par récurrence, après un certain nombre de pas, il ne reste finalement qu'un seul privilège.

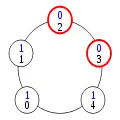  • Premier cas de collision
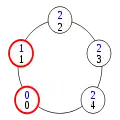  • Deuxième cas de collision

Pour voir comment les privilèges surnuméraires disparaissent, il suffit de constater, dans l'exécution normale ci-dessus, que les privilèges circulent de la gauche vers la droite à partir du processus 0 et de la droite vers la gauche à partir du processus n-1. En conséquence, s'il y a deux privilèges sur l'anneau, ils finissent par se rencontrer. Cette situation est illustrée ci-dessus par le premier cas de collision, où ni le processus 0, ni le processus n-1 n'est impliqué. Dans ce cas, dès que l'un des processus privilégiés change d'état, il perd son privilège alors que l'autre processus garde le sien : le nombre de privilèges a diminué de 1.

Le cas de la collision des processus 0 et 1 est particulier (deuxième cas de collision ci-dessus). En effet, si 1 change d'état, son privilège change simplement de « sens », allant désormais de la gauche vers la droite. Cependant, il peut franchir le processus n-1 et doit donc disparaître. Si c'est le processus 0 qui change d'état, de façon analogue, son privilège passe au processus n-1.

Dijkstra n'aborde pas la question du temps de stabilisation de son algorithme, ni dans son article original de 1974[22], ni dans l'article de 1986 dans lequel il donne la preuve de correction[24]. En 2007, une équipe sans lien avec Dijkstra démontre que cet algorithme se stabilise en O(n²) étapes[25].

Nouvel élan
Leslie Lamport.

Bien que l'algorithme présenté ci-dessus ait été utilisé en production[22], l'article de Dijkstra passe presque inaperçu jusqu'à ce que Leslie Lamport, invité en 1984 à donner une présentation à la conférence PODC, le mentionne comme particulièrement digne d'intérêt[26]. L'autostabilisation devient alors un sujet à part entière en algorithmique répartie, ce que Lamport considère comme une de ses contributions les plus importantes à l'informatique[note 2]. Des étudiants soutiennent des thèses de doctorat sur l'autostabilisation et se spécialisent dans la recherche sur ce sujet[T 1],[T 2],[T 3],[T 4]. L'autostabilisation est enseignée à l'université dans le cadre de cours sur l'algorithmique répartie[27],[28].

En 2000 sort Self-Stabilization, un livre écrit par Shlomi Dolev, le premier entièrement consacré à l'autostabilisation. Par la suite, plusieurs manuels d'algorithmique répartie[29],[30] et de programmation[31] consacrent un chapitre à ce sujet. Dijkstra reçoit le prix PODC de l'article influent pour son article de 1974[32] en 2002, peu avant sa mort. Dès l'année suivante, ce prix est renommé prix Dijkstra en sa mémoire.

Une rencontre internationale sur le thème de l'autostabilisation[33] est lancée en 1989 sous le nom de WSS, Workshop on Self-Stabilizing Systems (« Atelier sur les systèmes autostabilisants »). En 2003, après cinq éditions de l'atelier, la rencontre devient une conférence internationale renommée SSS, Symposium on Self-Stabilizing Systems[34]. En 2005, la conférence élargit son sujet et devient Symposium on Stabilization, Safety, and Security of Distributed Systems (« Congrès sur la stabilisation, la sûreté et la sécurité des systèmes répartis »)[35]. Depuis l'édition de 2003, les actes sont publiés sous forme de livres.

Construction de systèmes autostabilisants

Des travaux de recherche sur l'autostabilisation permettent de mieux comprendre comment il est possible de construire un algorithme autostabilisant. Il est possible de l'obtenir automatiquement à partir d'un algorithme réparti classique au moyen d'un stabilisateur, ou en composant plusieurs algorithmes eux-mêmes autostabilisants. D'autre part, l'analyse de la question du fonctionnement à bas niveau montre les conditions que le matériel doit remplir pour permettre à l'autostabilisation de fonctionner.

Utilisation d'un stabilisateur

Un stabilisateur est un algorithme qui rend autostabilisant n'importe quel algorithme réparti[D 6]. La meilleure solution connue pour réaliser un stabilisateur consiste à donner à un processus distingué le rôle d'examiner tout le système, ce qui suppose d'obtenir et enregistrer l'état de tous les autres processus, puis, si nécessaire, remettre le système à zéro de façon autostabilisante. Cette méthode est trop coûteuse en mémoire et en nombre de messages échangés pour être viable en pratique[36].

Composition équitable
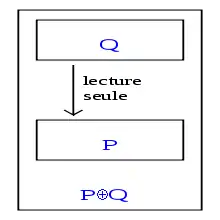
Composition équitable des algorithmes P et Q.

La réutilisation d'algorithmes est une question classique en génie logiciel. Dans le cadre de l'autostabilisation, elle se pose en ces termes : en supposant donnés des algorithmes autostabilisants, est-il possible de les combiner pour obtenir un algorithme global, ou faut-il à chaque fois tout réécrire depuis le début ? La composition équitable[D 7] apporte la réponse : sous certaines conditions, la réutilisation d'algorithmes autostabilisants est possible.

Introduite par Shlomi Dolev, Amos Israeli et Shlomo Moran en 1989[37] et développée par les mêmes auteurs en 1993[38], elle repose sur deux observations. Premièrement, un algorithme Q qui n'écrit pas dans les variables que lit un algorithme P ne peut pas le gêner pour se stabiliser. Deuxièmement, puisque P est autostabilisant, Q peut lire les variables de P pendant sa propre stabilisation : en effet, il est garanti par définition que les valeurs de ces variables finissent par devenir correctes ; à partir de ce moment, Q se stabilise normalement.

Il est donc possible de fusionner les algorithmes P et Q, en ajoutant simplement leurs codes et variables, pour former un nouvel algorithme, noté P⊕Q (voir le schéma ci-contre). Ce nouvel algorithme est lui-même autostabilisant, à condition qu'aucun des algorithmes ne puisse bloquer l'autre ; il faut donc exiger que, dans toute exécution du système global, chacun des deux algorithmes effectue un nombre infini de pas. Cette dernière condition garantit l'équité de l'ordonnancement entre les deux algorithmes, d'où le terme de composition équitable.

Il est ainsi possible de concevoir un algorithme autostabilisant de façon modulaire, en le découpant en sous-algorithmes spécialisés à composer pour obtenir l'algorithme final. Si un algorithme a déjà été écrit pour une tâche donnée, on peut le réutiliser. Par exemple[D 8], si on veut faire circuler un jeton sur un système dont la topologie n'est pas en anneau, il suffit de composer l'algorithme de Dijkstra[22] avec un algorithme de construction de topologie d'où on peut extraire un anneau[38].

Conception d'un matériel autostabilisant

Pour qu'un système puisse réellement être autostabilisant, le matériel sur lequel il fonctionne doit être prévu pour cela. En effet, le matériel ou son micrologiciel peut contenir des bugs qui provoquent son plantage[note 3]. Il est donc nécessaire de s'assurer que le microprocesseur ne puisse pas se bloquer en entrant dans un état duquel il ne peut plus sortir. La recherche dans ce domaine a permis d'identifier précisément les conditions à remplir par le microprocesseur[21], les différents composants matériels de base et les logiciels qui les exploitent afin qu'ils permettent l'autostabilisation : le microprocesseur[21], le système d'exploitation[39],[40], les pilotes de périphériques[41] et le système de fichiers[42]. D'une façon générale, il s'agit de s'assurer qu'aucun blocage n'est possible, ni dans un état dont le système ne peut sortir, ni dans un ensemble d'états où il tournerait sans fin en boucle. Un compilateur préservant la stabilisation[43] a été conçu pour permettre d'écrire des programmes tirant parti de ces matériels et logiciels : si on lui fournit un programme autostabilisant, il produit un code machine respectant ce même concept d'évitement des blocages. Un brevet a été déposé sur la base de ces résultats[44].

Variantes de l'autostabilisation

Selon les circonstances et les problèmes posés, l'autostabilisation est parfois considérée comme inutilement contraignante ou, au contraire, insuffisamment forte. C'est là qu'interviennent des variantes, relâchements ou renforcements de la définition de base.

Pseudo-stabilisation

La pseudo-stabilisation, ou pseudo-autostabilisation[D 9], est un relâchement des contraintes de l'autostabilisation. Au lieu d'exiger que toute exécution se termine dans ℒ, on exige que toute exécution réalise une tâche abstraite, c'est-à-dire un prédicat sur le système. Par exemple, pour spécifier l'exclusion mutuelle, on peut exiger que tous les processus du système possèdent un privilège donné infiniment souvent, mais que deux processus ne le possèdent jamais en même temps. Ceci ne permet pas de définir les exécutions légitimes, car elles doivent reposer sur l'état du système ; or, dans la définition d'une tâche abstraite, c'est impossible car on ne sait rien de la façon dont les processus sont réalisés. La pseudo-stabilisation est moins forte et moins contraignante que l'autostabilisation, car tout système autostabilisant est pseudo-stabilisant, mais la réciproque est fausse. Burns, Gouda et Miller, qui ont introduit cette notion en 1993, estiment qu'elle est généralement suffisante en pratique[45].

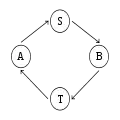  • Première boucle
  • Perte d'un message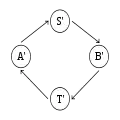
  • Deuxième boucle

L'exemple classique de pseudo-stabilisation[D 10] illustré ci-dessus est un système dans lequel deux processus s'échangent des messages. En fonctionnement normal, le système est dans l'état A ; il envoie un message, ce qui fait passer le système dans l'état S ; l'autre processus reçoit le message, ce qui fait passer le système dans l'état B ; le deuxième processus envoie à son tour un message, ce qui fait passer le système dans l'état T ; le premier processus reçoit le message, et le système est de retour dans l'état A. Le problème est que le canal par lequel passent les messages peut perdre un message, auquel cas le système récupère de cette perte en passant dans l'état A'. La définition de A' est totalement dépendante de la méthode utilisée pour récupérer de la perte du message ; elle est donc inconnue au niveau de la tâche abstraite. À partir de A', l'exécution se poursuit de façon similaire : A', S', B', T', A', etc.

Comme la perte d'un message peut se produire, le système n'est pas autostabilisant vers la boucle A, S, B, T. D'un autre côté, cette perte de message peut très bien ne jamais arriver, ce qui fait que le système n'est pas non plus autostabilisant vers la boucle A', S', B', T', ni vers l'ensemble des états possibles. En revanche, ce système, sans être autostabilisant, est bien pseudo-stabilisant pour la tâche abstraite selon laquelle les deux processeurs s'échangent des messages à tour de rôle, puisque la perte d'un message ne remet pas en cause cette définition.

Superstabilisation

L'idée de la superstabilisation[D 11], introduite par Shlomi Dolev et Ted Herman[46], est de considérer le changement de topologie, c'est-à-dire l'ajout ou le retrait d'un lien de communication dans le système, comme un événement spécial dont tout processus concerné est averti et qui déclenche une procédure appelée section d'interruption. Grâce à cela, le système est capable de garantir qu'une propriété de sûreté particulière, le prédicat de passage, reste toujours vérifiée pendant la stabilisation lorsqu'un changement de topologie se produit à partir d'une configuration sûre. Ceci renforce les garanties données par le système face à un type de défaillance très fréquent en pratique. Plusieurs problèmes de base de l'algorithmique répartie ont été résolus par un algorithme superstabilisant, par exemple l'exclusion mutuelle[47], la construction d'un arbre couvrant[48] et la construction d'un arbre de Steiner[49].

Stabilisation instantanée

Au lieu de laisser le système appliquer son algorithme et se corriger si nécessaire, il est possible de faire l'inverse : surveiller le système en permanence pour chercher les incohérences et les corriger immédiatement, avant de laisser un pas s'effectuer. Ainsi, le système se comporte toujours conformément à sa spécification : il est autostabilisant en zéro étape[50]. Un système instantanément stabilisant résiste donc parfaitement aux défaillances transitoires, sans qu'un observateur ne s'aperçoive qu'elles se sont produites.

Pour le moment, seuls quelques algorithmes basiques instantanément stabilisants ont été développés, par exemple pour le problème du parcours en profondeur d'un réseau identifié quelconque[51] ou la communication point à point dans un réseau commuté[52]. Il est possible de rendre instantanément stabilisant tout algorithme autostabilisant en mémoire partagée, mais la transformation a un coût élevé[53]. Enfin, la stabilisation instantanée est utilisable dans les systèmes à passage de messages, mais là encore, avec un surcoût considérable[54].

Approche probabiliste

Dans une version étendue de son article fondateur[55], Dijkstra établit qu'il ne peut pas exister d'algorithme d'anneau à jeton autostabilisant dans lequel tous les processus sont identiques, à moins que la taille de l'anneau ne soit un nombre premier. En 1990, Ted Herman apporte un moyen de surmonter cette limitation : obliger l'ordonnanceur à se comporter non plus de façon non-déterministe, mais de façon probabiliste[D 4], avec pour preuve de concept l'algorithme d'anneau à jeton autostabilisant probabiliste suivant[56] : le nombre de processus est impair, et l'état de chaque processus est un bit, qui ne peut donc valoir que 0 ou 1. Un processus possède un jeton si et seulement si son état est le même que celui de son voisin de gauche. Dans la configuration (1) ci-dessous, le processus 0 a un jeton car son état est 1, comme pour le processus 4, et aucun autre processus n'a de jeton. Tout processus qui a un jeton est susceptible d'être choisi par l'ordonnanceur pour changer d'état. Dans ce cas, son nouvel état est tiré au sort : 0 ou 1, avec probabilité ½.

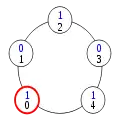  • Configuration (1)
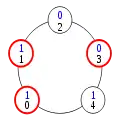  • Configuration (2)

L'interprétation de cette règle en pratique est que le processus a une chance sur deux de garder son jeton, et une chance sur deux de le passer au processus suivant sur l'anneau. Dans la configuration (1), si le processus qui a le jeton tire l'état 1, rien ne change. S'il tire l'état 0, il n'a plus de jeton, car son nouvel état est identique à celui de son voisin de gauche. En revanche, le processus 1 a maintenant un jeton, car il a le même état que son voisin de gauche.

Dans la configuration (2), trois processus ont un jeton. Selon le processus choisi par l'ordonnanceur et le résultat du tirage au sort, après un pas de l'exécution, il peut rester trois jetons ou seulement un. Ainsi, si le processus 1 est choisi, il peut soit garder son jeton, soit le transmettre au processus 2, ce qui ne change pas le nombre de jetons. Mais si le processus 0 est choisi et tire l'état 0, non seulement il perd son jeton, mais le processus 1 perd également le sien. Un ordonnanceur non-déterministe, comme celui utilisé par Dijkstra, pourrait obliger les processus à passer leurs jetons sans jamais les perdre, mais un ordonnanceur probabiliste ne peut pas le faire, car la perte du jeton a une probabilité strictement positive : au cours d'une exécution infinie, elle se produit donc avec probabilité 1.

Dans le cas d'un algorithme probabiliste, il n'est pas possible de calculer un temps de stabilisation, car celui-ci dépend des tirages aléatoires. En revanche, il est possible de calculer son espérance. Initialement, Herman démontre[56] que l'espérance du temps de stabilisation de son algorithme est O(n² log n) étapes. Un calcul plus précis montre par la suite[57] que cette espérance est exactement Θ(n²) étapes. Des recherches plus récentes donnent un cadre général basé sur la théorie des chaînes de Markov pour effectuer ces calculs de complexité dans le modèle probabiliste[58].

Notes et références

Notes
  1. Certains auteurs, par exemple Shlomi Dolev dans son livre Self-Stabilization, parlent d'une précédente parution en 1973, mais elle ne figure sur aucun catalogue officiel. D'autre part, Dijkstra, dans son article de 1986 A Belated Proof of Self-Stabilization, indique qu'il a publié son article fondateur en 1974.
  2. « I regard the resurrection of Dijkstra's brilliant work on self-stabilization to be one of my greatest contributions to computer science. » (« Je considère la résurrection de l'excellent travail de Dijkstra sur l'autostabilisation comme l'une de mes plus grandes contributions à l'informatique »), sur Leslie Lamport, « The Writings of Leslie Lamport » (consulté le )
  3. Exemple pour les processeurs Intel Core 2 : (en) [PDF] « Intel® Core™ 2 Duo Processor E8000Δ and E7000Δ Series — Specification Update », Intel (consulté le )

Références
  1. p. 5-9
  2. p. 9
  3. p. 31
  4. p. 11
  5. p. 1
  6. p. 121
  7. p. 22
  8. p. 24
  9. p. 45
  10. p. 47
  11. p. 159
  • Références à des thèses de doctorat
  1. (en) Ted Herman, Adaptivity through distributed convergence, University of Texas at Austin (thèse de doctorat en informatique),
  2. (en) Shlomi Dolev, Self-Stabilization of Dynamic Systems, Technion, Haïfa (thèse de doctorat en informatique),
  3. (en) George Varghese, Self-stabilization by Local Checking and Correction, University of California, San Diego La Jolla (thèse de doctorat en informatique),
  4. Sébastien Tixeuil, Auto-stabilisation efficace, Université de Paris Sud 11 (thèse de doctorat en informatique), (lire en ligne)
  • Autres références
  1. (en) Holger Karl et Andreas Willig, Protocols and Architectures for Wireless Sensor Networks, WileyBlackwell, , 524 p. (ISBN 978-0-470-51923-3, présentation en ligne)
  2. (en) Liyang Yu, Neng Wang et Xiaoqiao Meng, « Real-time forest fire detection with wireless sensor networks », Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing,‎ , p. 1214 - 1217
  3. Randall Parker, « US Military Sensor Network In Iraq Invasion Performed Poorly », ParaPundit (consulté le )
  4. David Greig, « The soldier helmet that pinpoints enemy snipers », Gizmag (consulté le )
  5. (en) Jean Kumagai, « Life of birds (wireless sensor network for bird study) », IEEE Spectrum, vol. 41, no 4,‎ , p. 42-49
  6. (en) Ted Herman, « Models of Self-Stabilization and Sensor Networks », 5th International Workshop on Distributed Computing,‎ , p. 205-214
  7. (en) Mahesh Arumugam et Sandeep S. Kulkarni, « Self-stabilizing Deterministic TDMA for Sensor Networks », Second International Distributed Conference on Computing and Internet Technology,‎ , p. 69-81 (lire en ligne [PDF])
  8. (en) Doina Bein et Ajoy Kumar Datta, « A Self-Stabilizing Directed Diffusion Protocol for Sensor Networks », ICPP Workshops,‎ , p. 69-76 (lire en ligne [PDF])
  9. (en) Chalermek Intanagonwiwat, Ramesh Govindan et Deborah Estrin, « Directed diffusion: a scalable and robust communication paradigm for sensor networks », MOBICOM,‎ , p. 56-67
  10. (en) Ted Herman, Sriram V. Pemmaraju, Laurence Pilard et Morten Mjelde, « Temporal Partition in Sensor Networks », Proceedings of the 9th International Symposium on Stabilization, Safety, and Security of Distributed Systems,‎ , p. 325-339
  11. (en) Christoph Weyer, Volker Turau, Andreas Lagemann et Jörg Nolte, « Programming Wireless Sensor Networks in a Self-Stabilizing Style », Proceedings of the Third International Conference on Sensor Technologies and Applications,‎
  12. (en) Ted Herman et Chen Zhang, « Best Paper: Stabilizing Clock Synchronization for Wireless Sensor Networks », 8th International Symposium on Stabilization, Safety, and Security of Distributed Systems,‎ , p. 335-349
  13. « The ZebraNet Wildlife Tracker » (consulté le )
  14. (en) Philo Juang, Hidekazu Oki, Yong Wang, Margaret Martonosi, Li-Shiuan Peh et Daniel Rubenstein, « Energy-Efficient Computing for Wildlife Tracking: Design Tradeoffs and Early Experiences with ZebraNet », Proceedings of the Tenth International Conference on Architectural Support for Programming Languages and Operating Systems,‎ (lire en ligne [PDF])
  15. (en) Joffroy Beauquier, Julien Clément, Stéphane Messika, Laurent Rosaz et Brigitte Rozoy, « Self-stabilizing Counting in Mobile Sensor Networks with a Base Station », 21st International Symposium on Distributed Computing,‎ , p. 63-76
  16. (en) Joffroy Beauquier, Julien Clément, Stéphane Messika, Laurent Rosaz et Brigitte Rozoy, « Self-stabilizing Counting in Mobile Sensor Networks with a Base Station », Proceedings of the Twenty-Sixth Annual ACM Symposium on Principles of Distributed Computing,‎ , p. 396-397
  17. (en) Dana Angluin, James Aspnes, Michael J. Fischer et Hong Jiang, « Self-stabilizing population protocols », ACM Transactions on Autonomous and Adaptive Systems, vol. 3, no 4,‎
  18. (en) Mohamed G. Gouda, « The Triumph and Tribulation of System Stabilization », Proceedings of the 9th International Workshop on Distributed Algorithms,‎ , p. 1-18
  19. (en) Christos H. Papadimitriou, Computational Complexity, Addison Wesley, , 523 p. (ISBN 978-0-201-53082-7)
  20. (en) James F. Ziegler, « Terrestrial cosmic rays », IBM Journal of Research and Development, vol. 40, no 1,‎ , p. 19-40
  21. (en) Shlomi Dolev et Yinnon A. Haviv, « Self-Stabilizing Microprocessor: Analyzing and Overcoming Soft Errors », IEEE Transactions on Computers, vol. 55, no 4,‎ , p. 385-399
  22. (en) Edsger Wybe Dijkstra, « Self-stabilizing Systems in Spite of Distributed Control », Communications of the ACM, vol. 17, no 11,‎ , p. 643-644 (lire en ligne [PDF])
  23. (en) Nancy Lynch, Distributed Algorithms, Morgan Kaufmann, , 904 p. (ISBN 978-1-55860-348-6), p.  255
  24. (en) Edsger Wybe Dijkstra, « A belated proof of self-stabilization », Distributed Computing, vol. 1, no 1,‎ , p. 5-6 (lire en ligne [PDF])
  25. (en) Viacheslav Chernoy, Mordechai Shalom et Shmuel Zaks, « On the Performance of Dijkstra's Third Self-stabilizing Algorithm for Mutual Exclusion. », Proceedings of the 9th International Symposium on Stabilization, Safety, and Security of Distributed Systems,‎ , p. 114-123 (lire en ligne [PDF])
  26. (en) Leslie Lamport, « Solved Problems, Unsolved Problems and Non-Problems in Concurrency (invited address) », Principles of Distributed Systems,‎ , p. 1-11 (lire en ligne [PDF])
  27. « Algorithmique répartie et tolérance aux défaillances » [archive du ], Master Parisien de Recherche en Informatique (consulté le )
  28. (en) Vijay Garg, « EE 382N: Distributed Systems Syllabus » (consulté le )
  29. Tel 2001
  30. Garg 2002
  31. Garg 2004
  32. (en) « PODC Influential Paper Award: 2002 », PODC (consulté le )
  33. « Self-Stabilization Home Page » (consulté le )
  34. « Sixth Symposium on Self-Stabilizing Systems » (consulté le )
  35. « Eighth International Symposium on Stabilization, Safety, and Security of Distributed Systems » (consulté le )
  36. (en) Baruch Awerbuch, Shay Kutten, Yishay Mansour, Boaz Patt-Shamir et George Varghese, « Time optimal self-stabilizing synchronization », Proceedings of the twenty-fifth annual ACM symposium on Theory of computing,‎ , p. 652-661
  37. (en) Shlomi Dolev, Amos Israeli et Shlomo Moran, « Self-stabilization of Dynamic Systems », Proceedings of the MCC Workshop on Self-stabilizing Systems,‎
  38. (en) Shlomi Dolev, Amos Israeli et Shlomo Moran, « Self-Stabilization of Dynamic Systems Assuming Only Read/Write Atomicity », Distributed Computing, vol. 7, no 1,‎ , p. 3-16
  39. (en) Shlomi Dolev et Reuven Yagel, « Towards Self-Stabilizing Operating Systems », IEEE Transactions on Software Engeneering, vol. 34, no 4,‎ , p. 564-576
  40. (en) Shlomi Dolev et Reuven Yagel, « Memory Management for Self-stabilizing Operating Systems », Proceedings of the 7th International Symposium on Self-Stabilizing Systems,‎ , p. 113-127
  41. (en) Shlomi Dolev et Reuven Yagel, « Self-stabilizing device drivers », ACM Transactions on Autonomous and Adaptive Systems, vol. 3, no 4,‎
  42. (en) Shlomi Dolev et Ronen Kat, « Self-stabilizing distributed file system », Journal of High Speed Networks, vol. 14, no 2,‎ , p. 135-153
  43. (en) Shlomi Dolev, Yinnon A. Haviv et Mooly Sagiv, « Self-stabilization preserving compiler », ACM Transactions on Programming Languages and Systems, vol. 31, no 6,‎
  44. (en) « Apparatus and methods for stabilization of processors, operating systems and other hardware and/or software configurations » (consulté le )
  45. (en) James E. Burns, Mohamed G. Gouda et Raymond E. Miller, « Stabilization and Pseudo-Stabilization », Distributed Computing, vol. 7, no 1,‎ , p. 35-42
  46. (en) Shlomi Dolev et Ted Herman, « Superstabilizing Protocols for Dynamic Distributed Systems », Chicago Journal of Theoretical Computer Science,‎ (lire en ligne [PDF])
  47. (en) Ted Herman, « SuperStabilizing Mutual Exclusion », Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications,‎ , p. 31-40
  48. (en) Yoshiak Katayama, Toshiyuki Hasegawa et Naohisa Takahashi, « A superstabilizing spanning tree protocol for a link failure », Systems and Computers in Japan, vol. 38, no 14,‎ , p. 41-51
  49. (en) Lélia Blin, Maria Gradinariu Potop-Butucaru et Stéphane Rovedakis, « A Superstabilizing log(n)-Approximation Algorithm for Dynamic Steiner Trees », Proceedings of the 11th International Symposium on Stabilization, Safety, and Security of Distributed Systems,‎ , p. 133-148
  50. (en) Alain Bui, Ajoy Kumar Datta, Franck Petit et Vincent Villain, « State-optimal snap-stabilizing PIF in tree networks », Proceedings of the ICDCS Workshop on Self-stabilizing Systems,‎ , p. 78-85 (lire en ligne [PDF])
  51. (en) Alain Cournier, Stéphane Devismes, Franck Petit et Vincent Villain, « Snap-Stabilizing Depth-First Search on Arbitrary Networks », Computing Journal, vol. 49, no 3,‎ , p. 268-280
  52. (en) Alain Cournier et Swan Dubois, « A snap-stabilizing point-to-point communication protocol in message-switched networks », Proceedings of the 23rd IEEE International Symposium on Parallel and Distributed Processing,‎ , p. 1-11
  53. (en) Alain Cournier, Stéphane Devismes et Vincent Villain, « From Self- to Snap- Stabilization », Proceedings of the 8th International Symposium on Stabilization, Safety, and Security of Distributed Systems,‎ , p. 199-213
  54. (en) Sylvie Delaët, Stéphane Devismes, Mikhail Nesterenko et Sébastien Tixeuil, « Snap-Stabilization in Message-Passing Systems », Proceedings of the 10th International Conference on Distributed Computing and Networking,‎ , p. 281-286
  55. (en) Edsger Wybe Dijkstra, « Self-stabilization in spite of distributed control », Edsger W. Dijkstra, Selected Writings on Computing: A Personal Perspective,‎ , p. 3 (lire en ligne [PDF])
  56. (en) Ted Herman, « Probabilistic Self-Stabilization », Information Processing Letters, vol. 35, no 2,‎ , p. 63-67
  57. (en) Annabelle McIver et Carroll Morgan, « An elementary proof that Herman’s Ring is Θ(n²) », Information Processing Letters, vol. 94, no 2,‎ , p. 79–84
  58. (en) Laurent Fribourg et Stéphane Messika, « Coupling and self-stabilization », Distributed Computing, vol. 18, no 3,‎ , p. 221-232

Annexes

Bibliographie

 : document utilisé comme source pour la rédaction de cet article.

Depuis l'édition de 2003, les actes de la conférence SSS sont publiés sous forme de livres dans la collection Lecture Notes in Computer Science de Springer Verlag. L'autostabilisation est le seul thème de la conférence jusqu'en 2005, l'un des principaux thèmes par la suite.

  • (en) Shing-Tsaan Huang (dir.) et Ted Herman (dir.), Self-Stabilizing Systems : 6th International Symposium, SSS 2003, San Francisco, Ca, USA, June 24-25, 2003 Proceedings, Springer Verlag, , 215 p. (ISBN 978-3-540-40453-8, présentation en ligne)
  • (en) Sébastien Tixeuil (dir.) et Ted Herman (dir.), Self-Stabilizing Systems : 7th International Symposium, SSS 2005, Barcelona, Spain, October 26-27, 2005 (Lecture Notes in Computer Science), Springer Verlag, , 229 p. (ISBN 978-3-540-29814-4)
  • (en) Ajoy Kumar Datta (dir.) et Maria Gradinariu Potop-Butucaru (dir.), Stabilization, Safety, and Security of Distributed Systems : 8th International Symposium, SSS 2006 Dallas, TX, USA, November 17-19, 2006 Proceedings (Lecture Notes in Computer Science), Springer Verlag, , 805 p. (ISBN 978-3-540-49018-0)
  • (en) Toshimitsu Masuzawa (dir.) et Sébastien Tixeuil (dir.), Stabilization, Safety, and Security of Distributed Systems : 9th International Symposium, SSS 2007 Paris, France, November 14-16, 2007 Proceedings (Lecture Notes in Computer Science), Springer Verlag, , 409 p. (ISBN 978-3-540-76626-1)
  • (en) Sandeep Kulkarni (dir.) et André Schiper (dir.), Stabilization, Safety, and Security of Distributed Systems : 10th International Symposium, SSS 2008, Detroit, MI, USA, November 21-23, 2008, Springer Verlag, , 265 p. (ISBN 978-3-540-89334-9)
  • (en) Rachid Guerraoui (dir.) et Franck Petit (dir.), Stabilization, Safety, and Security of Distributed Systems : 11th International Symposium, SSS 2009, Lyon, France, November 3-6, 2009. Proceedings, Springer Verlag, , 805 p. (ISBN 978-3-642-05117-3)

Articles connexes

Liens externes
  • Portail de l’informatique
  • Portail de l'informatique théorique
La version du 23 février 2010 de cet article a été reconnue comme « article de qualité », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.