Bâtons de Napier
Le bâton de Napier, ou réglette de Neper est un abaque facilitant le calcul des produits, quotients, puissances et racines, inventé par le mathématicien écossais John Napier (en français Neper) en 1617.
_03.jpg.webp)
Napier, qui est déjà inventeur des logarithmes qui portent son nom, décrit sa nouvelle invention dans son ouvrage Rhabdologie (du Grec ραβδoς, règle, et λóγoς, étude). Comme pour les logarithmes, son procédé est basé sur la transformation de puissances en produits et de racines en divisions.
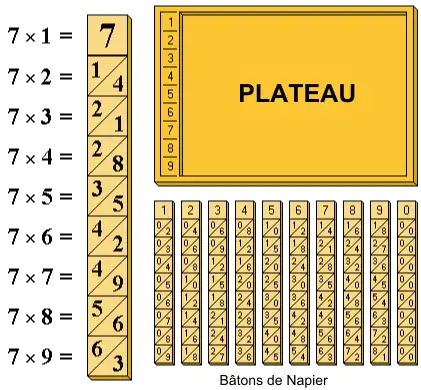
L'abaque est constitué d'un plateau à rebord sur lequel peuvent être placées des réglettes gravées. Le bord gauche du plateau est gravé lui aussi, divisé en neuf cases numérotées de 1 à 9. Les dix types de réglettes, qui ont donné leur nom à l'ensemble du dispositif, étaient originellement en os, d'où le nom anglais de Napier's bones. Elles sont divisées en neuf cases. La case supérieure porte un nombre de 0 à 9. Les huit autres cases sont divisées en deux par un trait diagonal.
Sur chaque réglette est portée la table de multiplication du nombre qui apparaît sur la case supérieure. Ainsi sur la réglette qui débute par le 7, les cases suivantes contiendront 14, 21, 28… jusqu'à 63. Ce sont des nombres à deux chiffres, on fait figurer le chiffre des dizaines et celui des unités de part et d'autre du trait diagonal (voir illustration ci-contre).
Principe de la multiplication et de la division
Multiplication par un nombre inférieur à 10
À titre d'exemple, on effectue le produit de 46 785 399 par 7. Pour cela, on forme le nombre 46 785 399 sur la partie supérieure du tableau. On lit ensuite sur la septième ligne le résultat de la multiplication de chaque chiffre par 7. La disposition obtenue est telle que le résultat se lit directement en additionnant les chiffres qui apparaissent dans les bandes diagonales, de droite à gauche et avec retenues si nécessaire.
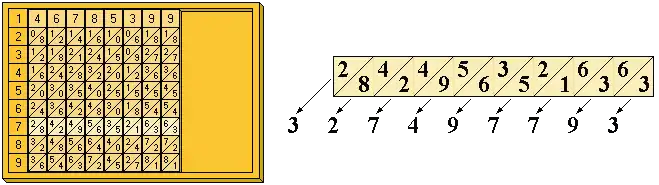
Sur l'exemple on obtient successivement les unités (3), dizaines (6+3=9), centaines (6+1=7), etc.
Multiplication de nombres à plusieurs chiffres
On multiplie cette fois 46 785 399 par 96 431. On trouve facilement par le procédé précédent les produits partiels par 9, 6, 4, 3 et 1. Il reste simplement à les placer de façon adéquate et à les sommer.
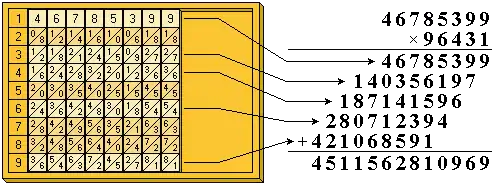
Application à la division
Le fait de disposer d'un algorithme de calcul des produits facilite également la division. On suit la disposition de l'algorithme traditionnel de calcul de la division. Parallèlement, on forme sur la première ligne du plateau la suite des chiffres du diviseur, ce qui permet de lire très rapidement le produit du diviseur par les chiffres de 1 à 9. Il suffit de choisir parmi eux celui qui est immédiatement inférieur au dividende. On calcule alors le reste par soustraction, et on poursuit l'algorithme.
.png.webp)
Bien entendu, cette technique s'applique aussi bien pour déterminer le résultat d'une division entière avec reste, que d'une division à virgule.
Histoire et évolution
Le système des bâtons de Napier est une amélioration de la technique de la multiplication par jalousies (per gelosia).
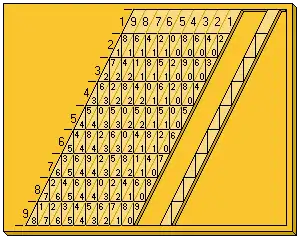
Au cours du XIXe siècle, l'abaque connut une amélioration, avec l'introduction de bâtons inclinés de l'ordre de 65° par rapport au bord du plateau, et dont les cases sont délimitées de façon différente, par des traits parallèles au bord du plateau (voir la figure). L'avantage est de mieux faire apparaître le résultat du produit puisque les cases triangulaires dont il faut ajouter le contenu apparaissent l'une au-dessus de l'autre.
Pour faciliter encore la lecture, les gravures délimitant les cases sont rendues bien visibles, plus que les bords des bâtons. Les produits partiels apparaissent alors très clairement, avec par exemple, sur la figure ci-contre
- 987654321 x 5 = 4938271605
À la fin du XIXe siècle un nouveau procédé est introduit : les réglettes de Genaille-Lucas rendent les calculs de produits plus automatiques en prenant en compte les additions nécessaires lors des produits partiels. Seule reste à effectuer à la main l'addition finale.
Extraction de racine carrée
Description du mode opératoire sur un exemple
L'extraction de racine carrée peut être obtenue de la manière suivante. En ajoutant une baguette spécifique (en jaune sur les figures ci-dessous), il est possible de calculer rapidement des racines carrées. Cette baguette jaune contient les carrés des nombres de 1 à 9.
Soit à calculer la racine carrée de 46 785 399. La méthode utilise fortement les puissances du nombre cent comme il sera expliqué par la suite. Elle s'applique à un nombre ayant un nombre pair de chiffres avant la virgule (au besoin on peut rajouter un zéro avant). Sur l'exemple donné, les étapes sont les suivantes.
- Détermination du premier chiffre de la racine carrée
- isoler les deux premiers chiffres du nombre initial (46, marqués en rouge)
- chercher le chiffre dont le carré précède immédiatement 46 : ici le chiffre 6 ; il constitue le premier chiffre du résultat
- soustraire le carré de 6 à 46 : reste 10, et abaisser deux chiffres suivants du nombre initial. On obtient 1078, nombre avec lequel l'algorithme se poursuit.
- Détermination du second chiffre de la racine carrée
- doubler le premier chiffre de la racine (6 x 2 donne 12), le former sur la première ligne du plateau, et ajouter la baguette jaune à la suite
- parmi tous les nombres qui apparaissent en ligne chercher celui qui précède immédiatement 1078 : ici c'est 1024 dans la ligne 8
- le deuxième chiffre de la racine carrée est donc 8, on forme 1078 - 1024 = 54 et on abaisse deux nouveaux chiffres, l'algorithme se poursuivra avec 5453.
.png.webp)
- Détermination du troisième chiffre de la racine carrée
- doubler le second chiffre de la racine (8 x 2 donne 16), le rajouter au nombre déjà formé multiplié par 10 (12 x 10 + 16 = 136), et ajouter la baguette jaune à la suite
- parmi tous les nombres apparaissant en ligne celui qui précède immédiatement 5453 est 4089, en ligne 3
- le troisième chiffre de la racine carrée est donc 3, on forme 5453 - 4089 = 1364 et on poursuit en abaissant deux chiffres
- ensuite l'algorithme se poursuit : le chiffre suivant est un 9. On peut poursuivre indéfiniment après la virgule, en abaissant des "00" à chaque étape. Mais il faut placer une virgule dans le résultat au moment où on utilise des chiffres après la virgule dans le nombre initial.
Justification
L'idée sous-jacente à l'algorithme est l'utilisation des puissances de 100. Concrètement, cela revient à grouper les chiffres deux par deux, de part et d'autre de la virgule, selon le schéma suivant (en ajoutant, au besoin, un zéro avant le premier chiffre)
- ... xx xx xx xx , xx xx xx ...
Ce qui revient par exemple à écrire
La première étape consiste à casser le premier terme en un carré parfait plus un terme résiduel qui va s'ajouter avec le second terme
À l'issue de la seconde étape on désire aboutir à un résultat de la forme
où a est un chiffre de 0 à 9 et R le plus petit possible. En développant et en refactorisant, on peut mettre cela sous la forme
Justement, le procédé décrit ci-dessus est celui qui permet de trouver a convenable, le plus grand possible, comme le montrent les calculs gravés sur la planche 1. Il n'y a plus qu'à calculer R et à poursuivre.
Voir aussi
Liens externes
- (en) Un abaque en ligne en java fonctionnant dans différentes bases, sur Cut The Knot
- Les bâtons à multiplier, sur culture math
- (it) Simulateur interactif de Bones de Napier
Crédit d'auteurs
- Portail des mathématiques