B-Rep

En infographie, la B-Rep (Boundary Representation en anglais ou Représentation Frontière ou Représentation par les Bords en français[1]) est une technique de modélisation 3D géométrique des solides par les surfaces. Cette méthode consiste à représenter la peau des objets géométriques en « cousant » des carreaux géométriques restreints, portés par des surfaces canoniques (en général des surfaces B-splines, des Bézier, des NURBS).

Exemple de carrosserie construite en modélisation B-Rep. Notez les carreaux surfaciques cousus entre eux. Courtoisie : Ecurie EPSA

Représentation d’un tétraèdre sous forme de BRep

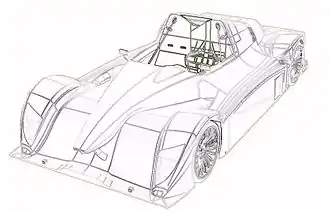
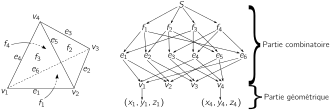
Une B-Rep est un formalisme de représentation dans lequel un solide S est entièrement représenté par son bord[2]: celui-ci est constitué de faces, arêtes et sommets. Une face est une surface orientable et bornée. Une arête est une courbe du bord de S dont les extrémités appartiennent à l’ensemble des sommets. Ces éléments ne doivent pas présenter d’intersection 2 à 2 sauf en des arêtes ou des sommets appartenant au modèle. Les informations combinatoires telles que l’adjacence ou l’incidence sont séparées des informations géométriques telles que la position des sommets, les courbes support des arêtes ou les surfaces support des faces.

Les bases de la B-Rep ont été développées indépendamment au début des années 1970 par Ian Braid (en) de l’Université de Cambridge (pour la vision par ordinateur). Braid a poursuivi ses recherches dans le cadre du modeleur BUILD qui était alors un logiciel pionnier dans ce domaine. Il a également travaillé sur le système commercial ROMULUS, précurseur de Parasolid, et sur ACIS. Ces derniers ont posé les fondements de nombreux systèmes de CAO commerciaux actuels.

Dans le sillage des travaux de Braid, une équipe suédoise dirigée par le professeur Torsten Kjellberg a développé notamment les maillages volumétriques au début des années 1980. En Finlande, Martti Mäntylä a créé le modeleur GWB. Aux États-Unis Eastman et Weiler on également travaillé sur la B-Rep et au Japon le professeur Fumihiko Kimura et son équipe de l’Université de Tokyo ont produit leur propre modeleur B-Rep.

La méthode CSG était utilisée à l’origine par plusieurs systèmes commerciaux car elle est plus facile à implémenter. Avec l’avènement de systèmes tels que Parasolid, ACIS, OpenCASCADE ou encore C3D, B-Rep a commencé à être adopté plus largement.

B-Rep connecte pour l’essentiel des faces, des angles et des points. En groupant des sous-éléments d’une forme on obtient des features, ce qui a été étudié par Kyprianou à Cambridge ainsi que par Jared.

La modélisation géométrique des solides procède de 2 méthodes :

• la B-Rep (dite aussi « modélisation surfacique »),
• la CSG (Constructive Solid Geometry) dite aussi « modélisation solide » ou « modélisation volumique ».

Les modèles B-Rep sont maintenant complétés et étendus. On parle plutôt de modèles cellulaires à formes régulières (simpliciaux, simploïdes, etc.) ou à formes quelconques (graphes d'adjacences, cartes, g-cartes)[3].

Alors que la CSG n’utilise que des primitives simples combinées à l’aide d’opérations booléennes à la B-Rep, la B-Rep est plus flexible et implémente davantage d’opérations. En plus des opérations booléennes, on peut citer entre autres l’extrusion, la création de chanfreins, la fusion de formes et encore d’autres opérations qui dérivent de ces dernières.