Bloc fonctionnel

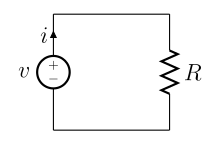
Les modèles par blocs fonctionnels des circuits électroniques reposent sur l’hypothèse simplificatrice que les attributs du circuit : sa résistance, sa capacité, son inductance propre et son facteur de gain, peuvent se ramener à l'interaction de composants électroniques idéaux : résistors, condensateurs, et bobines, etc. connectés entre eux par un réseau de fils parfaitement conducteurs.

La modèle par blocs fonctionnels est convenable tant que ${\displaystyle L_{c}\ll \lambda }$, où ${\displaystyle L_{c}}$ est une dimension caractéristique du circuit, et ${\displaystyle \lambda }$ sa longueur d'onde en fonctionnement.

À défaut, si la taille du circuit est de l'ordre de sa longueur d'onde, il faut envisager des modèles plus généraux, tels les systèmes distribués (dont les lignes de transmission), dont la dynamique est décrite par les équations de Maxwell. Une autre façon de comprendre les limitations inhérentes à la notion de graphe fonctionnel est de voir que ce modèle ne tient pas compte du temps de transfert des signaux d'un bloc à l'autre, et plus globalement du temps de propagation à travers un circuit.

Mais à chaque fois que le temps de propagation est négligeable pour l'application, le modèle par blocs fonctionnels convient. Dans les oscillateurs, c'est le cas lorsque le temps de propagation est nettement inférieur à la période du signal. Si l'on allonge le temps de propagation (par exemple en multipliant les composants intermédiaires), il y aura un déphasage croissant entre le signal réel et les temps d'attente prévus, ce qui se traduira ensuite par une erreur sur l'estimation de l'amplitude du signal. La limite d'utilisation d'un modèle par blocs fonctionnels dépend dans une certaine mesure de la précision avec laquelle on souhaite traiter le signal in fine.

Les composants réels présentent des caractéristiques non linéaires qui résultent, en réalité, de l'interaction d'éléments distribués mais qu'on modélise souvent par une linéarisation, avec des blocs fonctionnels : pour décrire les fuites dans l'isolant d'un condensateur, par exemple, on modélise un condensateur réel comme un condensateur monté en parallèle avec des résistors, bien que les courants de fuites soient distribués spatialement d'une extrémité à l'autre de l'isolant. De même, une résistance à fil enroulé développe inévitablement une certaine inductance distribuée sur toute sa longueur, mais on la modélise par des inductances montées en série avec un résistor idéal.

Les hypothèses simplificatrices sont ici :

• tous les éléments sont des solides rigides;
• les liaisons entre solides sont des accouplements par pivots, ressorts et amortisseurs visqueux.

Dans ce cas, le modèle par blocs fonctionnels repose sur l'approximation des grandeurs distribuées intervenant en l'acoustique théorique. Dans un modèle acoustique, on modélise les propriétés acoustiques de certains composants physiques par des composants électroniques ou des combinaisons simples de ce type de composant.

• On peut modéliser une chambre à parois rigides remplie d'air (ou de tout autre fluide compressible) comme un condensateur dont la capacité serait proportionnelle au volume de la cavité. La validité de cette approximation repose sur le fait que la plus courte longueur d'onde acoustique est très inférieure à la plus grande dimension de la chambre.
• On peut modéliser une enceinte bass-reflex comme une bobine l’inductance serait proportionnelle à la longueur efficace de l’enceinte divisée par sa section droite. La longueur efficace est la longueur géométrique plus une correction, dite « correction de coda ». Cette approximation repose sur le fait que la plus courte longueur d'onde acoustique est beaucoup plus grande que la plus grande dimension de l’enceinte.
• Certains matériaux absorbants peuvent être modélisés comme des résistors. La résistance équivalente dépend des propriétés et des dimensions du bloc absorbeur. Cette approximation dépend des propriétés du matériau et des longueurs d'onde en jeu, qui doivent être suffisamment importantes.
• On peut modéliser un haut-parleur (typiquement un boomer ou un caisson de basse) par un montage en série d'un générateur de tension idéal (c'est-à-dire un générateur d'impédance nulle), une résistance, un condensateur et une bobine (circuit oscillant type RLC). Les paramètres du circuit équivalent dépendent non seulement des caractéristiques techniques du haut-parleur, mais aussi de la longueur d'onde du son émis.

Les hypothèses simplificatrices sont ici :

• tous les mécanismes de transfert thermique sont linéarisés, notamment le rayonnement et la convection ;
• tous les composants (résistors et condensateurs) ont une caractéristique constante sur la durée de simulation, afin que le circuit RC équivalent ait une dynamique linéaire.

Le recours aux modèles par blocs fonctionnels pour représenter les échanges thermiques dans un bâtiment n'offre pas la même précision que les modèles numériques plus récents (par exemple EnergyPlus ou IES <VE>), mais ils sont aussi moins onéreux en temps de calcul. Ainsi, le logiciel de simulation CitySim de D. Robinson, qui se fonde sur un graphe fonctionnel, donne-t-il très rapidement le bilan d'une installation de chauffage : il peut être incorporé dans un algorithme d'analyse stochastique ou un logicielle de simulation urbaine.

Il existe de nombreuses publications décrivant la modélisation fonctionnelle des réseaux de chauffage des bâtiments. Dans la plupart, on modélise le bâtiment comme un casier unique comportant plusieurs blocs (les parois rayonnantes), mais la saisie des propriétés thermiques équivalentes des différentes parois est un véritable calvaire pour l'utilisateur. Pour cette raison, la méthode de Ramallo-González (méthode de la couche dominante) reste la plus simple[1] : elle consiste à choisir, pour chaque fréquence d'étude, l'une des couches comme source principale dans le comportement thermique du bâtiment.

Ce genre de modèles est utilisé pour appréhender l'efficacité des systèmes de chauffage domestique[2].

• Portail des technologies