Blocage de Coulomb
En physique mésoscopique, un blocage de Coulomb (Coulomb Blockade en Ang.), nommé d'après la force électrique de Charles-Augustin de Coulomb, est l'augmentation de la résistance par un faible potentiel appliqué sur un dispositif comprenant au minimum une jonction tunnel de faible capacitance[1].
Le blocage de Coulomb est un mécanisme étudié notamment pour l'élaboration de transistors à un électron (S.E.T. : Single Electron Transistor). Car au travers du blocage de Coulomb, on a la possibilité de contrôler le flux de porteurs, électron par électron.
En raison du blocage de Coulomb, la résistance des dispositifs n'est pas constante à faible potentiel, mais augmente à l'infini pour des potentiels inférieurs à un certain seuil (c.à.d. aucun courant existant). Quand peu d'électrons sont impliqués et un champ magnétique externe et statique est appliqué, le blocage de Coulomb crée des conditions propice pour un blocage de Spin (aussi appelé blocage de Pauli) et un blocage vallée[2],[3] qui inclut les effets de la mécanique quantique dus aux interactions de spin et d'orbite entre les électrons.
Un blocage de Coulomb peut également être observé lors de la création d'un point quantique (Quantum dot en Ang.). Lorsque l'appareil est assez petit, les électrons à l'intérieur de l'appareil créent une forte répulsion coulombienne empêchant les autres électrons de circuler ainsi le dispositif ne suit plus la loi d'Ohm. La relation courant-tension du blocage de coulomb ressemble à un escalier[4].
Dans une jonction tunnel
La jonction tunnel est, dans sa forme la plus simple, une fine barrière isolante entre deux électrodes conductrices. Si les électrodes sont supraconductrices, les paires de Cooper (avec une charge de deux charges élémentaires) transportent le courant. Dans le cas où les électrodes sont des conducteurs normaux, c'est-à-dire ni supraconductrices ni semi-conductrices, les électrons (avec une charge d'une charge élémentaire) transportent le courant. Le raisonnement suivant est celui de jonctions tunnel avec une barrière isolante entre deux électrodes conductrices normales (jonctions NIN).
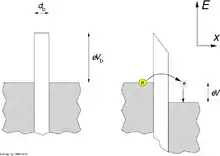
Selon les lois de l'électrodynamique classique, aucun courant ne peut traverser une barrière isolante. Cependant, selon les lois de la mécanique quantique, il existe une probabilité non nulle (supérieure à zéro) qu'un électron d'un côté de la barrière atteigne l'autre côté (voir effet tunnel quantique). L'application d'une différence de tension sur la jonction, permet d'établir un courant par effet tunnel, en négligeant les effets supplémentaires, le courant de tunnel sera proportionnel à la différence de tension.
Électroniquement, une jonction NIN se comporte comme une résistance à résistivité constante, également appelée résistance ohmique. La résistance dépend exponentiellement de l'épaisseur de la barrière. Les épaisseurs typiques de barrière sont de l'ordre de un à plusieurs nanomètres.
De plus, un dispositif NIN acquiert une capacité finie. La barrière de potentiel, c'est-à-dire la couche isolante est également appelée diélectrique, dans ce contexte, la jonction tunnel NIN se comporte comme un condensateur.
En raison de la nature discrète de la charge électrique, le courant à travers une jonction tunnel est une série d'événements dans lesquels exactement un électron passe (tunnels) à travers la barrière de potentiel (nous négligeons le cotunneling, dans lequel deux électrons traversent simultanément). Ainsi, sous ces restrictions, le condensateur de jonction tunnel est chargé d'une seule charge élémentaire par l'électron tunnel, provoquant une tension , où est la charge élémentaire de et la capacité de la jonction. Si la capacité est très petite, la différence de tension peut être suffisamment importante pour empêcher un autre électron de traverser par effet tunnel. Le courant électrique est ensuite supprimé à de faibles tensions et la résistance du dispositif n'est plus constante. L'augmentation de la résistance différentielle autour d'une différence de potentiel de zéro s'appelle le blocage de Coulomb.
Observer un blocage de Coulomb
Pour observer un blocage de Coulomb, l'énergie de charge caractéristique (l'énergie nécessaire pour charger la jonction avec une charge élémentaire) doit être plus grande que l'énergie thermique des porteurs de charge. Cette condition nécessite une température suffisamment basse. Dans le passé, pour des capacités supérieures à 1 femtofarad ( farad), cela demandait une température inférieure à environ 1 kelvin. Cette plage de température est couramment atteinte par exemple par les réfrigérateurs 3He. Grâce à l'utilisation de points quantiques (Quantum dots) de seulement quelques nanomètres, le blocage de Coulomb a été observé au-dessus de la température de l'hélium liquide jusqu'à la température ambiante[5],[6].
Pour réaliser une jonction tunnel de géométrie plane, produisant une capacité de 1 femtofarad, en utilisant une couche d'oxyde de permittivité électrique de 10 farad par mètre et d'une épaisseur de 1 nanomètre, il faut créer des électrodes carrées d'une dimensions de 100 nanomètres. Cette gamme de dimensions est couramment atteinte par exemple par lithographie par faisceau d'électrons et par des technologies appropriées de transfert de motifs, comme la technique de Niemeyer-Dolan, également connue sous le nom de shadow evaporation technique. La fabrication de points quantiques selon des standards industriels a été réussie pour le silicium. Le processus CMOS permet la production à grande échelle de transistors à points quantiques pour un seul électron allant jusqu'à une taille de 20 nm x 20 nm[7].
Transistor à un électron (S.E.T. : Single Electron Transistor)
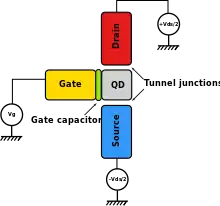
Le dispositif le plus simple dans lequel l'effet du blocage de Coulomb peut être observé est le transistor dit à un électron. Il se compose de deux électrodes connues sous le nom de drain et de source, reliées par des jonctions tunnel à une électrode commune avec une faible auto-capacité, connue sous le nom d'îlot. Le potentiel électrique de l'îlot peut être réglé par une troisième électrode, appelée porte, qui est couplée par capacité à l'îlot.
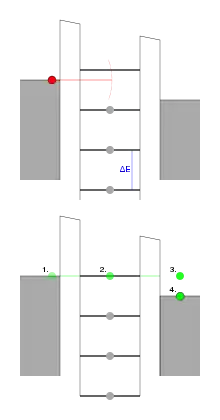
Dans l'état de blocage, aucun niveau d'énergie accessible par les électrons de la source ne permet l'occurrence d'un effet tunnel (voir figure en rouge) entre un électron de l'électrode de source vers un état inoccupé de l'îlot. Puisque tous les niveaux d'énergie de l'îlot avec des énergies inférieures à celle de l'électrode de source sont déjà occupés seuls des niveaux d'énergies supérieurs sont libres dans l'îlot.
Lorsqu'une tension positive est appliquée à l'électrode de porte, les niveaux d'énergie de l'électrode d'îlot sont abaissés. Ainsi maintenant, un électron de l'électrode de source (voir figure en vert 1.) peut pénétrer dans l'îlot (2.), occupant un niveau d'énergie précédemment vacant car anciennement trop élevé. À partir de là, il peut pénétrer dans l'électrode de drain (3.) où il se diffuse de façon inélastique et atteint le niveau de Fermi de l'électrode de drain (4.).
Les niveaux d'énergie de l'électrode de l'îlot sont espacés uniformément avec une séparation de . Ceci donne lieu à un auto-capacitance de l'îlot, défini comme.
Pour créer un blocage de Coulomb, il existe trois critères à satisfaire :
- La différence de tension doit être inférieure à la charge élémentaire divisée par l'auto-capacité de l'îlot: .
- L'énergie thermique dans le contact source plus l'énergie thermique dans l'îlot, c'est-à-dire , doit être inférieure à l'énergie de charge: . Autrement, l'électron pourrait passer de la source au drain uniquement par excitation thermique. Cela impose une limite sur la température maximal du dispositif.
- La résistance de la jonction tunnel, , doit être supérieur à . Cette condition dérive du principe d'incertitude de Heisenberg.
Thermomètre à blocage de Coulomb
Un thermomètre à blocage de Coulomb typique (CBT) est fabriqué à partir d'un réseau d'îlots métalliques, reliés les uns aux autres à travers une fine couche isolante. Une jonction tunnel se forme entre les îlots, et lorsqu'une tension est appliquée, les électrons peuvent traverser cette jonction par effet tunnel. La vitesse d’occurrence de transferts par effet tunnel et donc la conductivité de la jonction varient en fonction de l'énergie de charge des îlots et de l'énergie thermique du système.
Le thermomètre à blocage de Coulomb est un thermomètre primaire basé sur les caractéristiques de conductance électrique des réseaux de jonction tunnel. Le paramètre , la pleine largeur à la moitié du creux de conductance différentielle mesurée sur un réseau de N jonctions avec les constantes physiques fournit la température absolue.
Blocage ionique de Coulomb
Le blocage ionique de Coulomb[8] (ICB) est un cas particulier de blocage de Coulomb, apparaissant lors du transport électro-diffusif d'ions chargés à travers des nanopores artificiels[9] ou des canaux ioniques biologiques. L'ICB est largement similaire à son homologue électronique dans les points quantiques[1], mais présente des caractéristiques spécifiques définies par des valences z différentes des porteurs de charge (ions vs électrons) et par les différentes origines de transport (électro-diffusion classique vs tunnel quantique).
Dans le cas de l'ICB, l'espace de Coulomb est défini par l'auto-énergie diélectrique de l'ion entrant à l'intérieur du pore ou canal
et donc dépend de la valence des ions z. l'ICB apparaît fortement (), même à température ambiante, pour des ions avec , par exemple pour les ions .
Le blocage ionique de Coulomb a été récemment observé expérimentalement dans des pores sub-nanométriques [9].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Coulomb blockade » (voir la liste des auteurs).
- (en) D. V. Averin et K. K. Likharev, « Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel junctions », Journal of Low Temperature Physics, vol. 62, nos 3-4, , p. 345–373 (ISSN 0022-2291 et 1573-7357, DOI 10.1007/bf00683469, lire en ligne, consulté le )
- (en) Enrico Prati, « Valley Blockade Quantum Switching in Silicon Nanostructures », Journal of Nanoscience and Nanotechnology, vol. 11, no 10, , p. 8522–8526 (ISSN 1533-4880 et 1533-4899, DOI 10.1166/jnn.2011.4957, lire en ligne, consulté le )
- A. Crippa, M. L. V. Tagliaferri, D. Rotta et M. De Michielis, « Valley blockade and multielectron spin-valley Kondo effect in silicon », Physical Review B, vol. 92, no 3, (ISSN 1098-0121 et 1550-235X, DOI 10.1103/PhysRevB.92.035424, lire en ligne, consulté le )
- (en-GB) Xufeng Wang, Bhaskaran Muralidharan et Gerhard Klimeck, « Coulomb Blockade Simulation », nanoHUB (en), (DOI 10.4231/D3C24QP1W, lire en ligne, consulté le )
- O. D. D. Couto, J. Puebla, E. A. Chekhovich et I. J. Luxmoore, « Charge control in InP/(Ga,In)P single quantum dots embedded in Schottky diodes », Physical Review B, vol. 84, no 12, , p. 125301 (DOI 10.1103/PhysRevB.84.125301, lire en ligne, consulté le )
- (en) S. J. Shin, J. J. Lee, H. J. Kang et J. B. Choi, « Room-Temperature Charge Stability Modulated by Quantum Effects in a Nanoscale Silicon Island », Nano Letters, vol. 11, no 4, , p. 1591–1597 (ISSN 1530-6984 et 1530-6992, DOI 10.1021/nl1044692, lire en ligne, consulté le )
- (en) Enrico Prati, Marco De Michielis, Matteo Belli et Simone Cocco, « Few electron limit of n-type metal oxide semiconductor single electron transistors », Nanotechnology, vol. 23, no 21, , p. 215204 (ISSN 0957-4484 et 1361-6528, DOI 10.1088/0957-4484/23/21/215204, lire en ligne, consulté le )
- Matt Krems et Massimiliano Di Ventra, « Ionic Coulomb Blockade in Nanopores », Journal of physics. Condensed matter : an Institute of Physics journal, vol. 25, no 6, , p. 065101 (ISSN 0953-8984, PMID 23307655, PMCID PMC4324628, DOI 10.1088/0953-8984/25/6/065101, lire en ligne, consulté le )
- (en) Jiandong Feng, Ke Liu, Michael Graf et Dumitru Dumcenco, « Observation of ionic Coulomb blockade in nanopores », Nature Materials, vol. 15, no 8, , p. 850–855 (ISSN 1476-1122 et 1476-4660, DOI 10.1038/nmat4607, lire en ligne, consulté le )
- Portail de la physique
