Blossoming

Dans la Modélisation géométrique, le principe du Blossoming établit un lien entre les points d'une courbe et ses points des contrôle. Il était découvert en 1984 par Paul de Casteljau et publié par Lyle Ramshaw en 1987. Dans le cas d'arguments identiques (appelé la diagonale), le blossom (où floraison) détermine le point d'une courbe, dans le cas d'arguments consécutifs, un point de contrôle de cette courbe. En particulier, le blossoming relie les théories des courbes de Bézier et des courbes et surfaces B-spline, c'est-à-dire l'algorithme de Casteljau et l'algorithme de Boor.

Théorie générale

En mathématiques, particulièrement en Conception et fabrication assistées par ordinateur, on désigne comme Blossom ${\bf {b}}[t_{1},\dots ,t_{n}]$ du polynôme ${\bf {b}}(t)$ une fonction avec $n$ arguments, définie par trois propriétés:

Elle est symétrique dans ses arguments:

{\bf {b}}[t_{1},\dots ,t_{n}]={\bf {b}}{\big [}\pi (t_{1},\dots ,t_{n}){\big ]},\,

(où

\pi

est une permutation arbitraire de ses arguments).

Elle est multi-affine, donc affine dans chacun de ses arguments:

{\bf {b}}[\alpha r+\beta s,\dots ]=\alpha {\bf {b}}[r,\dots ]+\beta {\bf {b}}[s,\dots ],{\text{ mit }}\alpha +\beta =1.\,

Elle satisfait à la propriété de la diagonale:

{\bf {b}}[t,\dots ,t]={\bf {b}}(t).\,

Calcul

Comme toute polynôme symétrique rationelle se trouve dans $t_{1},\dots ,t_{n}$ peut être écrit comme un polynôme symétrique élémentaire

\sigma _{1}^{n}=t_{1}+t_{2}+\dots +t_{n}

\sigma _{2}^{n}=t_{1}t_{2}+t_{1}t_{3}+\dots +t_{2}t_{3}+\dots +t_{n-1}t_{n}

\dots

\sigma _{n}^{n}=t_{1}t_{2}t_{3}\dots t_{n}

nous pouvons algébriquement trouver le blossom du polynôme

{\bf {b}}(t)={\bf {a}}_{0}+\sum _{i=1}^{n}{\bf {a}}_{i}{\binom {n}{i}}t^{n}

comme

{\bf {b}}[t_{1},\dots ,t_{n}]={\bf {a}}_{0}+\sum _{i=1}^{n}{\bf {a}}_{i}\sigma _{i}^{n}

Exemple

Le blossom d'un polynôme quartique

{\begin{aligned}{\bf {x}}(t)\ &=\ {\bf {a}}_{0}{\binom {4}{0}}t^{0}+{\bf {a}}_{1}{\binom {4}{1}}t^{1}+{\bf {a}}_{2}{\binom {4}{2}}t^{2}+{\bf {a}}_{3}{\binom {4}{3}}t^{3}+{\bf {a}}_{4}{\binom {4}{4}}t^{4}\\&=\ {\bf {a}}_{0}+4{\bf {a}}_{1}t+6{\bf {a}}_{2}t^{2}+4{\bf {a}}_{3}t^{3}+{\bf {a}}_{4}t^{4}\end{aligned}}

est le polynôme symétrique et 4-affine

{\begin{aligned}{\bf {x}}[t_{1},\dots ,t_{4}]={\bf {a}}_{0}&+{\bf {a}}_{1}(t_{1}+t_{2}+t_{3}+t_{4})\\&+{\bf {a}}_{2}(t_{1}t_{2}+t_{1}t_{3}+t_{1}t_{4}+t_{2}t_{3}+t_{2}t_{4}+t_{3}t_{4})\\&+{\bf {a}}_{3}(t_{1}t_{2}t_{3}+t_{1}t_{2}t_{4}+t_{1}t_{3}t_{4}+t_{2}t_{3}t_{4})\\&+{\bf {a}}_{4}(t_{1}t_{2}t_{3}t_{4})\end{aligned}}

Applications

Blossoming d'une Courbe de Bézier

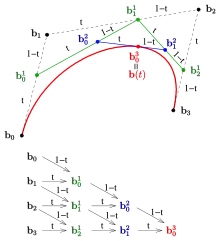
Algorithme de de Casteljau pour une courbe de Bézier du 3e degré

L'exemple d'une courbe de Bézier de degré $n=3$ montre clairement, comment le blossoming permet de déterminer à la fois les points de la courbe (dans l'image ${\bf {b}}_{0}$ et ${\bf {b}}_{3}$ ) et les points de contrôle (dans l'image ${\bf {b}}_{1}$ et ${\bf {b}}_{2}$ )

Le Blossom de la courbe de Bézier

{\begin{aligned}{\bf {b}}(t)\ &=\ \sum _{i=0}^{3}{\binom {3}{i}}t^{i}(1-t)^{3-i}{\bf {b}}_{i}\\&=\ (1-t)^{3}{\bf {b}}_{0}+3t(1-t)^{2}{\bf {b}}_{1}+3t^{2}(1-t){\bf {b}}_{2}+t^{3}{\bf {b}}_{3}\end{aligned}}

est le polynôme symétrique et tri-affine

{\begin{aligned}{\bf {b}}[t_{1},t_{2},t_{3}]&={\bf {b}}_{0}(1-t_{1})(1-t_{2})(1-t_{3})\\&+{\bf {b}}_{1}t_{1}(1-t_{2})(1-t_{3})\\&+{\bf {b}}_{2}t_{1}t_{2}(1-t_{3})\\&+{\bf {b}}_{3}(t_{1}t_{2}t_{3})\end{aligned}}

Si nous insérons des valeurs spéciales pour $t_{1},t_{2},t_{3}$ , on obtient

{\begin{aligned}{\bf {b}}_{000}:={\bf {b}}[0,0,0]&={\bf {b}}_{0}\\{\bf {b}}_{001}&={\bf {b}}_{1}\\{\bf {b}}_{011}&={\bf {b}}_{2}\\{\bf {b}}_{111}&={\bf {b}}_{3}\\\end{aligned}}

Plus encore, nous pouvons également calculer directement les points intermédiaires de l'algorithme de Casteljau sous forme de

{\begin{aligned}{\bf {b}}_{00t}:={\bf {b}}[0,0,t]&={\color {Green}{\bf {b}}_{0}^{1}}\\{\bf {b}}_{0t1}&={\color {Green}{\bf {b}}_{1}^{1}}\ &{\bf {b}}_{0tt}&={\color {Blue}{\bf {b}}_{0}^{2}}\\{\bf {b}}_{t11}&={\color {Green}{\bf {b}}_{2}^{1}}\ &{\bf {b}}_{tt1}&={\color {Blue}{\bf {b}}_{1}^{2}}\ &{\bf {b}}_{ttt}&={\color {Red}{\bf {b}}_{0}^{3}={\bf {b}}(t)}\\\end{aligned}}

Blossoming d'une Spline

Nous assemblons des courbes polynomiales par morceaux pour obtenir la courbe Spline.

{\begin{aligned}{\bf {s}}(u)\ &=\ \sum _{i=1}^{n}{\bf {c}}_{i}N_{i}^{n}(u)\ \end{aligned}}

avec B-splines $N_{i}^{n}$ . Si l'on met bout à bout les intervalles de paramètres sous-jacents, on obtient une séquence de nœuds $u_{1},u_{2},\dots ,u_{n}$ . Le blossoming sur les sous-intervalles conduit aux courbes de Bézier respectives ou aux points de contrôle de l'algorithme de Casteljau, soit par exemple

{\begin{aligned}{\bf {s}}_{333}:={\bf {s}}[u_{3},u_{3},u_{3}]&={\bf {b}}_{0}\\{\bf {s}}_{334}&={\bf {b}}_{1}\\{\bf {s}}_{344}&={\bf {b}}_{2}\\{\bf {s}}_{444}&={\bf {b}}_{3}\\\end{aligned}}

Le blossoming au-delà des sous-intervalles conduit aux points de contrôle de l'algorithme de de Boor:

{\begin{aligned}{\bf {s}}_{123}:={\bf {s}}[u_{1},u_{2},u_{3}]&={\bf {c}}_{0}\\{\bf {s}}_{234}&={\bf {c}}_{1}\\{\bf {s}}_{345}&={\bf {c}}_{2}\\{\bf {s}}_{456}&={\bf {c}}_{3}\\\end{aligned}}

Blossom et Osculante

Pour une courbe polynomiale ${\bf {x}}(t)$ de degré n, nous définissons

\Delta _{a}{\bf {x}}(t):={\bf {x}}(t)+{\bf {\dot {x}}}(t){\frac {a-t}{n}}

comme la première osculante de ${\bf {x}}(t)$ au nœud $a$ . C'est une courbe polynomiale de degré $n-1$ en $t$ et n'a en commun avec ${\bf {x}}(t)$ que le point ${\bf {x}}(a)$ où les courbes ont un contact d'ordre $n-1$ .

Pour $\Delta _{a}{bfx}$ , il est possible de déterminer une nouvelle osculante au nœud $b$ . C'est la deuxième oscillante de ${\bf {x}}$ aux nœuds $a$ et $b$ :

{\begin{aligned}\Delta _{ab}{\bf {x}}&=\ \Delta _{b}(\Delta _{a}{\bf {x}})\\&=\ \Delta _{b}{\bf {x}}+\Delta _{b}{\big (}{\bf {\dot {x}}}(t){\frac {a-t}{n}}{\big )}\\&=\ {\bf {x}}+{\bf {\dot {x}}}{\frac {(a-t)+(b-t)}{n}}+{\bf {\ddot {x}}}{\frac {(a-t)(b-t)}{n-1}}\end{aligned}}

Propriétés des Osculantes

Les Osculantes possèdent les propriétés suivantes:

Elles sont symétriques dans les nœuds:

\Delta _{ab}{\bf {x}}=\Delta _{ba}{\bf {x}}

Elles sont affines dans les nœuds: De $\ a=p\cdot (1-t)+q\cdot t$ découle

\Delta _{a}{\bf {x}}=(1-t)\cdot \Delta _{p}{\bf {x}}+t\cdot \Delta _{q}{\bf {x}}

Leur diagonale est identique à la courbe:

\Delta _{t}^{n}{\bf {x}}=\Delta _{t\dots t}{\bf {x}}={\bf {x}}(t)

Les osculants ont été introduits en 1886 par Stanislaus Jolles dans sa thèse d'habilitation. Dans le cas paramétrique, ils sont identiques aux blossoms de de Casteljau et Ramshaw et peuvent être facilement déduits par blossoming : Pour une courbe de Bézier cubique avec les points de contrôle ${\bf {b}}_{000},{\bf {b}}_{001},{\bf {b}}_{011},{\bf {b}}_{111}$ , l'osculante au nœud $t$ est définie par les points de contrôle de Bézier suivants : ${\bf {b}}_{00t},{\bf {b}}_{0t1},{\bf {b}}_{t11}$ .

Références

Stanislaus Jolles, Die Theorie der Osculanten und das Sehnensystem der Raumcurve IV. Ordnung II. Species; Ein Beitrag zur Theorie der rationalen Ebenenbüschel, Aachen, J. A. Mayer, 1886
Paul de Casteljau, Formes à Pôles, Hermès, coll. « Mathématiques et CAO », 1985
Paul de Casteljau, Mathematical methods in computer aided geometric design II, Academic Press Professional, Inc., 1992 (ISBN 978-0-12-460510-7), « POLynomials, POLar Forms, and InterPOLation »
Lyle Ramshaw, Blossoming: A Connect-the-Dots Approach to Splines, Digital Systems Research Center, 1987
Lyle Ramshaw, Blossoms are polar forms, Digital Systems Research Center, 1989
Gerald Farin, Curves and Surfaces for CAGD: A Practical Guide, Morgan Kaufmann, 2001, 5^e éd. (ISBN 1-55860-737-4)
Marie-Laurence Mazure, Blossoming stories, Numerical Algorithms, 2005, p. 257-288

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.