Bruit de phase

Dans le traitement du signal, le bruit de phase est la représentation dans le domaine fréquentiel des fluctuations aléatoires de la phase d'une forme d'onde. Il correspond aux écarts dans le domaine temporel par rapport à une périodicité parfaite ("gigue"). En général, les ingénieurs spécialisés en radiofréquences parlent du bruit de phase d'un oscillateur, alors que les ingénieurs spécialisés en systèmes numériques travaillent avec la gigue d'une horloge.

Bruit de phase mesuré par un analyseur de source de signal. L'analyseur montre la partie positive du bruit de phase. Sur cette image, on voit le bruit de phase de la porteuse principale, trois autres signaux et une "colline de bruit".
Un signal faible disparaît dans le bruit de phase d'un signal plus fort

Définitions

Historiquement, deux définitions contradictoires ont été utilisées pour le bruit de phase. Certains auteurs définissent le bruit de phase comme la densité spectrale de la phase d'un signal[1]. D'autres, par contre, font référence au spectre de phase (qui se couple avec le spectre d'amplitude) résultant de l'estimation spectrale du signal lui-même[2]. Les deux définitions donnent le même résultat à des fréquences de décalage suffisamment éloignées de la porteuse. Cependant, les deux définitions diffèrent pour des décalages rapprochés[3].

L'IEEE définit le bruit de phase comme ℒ(f) = Sφ(f)/2, où l'"instabilité de phase" Sφ(f) est la densité spectrale unilatérale de la déviation de phase d'un signal[4]. Bien que Sφ(f) soit une fonction unilatérale, elle représente "la densité spectrale à double bande latérale de la fluctuation de phase"[5]. Le symbole ℒ est appelé L script.

Contexte

Un oscillateur idéal générerait une onde sinusoïdale pure. Dans le domaine fréquentiel, cette onde serait représentée comme une paire de fonctions delta de Dirac (conjugués positifs et négatifs) à la fréquence de l'oscillateur. Tout le signal de puissance se trouverait ainsi à une fréquence unique. Tous les oscillateurs réels ont des composantes de bruit modulées en phase. Les composantes de bruit de phase répartissent la puissance d'un signal sur les fréquences adjacentes, ce qui entraîne des bandes latérales de bruit. Le bruit de phase de l'oscillateur comprend souvent un bruit de scintillation à basse fréquence. Il peut aussi inclure du bruit blanc.

Considérons le signal sans bruit suivant:

v(t) = Acos(2πf0t).

On ajoute un bruit de phase à ce signal en ajoutant au signal un processus stochastique représenté par φ, comme suit:

v(t) = Acos(2πf0t + φ(t)).

Le bruit de phase est un type de bruit cyclo-stationnaire. Il est étroitement lié à la gigue. Un type de bruit de phase particulièrement important est celui produit par les oscillateurs.

Le bruit de phase (ℒ(f)) est généralement exprimé en unités de dBc / Hz. Il représente la puissance de bruit par rapport à la porteuse contenue dans une bande passante d'un hertz centrée à des décalages spécifiques par rapport à la porteuse. Par exemple, un signal donné peut avoir un bruit de phase de -80 dBc/Hz avec un décalage de 10 kHz et −95 dBc/Hz avec un décalage de 100 kHz. Le bruit de phase peut être mesuré pour une bande latérale soit unique, soit double, mais l'IEEE a adopté comme définition la moitié de la densité de puissance spectrale de la double bande latérale.

Conversions de gigue

Le bruit de phase est parfois également mesuré et exprimé comme une puissance obtenue en intégrant ℒ(f) sur une certaine gamme de fréquences de décalage. Par exemple, le bruit de phase peut être de -40 dBc intégré sur la plage de 1 à 100 kHz. Ce bruit de phase intégré exprimé en degrés peut être converti en gigue, exprimée en secondes, à l'aide de la formule suivante:

En l'absence de bruit rose (bruit variant selon 1/f) dans une région où le bruit de phase affiche une pente de –20 dBc / décade (équation de Leeson), la gigue RMS du cycle peut être liée au bruit de phase par[6]:

De même:

Mesure

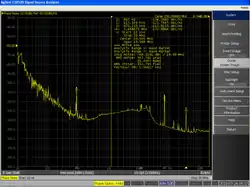
Le bruit de phase peut être mesuré à l'aide d'un analyseur de spectre si le bruit de phase de l'appareil testé est important par rapport à celui de l'oscillateur local de l'analyseur de spectre. Il faut cependant veiller à ce que les valeurs observées soient causées par le signal mesuré et non par le facteur de forme des filtres de l'analyseur de spectre. Une mesure basée sur un analyseur de spectre peut montrer la puissance du bruit de phase sur plusieurs ordres de grandeur en fréquence[7].

Les systèmes de mesure du bruit de phase sont une autre façon de mesurer le bruit de phase. Ces systèmes peuvent utiliser des références internes ou externes. Ils permettent la mesure du bruit résiduel (additif) ainsi que du bruit absolu. Ils peuvent également effectuer des mesures à faible bruit proches de la porteuse.

Pureté spectrale

La sortie sinusoïdale d'un oscillateur idéal forme une ligne unique dans le spectre de fréquences. Une pureté spectrale aussi parfaite n'est pas réalisable dans un oscillateur réel. L'étalement de la ligne spectrale causée par le bruit de phase doit être minimisé dans l'oscillateur local pour un récepteur superhétérodyne, car il enfreint l'objectif de restreindre la plage de fréquences du récepteur par des filtres dans l'amplificateur de fréquence intermédiaire.

Références
  1. J. Rutman et F.L. Walls, « Characterization of frequency stability in precision frequency sources », Proceedings of the IEEE, vol. 79, no 7,‎ , p. 952–960 (DOI 10.1109/5.84972, lire en ligne, consulté le )
  2. (en) Demir, A., Mehrotra, A. et Roychowdhury, J., « Phase noise in oscillators: a unifying theory and numerical methods for characterization », I.E.E.E. transactions on circuits and systems 1 : fundamental theory and applications, vol. 47, no 5,‎ , p. 655–674 (ISSN 1057-7122, potol.eecs.berkeley.edu/~jr/research/PDFs/2000-TCAS1-Demir-Mehrotra-Roychowdhury.pdf)
  3. Reza Navid, Christoph Jungemann, Thomas H. Lee et Robert W. Dutton, « Close-in phase noise in integrated oscillators », Noise in Communication, SPIE,‎ (DOI 10.1117/12.546818, lire en ligne, consulté le )
  4. 1139-1999 : IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology-Random Instabilities, IEEE, (ISBN 978-0-7381-1754-6 et 0-7381-1754-4, OCLC 1112400292, lire en ligne)
  5. (en) 1139-1999 - IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology-Random Instabilities, definition 2.7 stating ℒ(f) "is one half of the double-sideband spectral density of phase fluctuations." IEEE, 21 juillet 1999.
  6. « Jitter and Phase Noise in Circuits », dans Understanding Jitter and Phase Noise, Cambridge University Press (ISBN 978-1-107-18857-0, lire en ligne), p. 69–110
  7. « Phase Noise », dans Practical RF System Design, John Wiley & Sons, Inc. (ISBN 0-471-20023-9, lire en ligne), p. 245–272
  • Portail des télécommunications
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.