Centre de pression
En mécanique du solide, le centre de pression (CdP) est un point dynamique caractéristique d'un contact entre deux surfaces planes.
Définition et calcul
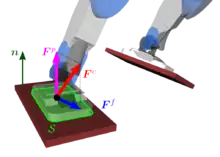
Considérons l'exemple ci-contre où le pied du robot humanoïde est en contact avec une surface plane. La résultante des forces de contact exercées par l'environnement sur le robot à travers la surface peut se décomposer en deux termes :
- la résultante des forces de pression, ainsi que
- la résultante des forces de frottement entre les deux surfaces. Ces forces sont tangentes à la surface ().
Ces résultantes sont la somme de forces infinitésimales exercées à chaque élément de surface de la surface de contact . En notant la pression en un point :
Comme le pied du robot ne peut pas pénétrer à l'intérieur du sol, la pression est toujours une quantité positive (on parle d'« unilatéralité des contacts »). Il en résulte l'existence d'un centre de pression, c'est-à-dire un point où le moment des forces de pression s'annule complètement (de même qu'au point d'application d'une force celle-ci n'exerce aucun moment). Celui-ci est donné par :
Les points et étant coplanaires, on obtient ainsi :
Par ailleurs, les forces de frottement étant parallèles à la surface de contact par définition, leur moment est aligné avec , de sorte que la relation ci-dessus s'écrit également
On utilise cette formule en pratique pour mesurer le CdP à l'aide d'un capteur de force.
Lien avec le ZMP
On reconnaît la formule du ZMP, appliquée cette fois-ci au torseur de contact (local) au lieu du torseur inertiel. Lorsqu'il n'y a qu'un seul contact, ces deux torseurs sont opposés en vertu de l'équation de Newton-Euler (voir l'article ZMP pour plus de détails), ce qui implique que le CdP et le ZMP coïncident[1].
Surface de sustentation
Tant que le contact avec la surface ne rompt pas, le centre de pression réside nécessairement à l'intérieur de la surface de contact. En effet, le moment des forces des contacts peut être réécrit :
La formule du CdP ci-dessus devient alors :
Ainsi, le CdP est la moyenne des points de contacts pondérée par les pressions qui y sont exercées. Lorsqu'il franchit le bord de la zone , le contact rompt et le pied du robot bascule. Pour éviter cela, les robots humanoïdes s'appliquent donc à maintenir leurs centres de pression à l'intérieur de ces zones pour chaque contact. Ce critère est une condition de non-basculement, et on parle alors de surface de sustentation pour désigner la zone .
Notes et références
- P. Sardain et G. Bessonnet, « Forces acting on a biped robot. Center of pressure-zero moment point », IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, vol. 34, , p. 630–637 (ISSN 1083-4427, DOI 10.1109/TSMCA.2004.832811, lire en ligne, consulté le )
- Portail de la physique