Advanced Encryption Standard

Advanced Encryption Standard ou AES (litt. « norme de chiffrement avancé »), aussi connu sous le nom de Rijndael, est un algorithme de chiffrement symétrique. Il remporta en octobre 2000 le concours AES, lancé en 1997 par le NIST et devint le nouveau standard de chiffrement pour les organisations du gouvernement des États-Unis. Il a été approuvé par la NSA (National Security Agency) dans sa suite B[1] des algorithmes cryptographiques. Il est actuellement le plus utilisé et le plus sûr[citation nécessaire].

Pour les articles homonymes, voir AES.

AES
Résumé
Concepteur(s) Joan Daemen, Vincent Rijmen
Première publication 2000
Dérivé de Rijndael, Square
Chiffrement(s) basé(s) sur cet algorithme Aucun
Caractéristiques
Taille(s) du bloc 128 bits
Longueur(s) de la clé 128, 192, 256 bits
Structure Réseau de substitution/permutation
Nombre de tours 10,12 ou 14 selon la taille de la clé

Meilleure cryptanalyse

Une attaque par clé apparentée casse 9 tours de AES-256. Une attaque par texte clair choisi casse 8 tours de AES-192 et 256, ou 7 tours de AES-128 (Ferguson et al, 2000).

Origine

Il est issu d'un appel à candidatures international lancé en janvier 1997 et ayant reçu 15 propositions. Parmi ces 15 algorithmes, 5 furent choisis pour une évaluation plus poussée en avril 1999 : MARS, RC6, Rijndael, Serpent, et Twofish. Au bout de cette évaluation, ce fut finalement le candidat Rijndael, du nom de ses deux concepteurs Joan Daemen et Vincent Rijmen (tous les deux de nationalité belge) qui a été choisi[2]. Ces deux experts en cryptographie étaient déjà les auteurs d'un autre algorithme : Square. AES est un sous-ensemble de Rijndael : il ne travaille qu'avec des blocs de 128 bits alors que Rijndael offre des tailles de blocs et de clefs qui sont des multiples de 32 (compris entre 128 et 256 bits).

Ce faisant, l'AES remplace le DES (choisi comme standard dans les années 1970) qui de nos jours devenait obsolète, car il utilisait des clefs de 56 bits seulement. L'AES a été adopté par le NIST (National Institute of Standards and Technology) en 2001. De plus, son utilisation est très pratique car il consomme peu de mémoire et n'étant pas basé sur un schéma de Feistel, sa complexité est moindre et il est plus facile à mettre en œuvre.

Fonctionnement

L'algorithme prend en entrée un bloc de 128 bits (16 octets), la clé fait 128, 192 ou 256 bits. Les 16 octets en entrée sont permutés selon une table définie au préalable. Ces octets sont ensuite placés dans une matrice de 4x4 éléments et ses lignes subissent une rotation vers la droite. L'incrément pour la rotation varie selon le numéro de la ligne. Une transformation linéaire est ensuite appliquée sur la matrice, elle consiste en la multiplication binaire de chaque élément de la matrice avec des polynômes issus d'une matrice auxiliaire, cette multiplication est soumise à des règles spéciales selon GF(28) (groupe de Galois ou corps fini). La transformation linéaire garantit une meilleure diffusion (propagation des bits dans la structure) sur plusieurs tours.

Finalement, un OU exclusif XOR entre la matrice et une autre matrice permet d'obtenir une matrice intermédiaire. Ces différentes opérations sont répétées plusieurs fois et définissent un « tour ». Pour une clé de 128, 192 ou 256, AES nécessite respectivement 10, 12 ou 14 tours.

Différence entre Rijndael et AES

La seule différence entre AES et Rijndael est l'ensemble des longueurs de bloc et la taille de clé. Rijndael est un bloc de chiffrement avec une longueur de bloc et une longueur de la clé variables. La longueur du bloc et la longueur de la clé peuvent être spécifiées indépendamment comme tout multiple de 32 bits, avec un minimum de 128 bits et un maximum de 256 bits. Il serait possible de définir des versions de Rijndael avec une la longueur du bloc ou la longueur de la clé, mais il ne semble pas que cela soit nécessaire actuellement[3].

L'AES fixe la longueur de bloc à 128 bits et prend en charge les longueurs de clé de 128, 192 ou 256 bits seulement. Les longueurs de bloc et de clé supplémentaires dans Rijndael ne sont pas évaluées dans le cadre du processus de sélection de l'AES, et par conséquent ils ne sont pas adoptés dans la norme FIPS actuelle[3].

Algorithme

Algorithme haut niveau pour le chiffrement avec Rijndael[3]:

procedure Rijndael(State,Cipherkey)
    KeyExpansion(CipherKey,ExpandedKey)
    AddRoundKey(State,ExpandedKey[0])
    for i = 1 to Nr − 1 do
        Round(State,ExpandedKey[i])
    end for
    FinalRound(State,ExpandedKey[Nr])
end procedure

Les tours de transformation de Rijndael[3]:

procedure Round(State,ExpandedKey[i])
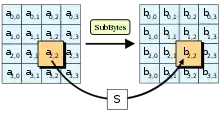
    SubBytes(State);
    ShiftRows(State);
    MixColumns(State);
    AddRoundKey(State,ExpandedKey[i]);
end procedure
procedure FinalRound(State,ExpandedKey[Nr])
    SubBytes(State);
    ShiftRows(State);
    AddRoundKey(State,ExpandedKey[Nr]);
end procedure

Attaques

Rijndael a été conçu de façon à résister aux méthodes classiques en particulier la cryptanalyse linéaire et la cryptanalyse différentielle. Le nombre de tours de l'AES est calculé en fonction de la taille de la clef pour que chacune de ces deux attaques (linéaire et différentielle) ne soit pas plus efficace qu'une attaque par force brute.

L'AES n'a pour l'instant pas été cassé, même théoriquement, au sens où il n'existe pas d'attaque significativement plus efficace que la recherche exhaustive quand le chiffrement est correctement utilisé.

Attaques sur des versions simplifiées

Des attaques existent sur des versions simplifiées d'AES. Niels Ferguson et son équipe ont proposé en 2000 une attaque sur une version à 7 tours de l'AES 128 bits. Une attaque similaire casse un AES de 192 ou 256 bits contenant 8 tours. Un AES de 256 bits peut être cassé s'il est réduit à 9 tours avec une contrainte supplémentaire. En effet, cette dernière attaque repose sur le principe des « related-keys » (clés apparentées). Dans une telle attaque, la clé demeure secrète mais l'attaquant peut spécifier des transformations sur la clé et chiffrer des textes à sa guise. Il peut donc légèrement modifier la clé et regarder comment la sortie de l'AES se comporte.

Attaques sur la version complète

La simplicité algébrique de l'AES a été mise en avant, par exemple en 2001 par Niels Ferguson, comme une potentielle faiblesse[4]. Elle n'a cependant pu être exploitée jusqu'à présent. En 2002 Nicolas Courtois et Josef Pieprzyk avaient présenté une attaque algébrique théorique l'attaque XSL, dont ils estimaient qu'elle était plus efficace que l'attaque par force brute, mais cela a été infirmé par des travaux ultérieurs[5].

En 2011, des chercheurs de Microsoft publient une attaque sur la version complète d'AES[6]. Cette attaque permet de trouver la clef d'AES-128 en opérations (contre pour une attaque par force brute, soit presque 4 fois plus rapide que cette dernière). La même attaque s'applique à une version simplifiée (à 8 tours) d'AES-128, réduisant la complexité de l'attaque à . Cette attaque, fondée sur une amélioration de l'attaque par rencontre au milieu, reste impraticable.

Recommandations de la NSA

Le gouvernement américain a annoncé en juin 2003 à propos de l'algorithme AES (suivant une analyse de la NSA) :

« L'architecture et la longueur de toutes les tailles de clés de l'algorithme AES (128, 192 et 256) sont suffisantes pour protéger des documents classifiés jusqu'au niveau « SECRET ». Le niveau « TOP SECRET » nécessite des clés de 192 ou 256 bits. L'implémentation de l'AES dans des produits destinés à la protection des systèmes et/ou documents liés à la sécurité nationale doit faire l'objet d'une analyse et d'une certification par la NSA avant leur acquisition et leur utilisation »

— paragraphe (6) de la dépêche originale[7]

Attaques par canal auxiliaire

Les attaques par canal auxiliaire exploitent les faiblesses du système implémentant l'algorithme de chiffrement et ne le visent donc pas directement. Il existe plusieurs attaques connues de ce type pour l'AES.

En , Daniel J. Bernstein a publié une attaque temporelle utilisée pour casser une clé AES sur un serveur spécifique tournant avec OpenSSL.

En , Endre Bangerter, David Gullasch et Stephan Krenn ont publié un article décrivant la récupération d'une clé secrète AES-128 quasiment en temps réel qui fonctionne sur certaines implémentations. Comme les précédentes attaques de ce type, elle nécessite de lancer un programme sur la machine qui effectue le chiffrement.

Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Advanced Encryption Standard » (voir la liste des auteurs).
  1. (en) « Suite B Cryptography »
  2. (en) James Nechvatal, Elaine Barker, Lawrence Bassham, William Burr, Morris Dworkin, James Foti, Edward Roback, « Report on the Development of the Advanced Encryption Standard (AES) », sur csrc.nist.gov, National Institute of Standards and Technology, (consulté le )
  3. Joan Daemen, The design of Rijndael : the Advanced Encryption Standard (AES), (ISBN 978-3-662-60769-5 et 3-662-60769-7, OCLC 1155884098, lire en ligne)
  4. (en) Niels Ferguson, Richard Schroeppel et Doug Whiting (2001) « A Simple Algebraic Representation of Rijndael » Selected Areas in Cryptography: 103–111 p., Springer Berlin Heidelberg.
  5. (en) C. Cid, G. Leurent, « An Analysis of the XSL Algorithm », LNCS, vol. 3788,‎ , p. 333–335 (DOI 10.1007/11593447, lire en ligne [PDF])
  6. (en) Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger, « Biclique Cryptanalysis of the Full AES »,
  7. https://web.archive.org/web/20070927035010/http://www.cnss.gov/Assets/pdf/cnssp_15_fs.pdf

Annexes

Articles connexes

Liens externes
  • Portail de la cryptologie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.